
Szamoszi Püthagorasz (570-495 k.-495 Kr.e.)
Élettörténet – Ki volt Püthagorasz
Néha azt állítják, hogy a tiszta matematikát Püthagorasznak köszönhetjük, és gyakran nevezik őt az első “igazi” matematikusnak. De bár hozzájárulása egyértelműen fontos volt, mégis ellentmondásos alak maradt.
Maga nem hagyott hátra matematikai írásokat, és amit a püthagoraszi gondolkodásról tudunk, annak nagy részét Philolausz és más későbbi püthagoraszi tudósok írásaiból ismerjük. Sőt, egyáltalán nem világos, hogy a neki tulajdonított tételek közül sok (vagy egyáltalán bármelyik) tételt valóban személyesen Püthagorasz vagy követői oldották-e meg.
A Kr. e. 530 körül a dél-itáliai Crotonban általa alapított iskola egy meglehetősen bizarr püthagoreus szekta magja volt. Bár a püthagoreus gondolkodást nagyrészt a matematika uralta, mélységesen misztikus is volt, és Püthagorasz kvázi-vallásos filozófiáját, szigorú vegetarianizmusát, közösségi életmódját, titkos rítusait és furcsa szabályait az iskolája minden tagjára ráerőltette (beleértve a bizarr és látszólag véletlenszerű rendeleteket arról, hogy soha ne vizeljen a nap felé, soha ne vegyen feleségül arany ékszert viselő nőt, soha ne menjen el egy utcán fekvő szamár mellett, soha ne egyen vagy akár csak érintsen fekete lóbabot, stb.
A tagok “matematikoi”-ra (vagy “tanulókra”) oszlottak, akik kiterjesztették és továbbfejlesztették azt a matematikai és tudományosabb munkát, amelyet maga Püthagorasz kezdett el, és az “akousmatikoi”-ra (vagy “hallgatókra”), akik tanításainak vallásosabb és rituálisabb aspektusaira összpontosítottak. A két csoport között mindig volt némi súrlódás, és végül a szekta heves helyi harcokba keveredett, majd végül feloszlott. A püthagoreusok titkolózása és kizárólagossága ellen felerősödött a harag, és i. e. 460-ban az összes találkozóhelyüket felgyújtották és elpusztították, és csak Krótonban legalább 50 tagjukat megölték.
Püthagorasz iskolájának legfőbb diktuma a “Minden a szám” vagy “Isten a szám” volt, és a püthagoreusok gyakorlatilag egyfajta számmisztikát vagy számimádatot gyakoroltak, és minden számnak saját karaktert és jelentést tulajdonítottak. Például az egyes szám volt minden szám generátora; a kettes a véleményt, a hármas a harmóniát, a négyes az igazságosságot, az ötös a házasságot, a hatos a teremtést, a hetes a hét bolygót vagy “vándorcsillagot” stb. jelentette. A páratlan számokat női, a páros számokat pedig férfi számoknak tekintették.
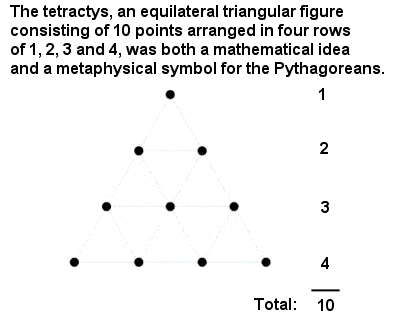
A püthagoreus Tetraktisz
A legszentebb szám a “Tetraktisz” vagy tíz, az egy, kettő, három és négy összegéből álló háromszögszám volt. A püthagoreusok szellemi teljesítményének nagy elismerése, hogy a 10-es szám különleges helyét egy elvont matematikai érvelésből vezették le, nem pedig valami olyan hétköznapi dologból, mint a két kéz ujjainak megszámlálása.
Mindenesetre Püthagorasz és iskolája – valamint az ókori Görögország maroknyi más matematikusa – nagyrészt felelős volt egy, az addigiaknál szigorúbb matematika bevezetéséért, amely axiómák és logika segítségével az első elvekből építkezett. Püthagorasz előtt például a geometria csupán empirikus mérésekből levezetett szabályok gyűjteménye volt.
Püthagorasz felfedezte, hogy felépíthető egy teljes matematikai rendszer, ahol a geometriai elemek megfeleltek a számoknak, és ahol az egész számok és arányaik voltak az egyetlenek, amik szükségesek egy teljes logikai és igazságrendszer létrehozásához.
A Pitagorasz-tétel
Főként a Pitagorasz-tételként (vagy Pitagorasz-tételként) ismertté vált tétel miatt emlékeznek rá: bármely derékszögű háromszög esetében a hipotenzus (a leghosszabb oldal, a derékszöggel szemben) hosszának négyzete egyenlő a másik két oldal (vagy “láb”) négyzetének összegével.
Egyenletként leírva: a2 + b2 = c2.
Azt azonban Pitagorasz és követői nem vették észre, hogy ez bármilyen alakzatra is érvényes: így az ötszög hipotenzuson lévő területe egyenlő a másik két oldalon lévő ötszögek összegével, ahogyan ez egy félkör vagy bármely más szabályos (vagy akár szabálytalan( alakzat esetében is így van.
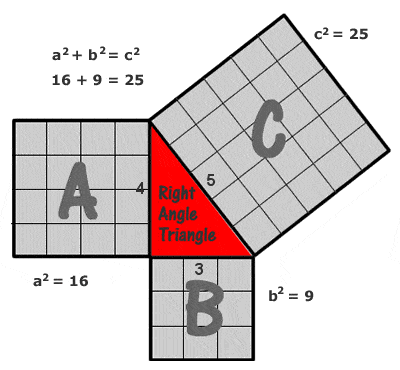
Püthagorasz (Pitagorasz) tétele
A legegyszerűbb és leggyakrabban idézett példa a Pitagorasz-háromszögre az, amelynek oldalai 3, 4 és 5 egységnyi (32 + 42 = 52, amint az látható, ha mindkét oldalra egységnyi négyzetekből álló rácsot rajzolunk, mint a jobb oldali ábrán), de potenciálisan végtelen számú más egész számú “Pitagorasz-háromszög létezik, kezdve az (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41) stb. oldalakkal. Meg kell azonban jegyezni, hogy a (6, 8, 10) nem az úgynevezett “primitív” püthagoraszi hármas, mert ez csak a (3, 4, 5) többszöröse.
Püthagorasz tétele és a derékszögű háromszögek tulajdonságai az alapvető számtan és geometria után a legősibb és legelterjedtebb matematikai fejlesztésnek tűnik, és már a legősibb, több mint ezer évvel korábbi babiloni és egyiptomi matematikai szövegekben is szóba került. Az egyik legegyszerűbb bizonyítás az ókori Kínából származik, és valószínűleg jóval Pitagorasz születése előttről származik. Pitagorasz volt azonban az, aki a tétel végleges formáját adta, bár nem világos, hogy maga Pitagorasz bizonyította-e véglegesen, vagy csak leírta. Akárhogy is, ez lett az egyik legismertebb matematikai tétel, és ma már 400 különböző bizonyítás létezik, némelyik geometriai, némelyik algebrai, némelyik fejlett differenciálegyenletekkel stb.
Akkor azonban kiderült, hogy nem egész számú megoldások is lehetségesek, így például az 1, 1 és √2 oldalú egyenlő szárú háromszögnek derékszöge is van, amint azt a babilóniaiak már évszázadokkal korábban felfedezték. Amikor azonban Püthagorasz tanítványa, Hippaszosz megpróbálta kiszámítani √2 értékét, azt tapasztalta, hogy azt nem lehet törtként kifejezni, ami egy teljesen új számvilág, az irracionális számok (az egész számok egyszerű törteként ki nem fejezhető számok) lehetséges létezésére utalt. Ez a felfedezés meglehetősen összetörte a Püthagorasz és követői által felépített elegáns matematikai világot, és egy olyan szám létezése, amelyet nem lehetett Isten két teremtményének hányadosaként kifejezni (így gondoltak az egész számokra), veszélyeztette a szekta egész hitrendszerét.
A szegény Hippaszoszt a jelek szerint megfojtották a titkolózó püthagoreusok, amiért ezt a fontos felfedezést a külvilág felé közvetítette. De az, hogy az egész számok istenségének eszméjét felváltotta a kontinuum gazdagabb fogalma, lényeges fejlemény volt a matematikában. Ez jelentette a görög geometria igazi születését, amely vonalakkal, síkokkal és szögekkel foglalkozik, amelyek mind folytonosak és nem diszkrétek.
A geometriában elért egyéb eredményei mellett Püthagorasz (vagy legalábbis követői, a püthagoreusok) azt is felismerte, hogy egy háromszög szögeinek összege két derékszöggel (180°) egyenlő, és valószínűleg azt az általánosítást is, amely szerint egy n oldalú sokszög belső szögeinek összege (2n – 4) derékszöggel egyenlő, és hogy külső szögeinek összege 4 derékszöggel egyenlő. Képesek voltak adott területű alakzatokat konstruálni, és egyszerű geometriai algebrát alkalmazni, például az olyan egyenleteket, mint a(a – x) = x2, geometriai eszközökkel megoldani.
A püthagoreusok a számelmélet alapjait is megteremtették a háromszög-, négyzet- és a tökéletes számok (olyan számok, amelyek osztóik összege) vizsgálatával. Felfedezték a négyzetszámok számos új tulajdonságát, például azt, hogy egy n szám négyzete egyenlő az első n páratlan szám összegével (pl. 42 = 16 = 1 + 3 + 5 + 7). Felfedezték a 220 és a 284-es számok legalább első amikábilis számpárját is (amikábilis számok olyan számpárok, amelyek esetében az egyik szám osztóinak összege egyenlő a másik számmal, pl. a 220 helyes osztói 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 és 110, amelyek összege 284; a 284 helyes osztói pedig 1, 2, 4, 71 és 142, amelyek összege 220).
Zeneelmélet
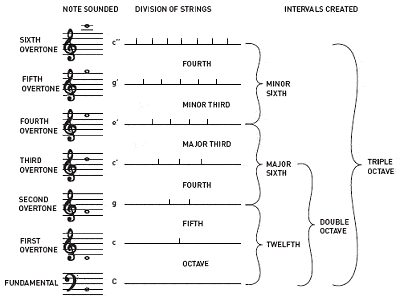
Pythagorasnak tulajdonítják a harmonikus zenei hangok közötti arányok felfedezését
Pythagorasnak tulajdonítják annak felfedezését is, hogy a harmonikus zenei hangok közötti intervallumok mindig egész számok arányai. Például egy gitárhúr fél hosszának megszólaltatása ugyanazt a hangot adja, mint a nyitott húr, de egy oktávval feljebb; egy harmad hosszának megszólaltatása más, de harmonikus hangot ad; stb.
A nem egész számarányok viszont hajlamosak disszonáns hangokat adni. Püthagorasz így írta le az első négy felhangot, amelyek létrehozzák azokat a közös intervallumokat, amelyek a zenei harmónia elsődleges építőköveivé váltak: az oktáv (1:1), a tökéletes kvint (3:2), a tökéletes kvart (4:3) és a nagy terc (5:4). A 12 hangú kromatikus skála hangolásának legrégebbi módja a püthagoraszi hangolás néven ismert, és tökéletes kvintek halmazán alapul, amelyek mindegyike 3:2 arányban van hangolva.
A misztikus Püthagoraszt annyira izgatta ez a felfedezés, hogy meggyőződése lett, hogy az egész világegyetem számokon alapul, és hogy a bolygók és csillagok matematikai egyenletek szerint mozognak, amelyek megfelelnek a zenei hangoknak, és így egyfajta szimfónia, a “Musical Universalis” vagy “Szférák zenéje” keletkezett.
| << Vissza a görög matematikához | Előre Platónhoz >> |
.
