A Bayes-féle információs kritérium (BIC) a modellek véges halmazából történő modellkiválasztás kritériuma. Részben a valószínűségi függvényen alapul, és szoros kapcsolatban áll az Akaike információs kritériummal (AIC).
Modellek illesztésekor lehetőség van a valószínűség növelésére paraméterek hozzáadásával, de ez túlillesztéshez vezethet. A BIC ezt a problémát úgy oldja meg, hogy büntetőtermet vezet be a modellben szereplő paraméterek számának függvényében. A büntető kifejezés a BIC-ben nagyobb, mint az AIC-ben.
A BIC-t széles körben használják modellazonosításra idősorok és lineáris regresszió esetén. Elég széles körben alkalmazható azonban a maximális valószínűségen alapuló modellek bármely halmazára.
Matematikailag a BIC a következőképpen határozható meg.
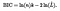

Alkalmazás & Értelmezés:
A modellek a megfelelő BIC-értékek segítségével tesztelhetők. Az alacsonyabb BIC-érték alacsonyabb büntetőfeltételekre utal, tehát jobb modellre.
Az AIC-statisztika is olvasható.
Bár ez a két mérték eltérő szemszögből származik, mégis szorosan összefüggnek egymással. Látszólag az egyetlen különbség az, hogy a BIC figyelembe veszi a megfigyelések számát a képletben, amit az AIC nem.
A BIC ugyan mindig magasabb, mint az AIC, de alacsonyabb e két mérték értéke, jobb a modell.
Gyakorlati adathalmaz:
Látogasson el az Analyttica TreasureHunt nevű adattudományi és analitikai platformunkra, hogy valódi adathalmazokon gyakorolhasson.
Még olvassa el a következőket:
Konkordanciaellenőrzés.
Kernel Filter.
k-Means Clustering.
.
