Ebben a részben megismerkedünk a halmazműveletekkel és jelölésekkel, hogy ezeket a fogalmakat alkalmazni tudjuk mind a számolási, mind a valószínűségi problémákra. Néhány fogalom meghatározásával kezdjük.
A halmaz objektumok gyűjteménye, és tagjait a halmaz elemeinek nevezzük. A halmazt nagybetűkkel nevezzük el, tagjait pedig szögletes zárójelek közé zárjuk. Tegyük fel, hogy fel kell sorolnunk a sakk-klub tagjait. A következő halmazjelölést használjuk:
C ={Ken, Bob, Tran, Shanti, Eric}
At olyan halmazt, amelynek nincsenek tagjai, üres halmaznak nevezzük. Az üres halmazt az Ø szimbólummal jelöljük.
Két halmaz akkor egyenlő, ha ugyanazok az elemeik.
A halmaz A egy B halmaz részhalmaza, ha A minden tagja egyben B tagja is.
Tegyük fel, hogy C = {Al, Bob, Chris, David, Ed} és A = {Bob, David}. Akkor A C részhalmaza, amit 
-nak írunk.
Minden halmaz önmagának részhalmaza, és az üres halmaz minden halmaz részhalmaza.
Két halmaz uniója
Legyen A és B két halmaz, akkor A és B uniója, amit 
-nak írunk, az összes olyan elem halmaza, amely vagy A-ban vagy B-ben, vagy A-ban és B-ben egyaránt benne van.
Két halmaz metszete
Legyen A és B két halmaz, akkor A és B metszete, írva 
, mindazon elemek halmaza, amelyek mind az A, mind a B halmazban közösek.
Az U univerzális halmaz az összes vizsgált elemet tartalmazó halmaz.
egy halmaz komplementje
Legyen A bármilyen halmaz, akkor az A halmaz komplementje, amelyet 
-ként írunk, az U univerzális halmaz azon elemeiből álló halmaz, amelyek nem szerepelnek A-ban.
Diszjunkt halmazok
Két A és B halmazt diszjunkt halmaznak nevezünk, ha metszéspontjuk üres halmaz.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {narancs, zöld, indigó, lila}A jobb megértés érdekében tegyük fel, hogy az U univerzális halmaz a spektrum színeit, P pedig az alapszíneket képviseli, akkor a spektrum azon színeit képviseli, amelyek nem alapszínek.
.
= {piros, sárga, kék, zöld}
= {narancs, indigó, lila}
= {piros, sárga, kék, ibolya} = {lila}Venn-diagramok
Most Venn-diagramokkal szemléltetjük a halmazok közötti kapcsolatokat. Az 1800-as évek végén egy John Venn nevű angol logikus kifejlesztett egy módszert a halmazok közötti kapcsolatok ábrázolására. Ezeket a kapcsolatokat diagramokkal ábrázolta, amelyeket ma Venn-diagramokként ismerünk. A Venn-diagram egy halmazt egy kör belsejeként ábrázol. Gyakran két vagy több kört egy téglalapba zárnak, ahol a téglalap az univerzális halmazt jelképezi. Egy halmaz metszetének vagy uniójának szemléltetése egyszerű. Ebben a részben a Venn-diagramokat elsősorban különböző halmazok rendezésére és objektumok megszámlálására fogjuk használni.
|
(a) |
(b) |
(c) |
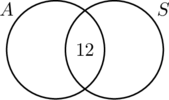
Mert 30 ember automata váltós autót vezetett, az A körnek 30 elemet kell tartalmaznia. Ez azt jelenti, hogy x + 12 = 30, vagy x = 18. Hasonlóképpen, mivel 20 ember normál sebességváltós autót vezetett, a B körnek 20 elemet kell tartalmaznia, vagy y +12 = 20, ami viszont y = 8.
Most, hogy minden információ rendeződött, könnyen leolvasható az ábráról, hogy 18 ember csak automata sebességváltós autót vezetett, 12 ember mindkét autótípust vezette, és 8 ember csak normál sebességváltós autót vezetett. Tehát 18 + 12 + 8 = 38 ember vett részt a felmérésben.
|
(a) |
(b) |
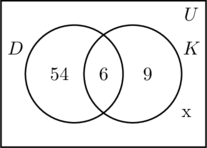
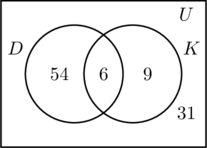
A D és K halmazokhoz tartozó három régiót ugyanúgy kitöltjük, mint korábban. Mivel a felmérésben 100 ember vett részt, az U univerzális halmazt reprezentáló téglalapnak 100 objektumot kell tartalmaznia. Jelölje x azokat az embereket az univerzális halmazban, akik sem a D, sem a K halmazban nem szerepelnek. 54 + 6 + 9 + x = 100, vagyis x = 31.
Ez azt jelenti, hogy a felmérésben 31 olyan ember vett részt, aki egyik helyen sem járt.
- 50 kocog, 30 úszik és 35 kerékpározik
- 14 kocog és úszik
- 7 úszik és kerékpározik
- 9 kocog és kerékpározik
- 3 ember mindhárom tevékenységben részt vesz
Megoldás
|
(a) |
(b) |
(c) |
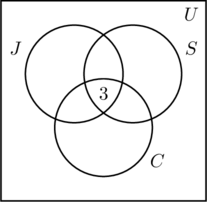
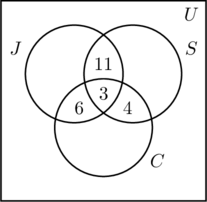
Az (a) ábra legbelső régiójába egy 3-ast teszünk, mert ez jelzi azoknak a számát, akik mindhárom tevékenységben részt vesznek. Ezután kiszámítjuk az x, y és z értékeket.
- Mivel 14 ember kocog és úszik, x +3 = 14, vagy x = 11.
- Az a tény, hogy 9 ember kocog és kerékpározik, azt eredményezi, hogy y + 3 = 9, vagy y = 6.
- Mivel 7 ember úszik és kerékpározik, z + 3 = 7, vagy z = 4.
- Ezt az információt a (b) ábra ábrázolja.
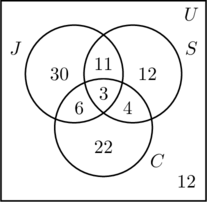
- Mivel 50 ember kocog, m + 11 + 6 + 3 = 50, vagy m = 30.
- 30 ember úszik, tehát n + 11 + 4 + 3 = 30, vagy n = 12.
- 35 ember kerékpározik, tehát p + 6 + 4 + 3 = 35, vagy p = 22.
- A három halmaz összes bejegyzését összeadva 88-as összeget kapunk. Mivel 100 embert kérdeztek meg, az univerzális halmazon belüli, de mindhárom halmazon kívüli szám 100 – 88, azaz 12.
- A c) ábrán az információk rendeződnek, és a kérdések könnyen megválaszolhatók.
GYakorlati kérdések
1. Legyen az univerzális halmaz U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h} és W = {a, c, e, g, i}. Sorolja fel a következő halmazok tagjait:
a. 
b. 
2. Tekintsük a következő halmazokat: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, influenza, Norovírus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovírus, Shigella} és C = {SARS, Listeria, tuberkulózis, H5N1, Salmonella, HIV, COVID-19}. Sorolja fel a következő halmazok tagjait:
a. 
b. 
3. Egy sportolók körében végzett felmérésből kiderült, hogy kisebb fájdalmaikra 30-an aszpirint, 50-en ibuprofent, 15-en pedig mindkettőt használták. A megkérdezett sportolók mindegyike használta a két fájdalomcsillapító közül legalább az egyiket. Hány sportolót kérdeztek meg?
4. Egy 150 középiskolás diák körében végzett vizsgálat szerint 25-en számoltak be korábbi agyrázkódásról vagy fejsérülésről, 52-en mentális betegségről, 15-en pedig mindkettőről. Hány diák nem számolt be egyik eredményről sem?
5. A Ryerson Egyetem 100 diákja körében végzett felmérés szerint 50-en előfizetnek a Netflixre, 40-en az Amazon Prime-ra, 30-an pedig a Disney+-ra. Közülük 15-en a Netflixre és az Amazon Prime-ra is előfizetnek, 10-en az Amazon Prime-ra és a Disney+-ra is, 10-en a Netflixre és a Disney+-ra is, 5-en pedig mindhárom előfizetési szolgáltatásra. Rajzoljon egy Venn-diagramot, és határozza meg a következőket:
a. Az Amazon Prime-ra előfizető, de a másik két streaming szolgáltatásra nem előfizető diákok száma.
b. A Netflixre vagy az Amazon Prime-ra előfizető, de a Disney+-ra nem előfizető diákok száma.
c. Azon diákok száma, akik egyik szolgáltatásra sem fizetnek elő.