Articles

Fizika

admin0

Tanulmányi célok

A fejezet végére képes leszel:

  • leírni egy tipikus fotoelektromos hatásos kísérletet.
  • Meghatározni az egy energiájú vagy hullámhosszú fotonok által kilökött fotoelektronok maximális kinetikus energiáját, ha adott a fotoelektronok maximális kinetikus energiája egy másik fotonenergia vagy hullámhossz esetén.

Amikor a fény anyagokra esik, elektronokat tud kilökni belőlük. Ezt nevezzük fotoelektromos hatásnak, ami azt jelenti, hogy a fény (fotó) elektromosságot termel. A fotoelektromos hatás egyik gyakori felhasználási területe a fénymérők, például azok, amelyek a különböző típusú fényképezőgépek automatikus íriszét állítják be. Hasonló módon egy másik felhasználási terület a napelemek, amelyek valószínűleg a számológépedben vannak, vagy már láttad őket egy tetőn vagy egy út menti táblán. Ezek a fotoelektromos hatást használják ki, hogy a fényt elektromos árammá alakítsák a különböző eszközök működtetéséhez.

1. ábra. A fotoelektromos hatás úgy figyelhető meg, hogy ebben a kiürített csőben a fémlemezre fény esik. A fény által kilökött elektronokat a gyűjtőszálon összegyűjtik, és áramként mérik. A kollektorhuzal és a lemez közötti késleltető feszültséget ezután úgy lehet beállítani, hogy a kilökött elektronok energiáját meg lehessen határozni. Ha például elég negatív, akkor nem jutnak elektronok a huzalra. (hitel: P.P. Urone)

Ez a hatás több mint egy évszázada ismert, és az 1. ábrán láthatóhoz hasonló eszközzel tanulmányozható. Ez az ábra egy evakuált csövet ábrázol egy fémlemezzel és egy kollektorhuzallal, amelyeket egy változó feszültségforrás köt össze, úgy, hogy a kollektor negatívabb, mint a lemez. Amikor fény (vagy más EM-sugárzás) éri a lemezt az evakuált csőben, az elektronokat lökhet ki. Ha az elektronok energiája elektronvoltban (eV) kifejezve nagyobb, mint a lemez és a vezeték közötti potenciálkülönbség voltban kifejezve, akkor néhány elektron összegyűlik a vezetéken. Mivel az elektronok energiája eV-ban eV, ahol q az elektrontöltés és V a potenciálkülönbség, az elektronok energiája a huzal és a lemez közötti késleltető feszültség beállításával mérhető. Az a feszültség, amely megakadályozza, hogy az elektronok elérjék a huzalt, egyenlő az eV-ban kifejezett energiával. Például, ha -3,00 V alig állítja meg az elektronokat, akkor az energiájuk 3,00 eV. A kilökött elektronok számát a huzal és a lemez közötti áram mérésével lehet meghatározni. Minél több a fény, annál több az elektron; egy kis áramkörrel ez a készülék fénymérőként is használható.

Az igazán fontos a fotoelektromos effektussal kapcsolatban az, amit Albert Einstein levont belőle. Einstein felismerte, hogy a fotoelektromos effektusnak több olyan jellemzője is van, amely csak akkor magyarázható, ha az EM-sugárzás maga is kvantált: az EM-hullám látszólag folyamatos energiaáramlása valójában fotonoknak nevezett energiakvantumokból áll. A fotoelektromos hatás magyarázatában Einstein meghatározta az EM-energia kvantált egységét vagy kvantumát, amelyet ma fotonnak nevezünk, és amelynek energiája arányos az EM-sugárzás frekvenciájával. Egyenlet formájában a foton energiájaE = hf, ahol E az f frekvenciájú foton energiája, h pedig a Planck-állandó. Ez a forradalmi elképzelés hasonlít a feketetest-oszcillátorok energiaállapotainak Planck-féle kvantálásához, de egészen más. Ez magának az EM-sugárzásnak a kvantálása. Az EM-hullámok fotonokból állnak, és nem folytonos, sima hullámok, ahogyan azt az optikáról szóló korábbi fejezetekben leírtuk. Energiájukat csomókban veszik fel és bocsátják ki, nem folyamatosan. Ez pontosan megfelel Plancknak a feketetest-oszcillátorok energiaszintjeinek kvantálásával, mivel ezek az oszcillátorok hf lépésekben növelik és csökkentik energiájukat az E = hf értékű fotonok elnyelésével és kibocsátásával. Ezt nem észleljük a szemünkkel, mert a közönséges fényforrásokban olyan sok foton van, hogy az egyes fotonok észrevétlenek maradnak. (Lásd a 2. ábrát.) A szöveg következő szakasza (A fotonenergiák és az elektromágneses spektrum) a fotonok, valamint néhány jellemzőjük és következményük tárgyalása. Egyelőre a foton fogalmát használjuk a fotoelektromos hatás magyarázatára, Einsteinhez hasonlóan.

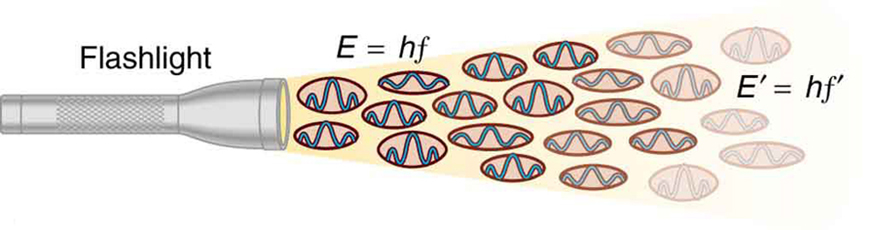
2. ábra. Az f frekvenciájú EM-hullám fotonokból, vagyis az EM-sugárzás egyes kvantumaiból áll. Az egyes fotonok energiája E = hf, ahol h a Planck-állandó, f pedig az EM-sugárzás frekvenciája. A nagyobb intenzitás több fotont jelent egységnyi területre vetítve. A zseblámpa nagyszámú, sok különböző frekvenciájú fotont bocsát ki, ezért mások energiája E′ = hf′, és így tovább.

A fotoelektromos hatás az alább tárgyalt tulajdonságokkal rendelkezik. Mindezek a tulajdonságok összhangban vannak azzal az elképzeléssel, hogy az EM-sugárzás egyes fotonjait az anyagban lévő egyes elektronok elnyelik, és az elektron elnyeri a foton energiáját. E tulajdonságok némelyike nincs összhangban azzal az elképzeléssel, hogy az EM-sugárzás egyszerű hullám. Az egyszerűség kedvéért nézzük meg, mi történik monokromatikus EM-sugárzással, amelyben minden fotonnak ugyanaz az energiája hf.

  1. Ha változtatjuk az anyagra eső EM-sugárzás frekvenciáját, a következőket találjuk: Egy adott anyag esetében az EM-sugárzásnak van egy f0 küszöbfrekvenciája, amely alatt az intenzitástól függetlenül nem lökődnek ki elektronok. Az egyes fotonok kölcsönhatásba lépnek az egyes elektronokkal. Ha tehát a foton energiája túl kicsi ahhoz, hogy egy elektront elszakítson, akkor nem fognak elektronok kilökődni. Ha az EM-sugárzás egyszerű hullám lenne, az intenzitás növelésével elegendő energiát lehetne elérni.
  2. Amint az EM-sugárzás egy anyagra esik, az elektronok késedelem nélkül kilökődnek. Amint egy elég nagy frekvenciájú egyedi foton elnyelődik egy egyedi elektron által, az elektron kilökődik. Ha az EM-sugárzás egyszerű hullám lenne, több perc kellene ahhoz, hogy elegendő energia rakódjon le a fémfelületre egy elektron kilökődéséhez.
  3. Az egységnyi idő alatt kilökődött elektronok száma arányos az EM-sugárzás intenzitásával és semmilyen más jellemzővel. A nagy intenzitású EM-sugárzás egységnyi területre jutó nagyszámú fotonból áll, és minden fotonnak ugyanaz a hf karakterisztikus energiája.
  4. Ha változtatjuk az EM-sugárzás intenzitását, és mérjük a kilökődött elektronok energiáját, a következőket találjuk: A kilökődött elektronok maximális mozgási energiája független az EM-sugárzás intenzitásától. Mivel egy anyagban nagyon sok elektron van, rendkívül valószínűtlen, hogy két foton egyszerre lépjen kölcsönhatásba ugyanazzal az elektronnal, és ezáltal növelje a neki adott energiát. Ehelyett (a fenti 3. pontban említettek szerint) a megnövekedett intenzitás több azonos energiájú elektron kilökődését eredményezi. Ha az EM-sugárzás egyszerű hullám lenne, nagyobb intenzitás több energiát adhatna, és nagyobb energiájú elektronok lökődnének ki.
  5. A kilökődött elektron kinetikus energiája egyenlő a foton energiájával mínusz az elektron kötési energiája az adott anyagban. Egy egyedi foton képes teljes energiáját átadni egy elektronnak. A foton energiája részben arra szolgál, hogy az elektron elszakadjon az anyagtól. A fennmaradó rész a kilökődött elektron mozgási energiájába megy át. Egyenlet formájában ez a következő: KEe = hf – BE, ahol KEe a kilökődött elektron maximális mozgási energiája, hf a foton energiája, BE pedig az elektron kötési energiája az adott anyaghoz. (A BE-t néha az anyag munkafüggvényének is nevezik.) Ez az egyenlet, amely Einsteinnek köszönhető 1905-ben, kvantitatív módon magyarázza a fotoelektromos hatás tulajdonságait. Az EM-sugárzás egy egyedi fotonja (máshogy nem jön létre) kölcsönhatásba lép egy egyedi elektronnal, elegendő energiát, BE-t szolgáltatva ahhoz, hogy az elektron elszakadjon, a maradék pedig mozgási energiává válik. A kötési energia BE = hf0, ahol f0 az adott anyag küszöbfrekvenciája. A 3. ábra a KEe maximumának grafikonját mutatja egy adott anyagra eső EM-sugárzás frekvenciájának függvényében.

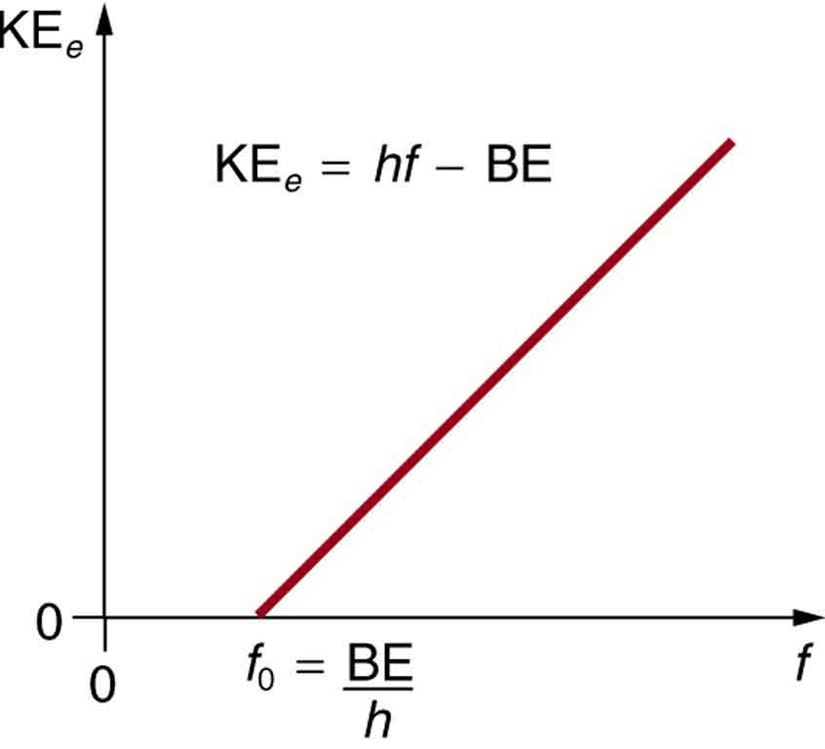
3. ábra. Fényelektromos hatás. A kidobott elektron kinetikus energiájának, KEe-nek a grafikonja egy adott anyagra eső EM-sugárzás frekvenciájának függvényében. Van egy küszöbfrekvencia, amely alatt nem lökődnek ki elektronok, mert az egyes elektronokkal kölcsönhatásba lépő egyes fotonok energiája nem elegendő az elektronok széttöréséhez. A küszöbenergia felett a KEe lineárisan nő az f értékkel, összhangban a KEe = hf – BE összefüggéssel. Ennek az egyenesnek a meredeksége h – az adatok felhasználhatók a Planck-állandó kísérleti meghatározására. Einstein adta az első sikeres magyarázatot ezekre az adatokra, amikor felvetette a fotonok – az EM-sugárzás kvantumai – gondolatát.

Einstein gondolata, hogy az EM-sugárzás kvantált, döntő jelentőségű volt a kvantummechanika kezdeteihez. Ez egy sokkal általánosabb fogalom, mint azt a fotoelektromos effektus magyarázata sugallná. Minden EM-sugárzás fotonok formájában is modellezhető, és az EM-sugárzás jellemzői teljes mértékben összhangban vannak ezzel a ténnyel. (Amint a következő részben látni fogjuk, az EM-sugárzás számos aspektusa, például az ultraibolya (UV) sugárzás veszélyei, csak a fotonok tulajdonságaival magyarázhatók). A modern relativitáselméletről híresebb Einstein 1905-ben, ugyanabban az évben, amikor a speciális relativitáselméletről szóló első tanulmányát publikálta, elültette a kvantummechanika fontos magját. A fotoelektromos hatás magyarázata volt az alapja az 1921-ben neki ítélt Nobel-díjnak. Bár az elméleti fizikához való egyéb hozzájárulásait is kiemelték ebben a díjban, a speciális és az általános relativitáselméletet nem ismerték el teljes mértékben annak ellenére, hogy 1921-re már részben kísérletekkel igazolták. Bár hősként tisztelték, ez a nagyszerű ember soha nem kapott Nobel-díjat leghíresebb munkájáért, a relativitáselméletért.

Példa 1. A fotonenergia és a fotoelektromos hatás kiszámítása: Egy lila fény

1. Mekkora a 420 nm-es ibolyántúli fény fotonjának energiája joule-ban és elektronvoltban kifejezve?

2. Mekkora a 420 nm-es ibolyántúli fény által a kalciumból kilökődő elektronok maximális mozgási energiája, ha az elektronok kötési energiája (vagy munkafüggvénye) a kalcium fém esetében 2,71 eV?

Stratégia

Az 1. rész megoldásához vegyük figyelembe, hogy a foton energiáját E = hf adja meg. A 2. részhez, miután kiszámítottuk a foton energiáját, a KEe = hf – BE egyenes alkalmazásával megtalálhatjuk a kilökődött elektron maximális mozgási energiáját, mivel a BE adott.

Az 1. rész megoldása

A foton energiáját az E = hf adja meg.

Mivel nem a frekvenciát, hanem a hullámhosszt kapjuk meg, a frekvenciára az ismert c = fλ összefüggést oldjuk meg, így f=\frac{c}{\lambda}\\\ kapjuk.

A két egyenlet kombinálásával az E=\frac{hc}{\lambda}\\\ hasznos összefüggést kapjuk.

Az ismert értékek behelyettesítésével megkapjuk

\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4.74\times10^{-19}\text{ J}\\

Átváltva eV-ra, a foton energiája

\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}{1.6\times10^{-19}\text{ J}}=2.96\text{ eV}\\

A 2. rész megoldása

A kilökött elektron kinetikus energiájának meghatározása most a KEe = hf – BE egyenlet egyszerű alkalmazása. A foton energiáját és a kötési energiát behelyettesítve a KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV eredményt kapjuk.

Diszkusszió

A 420 nm-es ibolyántúli fény fotonjának energiája a joule parányi töredéke, így nem csoda, hogy egyetlen fotont nehéz lenne közvetlenül érzékelnünk – az emberek inkább a joule nagyságrendű energiákra vannak beállítva. De ha az energiát elektronvoltban nézzük, láthatjuk, hogy ennek a fotonnak elég energiája van ahhoz, hogy hatással legyen az atomokra és molekulákra. Egy DNS-molekula például körülbelül 1 eV energiával megtörhető, és a tipikus atomi és molekuláris energiák eV nagyságrendűek, így az UV-foton ebben a példában biológiai hatásokkal járhat. A kilökött elektron (fotoelektron) energiája meglehetősen alacsony, és nem jutna messzire, kivéve vákuumban. Az elektront egy mindössze 0,26 eV-os lassító potenciál állítaná meg. Valójában, ha a foton hullámhossza hosszabb lenne, és energiája kisebb, mint 2,71 eV, akkor a képlet negatív mozgási energiát adna, ami lehetetlen. Ez egyszerűen azt jelenti, hogy a 420 nm-es fotonok 2,96 eV energiájukkal nem sokkal a frekvenciaküszöb felett vannak. Magad is megmutathatod, hogy a küszöb hullámhossza 459 nm (kék fény). Ez azt jelenti, hogy ha egy fénymérőben kalciumfémet használunk, a mérő érzéketlen lesz a kék fénynél hosszabb hullámhosszakra. Egy ilyen fénymérő például teljesen érzéketlen lenne a vörös fényre.

PhET Explorations:

Kattints a szimuláció letöltéséhez. Java segítségével futtatható.

Közlemény

  • A fotoelektromos hatás az a folyamat, amelynek során az EM-sugárzás elektronokat lök ki egy anyagból.
  • Einstein a fotonokat az EM-sugárzás E = hf energiájú kvantumainak javasolta, ahol f a sugárzás frekvenciája.
  • Minden EM-sugárzás fotonokból áll. Ahogy Einstein kifejtette, a fotoelektromos hatás minden jellemzője az egyes fotonok és az egyes elektronok kölcsönhatásának köszönhető.
  • A kilökődött elektronok (fotoelektronok) maximális mozgási energiája KEe a KEe = hf – BE, ahol hf a foton energiája, BE pedig az elektron kötési energiája (vagy munkafüggvénye) az adott anyaghoz.

Fogalmi kérdések

  1. A látható fény az egyetlen EM-sugárzástípus, amely a fotoelektromos effektust okozhatja?
  2. A fotoelektromos effektus mely aspektusai nem magyarázhatók fotonok nélkül? Melyek magyarázhatók fotonok nélkül? Az utóbbiak ellentmondanak-e a fotonok létezésének?
  3. A fotoelektromos hatás az EM-sugárzás hullámjellegének vagy az EM-sugárzás részecskejellegének közvetlen következménye? Magyarázza meg röviden.
  4. A szigetelők (nemfémek) BE értéke magasabb, mint a fémeké, és a fotonok számára nehezebb az elektronok kilökése a szigetelőkből. Beszélje meg, hogy ez hogyan függ össze a fémekben lévő szabad töltésekkel, amelyek jó vezetővé teszik őket.
  5. Ha felveszünk és megrázunk egy fémdarabot, amelyben az elektronok szabadon áramként mozognak, nem esnek ki elektronok. Mégis, ha felmelegíted a fémet, az elektronok kiforrnak belőle. Magyarázza meg mindkét tényt a tárgy rázásával járó energia mennyiségével és eloszlásával kapcsolatban, összehasonlítva a tárgy melegítésével.

Problémák & Gyakorlatok

  1. Melyik a leghosszabb hullámhosszú EM-sugárzás, amely képes egy fotoelektron kilökésére az ezüstből, ha a kötési energia 4,73 eV? Ez a látható tartományban van?
  2. Keresd meg azt a legnagyobb hullámhosszúságú fotonsugárzást, amely káliumból elektront tud kilökni, ha a kötési energia 2,24 eV. Ez látható EM-sugárzás?
  3. Mi a magnézium elektronjainak kötési energiája eV-ban, ha a leghosszabb hullámhosszúságú foton, amely képes elektronokat kilökni, 337 nm?
  4. Kalkulálja ki az alumínium elektronjainak kötési energiáját eV-ban, ha a leghosszabb hullámhosszúságú foton, amely képes elektronokat kilökni, 304 nm.
  5. Melyik a 450 nm-es EM-sugárzással nátriumfémből kilökődő elektronok maximális kinetikus energiája eV-ban, ha a kötési energia 2,28 eV?
  6. A 120 nm hullámhosszúságú UV-sugárzás esik az aranyfémre, amelyhez az elektronok 4,82 eV kötéssel kapcsolódnak. Mekkora a kilökődött fotoelektronok maximális mozgási energiája?
  7. A 400 nm hullámhosszúságú ibolyántúli fény 0,860 eV maximális mozgási energiájú elektronokat lök ki a nátriumfémből. Mekkora az elektronok kötési energiája a nátriumfémhez?
  8. A 300 nm hullámhosszú UV-sugárzás az uránfémre esik, és 0,500 eV-os elektronokat lök ki. Mekkora az uránfém elektronjainak kötési energiája?
  9. a) Mekkora annak az EM-sugárzásnak a hullámhossza, amely 2,00 eV-os elektronokat lök ki a kalciumfémből, ha a kötési energia 2,71 eV? (b) Milyen típusú EM-sugárzásról van szó?
  10. Keresd meg a káliumból 0,100-eV elektronokat kilökő fotonok hullámhosszát, ha a kötési energia 2,24 eV. Ezek a fotonok láthatóak?
  11. Mekkora a maximális sebessége a 80 nm-es fotonok által egy anyagból kilökött elektronoknak, ha azok 4,73 eV kötési energiával kötődnek az anyaghoz?
  12. A 2,71 eV kötési energiájú anyagból 420 nm-es fotonok által kilökött fotonok. A kilökődés után mennyi idő alatt jutnak el ezek az elektronok 2,50 cm-t egy detektáló eszközig?
  13. Egy 2,00 mW teljesítményű, 400 nm hullámhosszúságú lézert vetítünk kalciumfémre. (a) Hány elektron lövell ki másodpercenként? (b) Mekkora teljesítményt visznek el az elektronok, tekintve, hogy a kötési energia 2,71 eV?
  14. (a) Számítsuk ki, hány fotoelektron lökődik ki másodpercenként egy 1,00 mm 2 -es nátrium-fém területről az 1,30 kW/m2 intenzitású 500 nm-es EM-sugárzás (a napfény intenzitása a Föld légköre felett) hatására. (b) Tekintettel arra, hogy a kötési energia 2,28 eV, mekkora teljesítményt visznek el az elektronok? (c) Az elektronok kevesebb energiát visznek el, mint amennyit a fotonok hoztak be. Hová vándorol a többi energia? Hogyan nyerhető vissza?
  15. Értelmezhetetlen eredmények. 700 nm hullámhosszúságú vörös fényt vetítünk magnéziumfémre, amelyhez 3,68 eV elektronok kötődnek. (a) Számítsuk ki KEe = hf – BE segítségével a kilökődött elektronok kinetikus energiáját. (b) Mi az ésszerűtlen ebben az eredményben? (c) Milyen feltételezések ésszerűtlenek vagy következetlenek?
  16. Indokolatlan eredmények. (a) Mekkora az elektronok kötési energiája egy olyan anyaghoz, amelyből 4,00 eV-os elektronokat lök ki a 400 nm-es EM-sugárzás? (b) Mi az ésszerűtlen ebben az eredményben? (c) Milyen feltételezések ésszerűtlenek vagy ellentmondásosak?

Glosszárium

fotoelektromos hatás: az a jelenség, amelynek során egyes anyagok elektronokat löknek ki, ha fényt bocsátanak rájuk

foton: az elektromágneses sugárzás kvantuma vagy részecskéje

fotonenergia: E = hf

kötési energia: más néven munkafüggvény; az az energiamennyiség, amely ahhoz szükséges, hogy egy elektron kilökődjön egy anyagból

Válogatott feladatmegoldások & Gyakorlatok

1. 263 nm

3. 3,69 eV

5. 0,483 eV

7. 2,25 eV

9. (a) 264 nm; (b) ultraibolya

11. 1,95 × 106 m/s

13. (a) 4,02 × 1015 s; (b) 0,256 mW

15. (a) -1,90 eV; (b) Negatív mozgási energia; (c) Hogy az elektronok szabaddá válnának

.

Vélemény, hozzászólás?

Az e-mail-címet nem tesszük közzé.