A víz fázisdiagramja
A 11.23. ábra “A víz fázisdiagramjának két változata” a víz fázisdiagramját mutatja, és szemlélteti, hogy a víz hármaspontja 0,01 °C-on és 0,00604 atm (4,59 mmHg) hőmérsékleten van. A hármaspont (273,16 K) sokkal jobban reprodukálható, mint a jég olvadáspontja, amely az oldott levegő mennyiségétől és a légköri nyomástól függ, és az abszolút (Kelvin) hőmérsékleti skála meghatározására szolgál. A hármaspont jelenti azt a legalacsonyabb nyomást is, amelyen egy folyékony fázis egyensúlyban létezhet a szilárd anyaggal vagy gőzzel. A 0,00604 atm-nál kisebb nyomáson tehát a jég a hőmérséklet emelkedésével nem olvad folyadékká; a szilárd anyag közvetlenül vízgőzzé szublimál. A víz alacsony hőmérsékleten és nyomáson történő szublimációja felhasználható élelmiszerek és italok “fagyasztva szárítására”. Az ételt vagy italt először fagypont alatti hőmérsékletre hűtik, majd olyan tartályba helyezik, amelyben a nyomást 0,00604 atm alatt tartják. Ezután a hőmérséklet növelésével a víz szublimál, és megmarad a dehidratált élelmiszer (mint például a hátizsákos utazók vagy űrhajósok által használt) vagy a porított ital (mint a fagyasztva szárított kávé esetében).
A 11.23. ábra “A víz fázisdiagramjának két változata” b) részében ábrázolt víz fázisdiagramja a jég és a víz közötti határt mutatja kiterjesztett méretarányban. A jég olvadási görbéje felfelé és enyhén balra lejt, nem pedig felfelé és jobbra, mint a 11.22. ábrán “Egy olyan anyag tipikus fázisdiagramja, amely három fázist – szilárd, folyékony és gáz – és egy szuperkritikus régiót mutat”; vagyis a jég olvadáspontja a nyomás növekedésével csökken; 100 MPa (987 atm) nyomáson a jég -9°C-on olvad meg. A víz azért viselkedik így, mert egyike azon kevés ismert anyagoknak, amelyeknél a kristályos szilárd anyag kisebb sűrűségű, mint a folyadék (a többi közé tartozik az antimon és a bizmut). A vízzel 0°C-on és 1 atm-on egyensúlyban lévő jég nyomásának növelése a molekulák egy részét közelebb tolja egymáshoz, így a minta térfogata csökken. A térfogatcsökkenés (és az ennek megfelelő sűrűségnövekedés) kisebb egy szilárd vagy folyékony anyag esetében, mint egy gáz esetében, de elegendő ahhoz, hogy a jég egy része megolvadjon.
11.23. ábra A víz fázisdiagramjának két változata
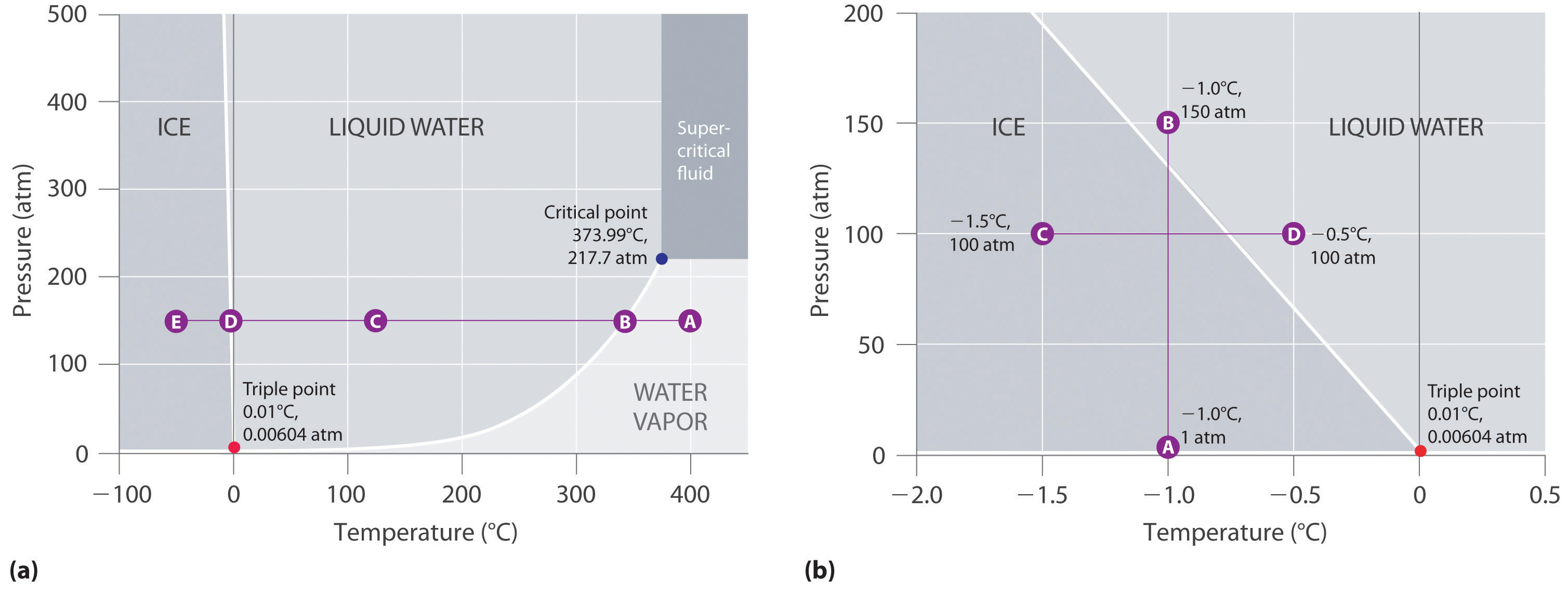
(a) Ezen a lineáris hőmérséklet- és nyomástengelyű ábrán a jég és a folyékony víz közötti határ szinte függőleges. (b) Ez a kiterjesztett skálával készült grafikon az olvadáspont csökkenését szemlélteti a nyomás növekedésével. (A betűk a 10. példában tárgyalt pontokra utalnak.)
A 11.23. ábra “A víz fázisdiagramjának két változata” (b) részében az A pont P = 1 atm és T = -1,0°C mellett található, a fázisdiagram szilárd (jég) tartományában. Ahogy a nyomás 150 atm-ra nő, miközben a hőmérséklet változatlan marad, az A pontból kiinduló vonal a jég/víz határon át a B pontba vezet, amely a folyékony víz tartományban helyezkedik el. Következésképpen 150 atm nyomás alkalmazása -1,0°C-os jeget olvaszt meg. Már jeleztük, hogy a víz olvadáspontjának nyomásfüggése alapvető fontosságú. Ha a szilárd/folyékony határ a víz fázisdiagramján balra helyett felfelé és jobbra dőlne, a jég sűrűbb lenne, mint a víz, a jégkockák elsüllyednének, a vízvezetékek nem törnének szét, amikor megfagynak, és a fagyálló folyadékra nem lenne szükség az autómotorokban.
A közelmúltig sok tankönyv úgy írta le a korcsolyázást, mint ami azért lehetséges, mert a korcsolyázó pengéje által generált nyomás elég nagy ahhoz, hogy a pengéje alatti jeget megolvassza, és ezáltal egy folyékony vízből álló kenőréteget hoz létre, amely lehetővé teszi a pengének a jégen való csúszást. Bár ez a magyarázat intuitívan kielégítő, helytelen, amint azt egy egyszerű számítással megmutathatjuk. Emlékezzünk vissza a 10. fejezet “Gázok” című fejezetéből, hogy a nyomás (P) az egységnyi területre (A) kifejtett erő (F):
11.4. egyenlet
P = F A
A korcsolyázó által a jégre kifejtett nyomás kiszámításához csak a kifejtett erőt és a korcsolyapenge területét kell kiszámítanunk. Ha egy 75,0 kg-os (165 lb) korcsolyázót feltételezünk, akkor a korcsolyázó által a jégre a gravitáció miatt kifejtett erő
egyenlet 11.5
F = mg
ahol m a tömeg, g pedig a Föld gravitációja miatti gyorsulás (9,81 m/s2). Így az erő
egyenlet 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Ha feltételezzük, hogy a korcsolyapengék 2.0 mm szélesek és 25 cm hosszúak, akkor az egyes pengék aljának területe
egyenlet 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Ha a korcsolyázó egy lábon siklik, akkor a jégre kifejtett nyomás
egyenlet 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
A nyomás jóval kisebb, mint a jég olvadáspontjának akár 1°C-kal való csökkentéséhez szükséges nyomás, és a tapasztalatok szerint akkor is lehet korcsolyázni, ha a hőmérséklet jóval fagypont alatt van. Így a jég nyomás okozta olvadása nem magyarázhatja a korcsolyázók (és a jégkorongok) siklását lehetővé tevő alacsony súrlódást. A legújabb kutatások szerint a jég felszíne, ahol a vízmolekulák rendezett sorozata találkozik a levegővel, egy vagy több, szinte folyékony vízből álló rétegből áll. Úgy tűnik, hogy ezek a rétegek a súrlódás okozta olvadással együtt, amikor a korcsolyázó előre nyomul, magyarázatot adnak mind arra, hogy a korcsolyázó milyen könnyen siklik, mind arra, hogy a korcsolyázás -7°C alatt nehezebbé válik, amikor a kenőanyagként szolgáló felszíni vízrétegek száma csökken.
