Tudomány > Fizika > Fényelektromos hatás >Einstein fotoelektromos egyenlete
Ebben a cikkben, levezetjük Einstein fotoelektromos egyenletét és megvizsgáljuk annak használatát a fény fotoelektromos hatásának jellemzőinek ellenőrzésére.
A fény hullámtermészete:
Christian Huygen javasolta, hogy a fény hullám formájában terjed. Ennek az elméletnek azonban van egy komoly hátránya. Nem tudta megmagyarázni a fény terjedését vákuumban. Ezt a hátrányt Maxwell megszüntette, aki azt javasolta, hogy a fény elektromágneses hullám, és az elektromágneses hullámok terjedéséhez nincs szükség anyagi közegre. Ezzel megállapította a fény hullámtermészetét.
A hullámelmélet képes volt megmagyarázni a fény terjedésével kapcsolatos összes jelenséget. De nem tudta megmagyarázni az energiaeloszlást és az olyan modern jelenségeket, mint a fotoelektromos hatás, a Crompton-effektus stb.
A fény részecsketermészetét:
Max Planck bebizonyította, hogy a fény vagy az energia terjedése kvantumoknak nevezett energiacsomagok formájában történik. A fénykvantumot fotonnak nevezik, és ezzel megállapította a fény részecskenyészetét. A sugárzás részecske- vagy kvantumtermészetét felhasználva magyarázhatjuk a fotoelektromos hatás és a Crompton-effektus jelenségét.
Planck kvantumelmélete:
A kvantumelméletet Max Planck javasolta. Ezen elmélet szerint egy forrásból származó sugárzás nem folyamatosan, hanem energiacsomagokban vagy -kötegekben bocsátódik ki. Ezeket a csomagokat kvantumoknak vagy fotonoknak nevezzük. Ha a sugárzás ν frekvenciájú, minden egyes kvantumnak energiája van, ahol h a Planck-állandó.
A foton energiája tehát = E = hν
Az energia diszkontinuusan bocsátódik ki. Ez ellentétes a klasszikuselmélettel, amely az energia kibocsátását folyamatos folyamatnak feltételezi.
Elektromágneses sugárzások részecske jellege:
A sugárzás és az anyag kölcsönhatásában a sugárzás úgy viselkedik, mintha részecskékből állna. Ezeket a részecskéket fotonoknak nevezzük. Minden egyes fotonnak energiája van, amely a következők szerint adódik:
E = hν = hc/λ
Az adott frekvenciájú (hullámhosszú) fény minden fotonjához ugyanannyi energia tartozik. A fény intenzitásának növekedése növeli az adott területen másodpercenként áthaladó fotonok számát, de az egyes fotonok energiája nem változik. A fotonok elektromosan semlegesek, és az elektromos vagy mágneses mezők nem befolyásolják őket. A fotonok egyenes vonalban haladnak a fény “c” sebességével, de bizonyos körülmények között diffrakciót mutatnak.
Az egyes fotonok impulzusmomentuma
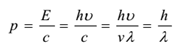
A fotonok hullámhossza a közeggel változik, ezért a különböző közegekben különböző sebességgel rendelkeznek. A foton nyugalmi tömege nulla. A kinetikus tömege a következő:
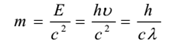
A foton részecskék ütközésénél (például foton-elektron ütközésnél) a teljes energia és az impulzus megőrződik. A fotonok száma azonban nem feltétlenül marad meg az ütközésben. A foton elnyelődhet, vagy új foton keletkezhet.
Einstein fotoelektromos egyenlete:
A Planck-féle kvantumelmélet alapján Einstein levezetett egy egyenletet a fotoelektromos hatásra, amelyet Einstein fotoelektromos egyenlete néven ismerünk. Einstein feltételezte, hogy
- A fény fotonokból vagy energiakvantumokból áll, az egyes fotonokban lévő energia hν. Ahol h a Planck-állandó és ν a fény frekvenciája
- Minden beeső foton ütközik egy atomban lévő elektronnal, és minden energiáját átadja az elektronnak.
- Ez energia egy részét az elektron arra használja fel, hogy kilépjen a fém felületéből, a fennmaradó rész pedig az a mozgási energia, amellyel az elektron kilép.
- Azt a minimális energiát, amely egy elektron számára szükséges ahhoz, hogy kilépjen a fém felületéből, a fém fotoelektromos munkafüggvényének (∅o) nevezzük.
- A fennmaradó energia (hν – ∅o) az elektron maximális mozgási energiája, amellyel a fotoelektron kilökődik.
Egy elektron maximális mozgási energiája = foton energiája – munkafüggvény
Legyen “m” az elektron tömege és vmax a fotoelektron maximális sebessége, amellyel kilökődik.

Ezt az egyenletet Einstein fotoelektromos egyenletének nevezik
Fotoelektromos munkafüggvény:
A fotoelektromos effektusban a fényérzékeny anyag atomjának leglazább kötésű elektronja távolodik el. Az adott felületről egy elektron kiszabadításához szükséges minimális energiát a felület anyagának fotoelektromos munkafüggvényének (∅o) nevezzük. A munkafüggvény a fémfelület jellemző tulajdonsága.
Matematikailag a munkafüggvény a
∅o = h νo
Hol νo =küszöbfrekvencia és h =Planck-állandó.
A küszöbfrekvencia létezésének magyarázata az Einstein-féle fotoelektromos egyenlet alapján:
Egy adott fémfelület esetében fotoelektronok csak akkor emittálódnak, ha a beeső fény frekvenciája nagyobb vagy egyenlő egy bizonyos minimális frekvenciánál (no)-nak nevezett küszöbfrekvenciánál. A küszöbfrekvencia különböző anyagokra eltérő,
Az Einstein-féle fotoelektromos egyenlet

amelyben νo = küszöbfrekvenciaés h = Planck-állandó és
ν = a beeső sugárzás frekvenciája
A mozgási energia mindig nem negatív mennyiség i.azaz lehet pozitív vagy nulla, tehát

Ami azt jelzi, hogy a fotoelektromos hatáshoz a beeső sugárzás vagy beeső foton frekvenciájának egyenlőnek vagy nagyobbnak kell lennie a küszöbfrekvenciánál. A különböző atomokban a valószínű fotoelektronokra ható vonzóerő eltérő. Ezért a küszöbfrekvencia a különböző anyagok esetében eltérő.
Az intenzitás hatásának magyarázata azEinstein-féle fotoelektromos egyenlet alapján:
Ha a beeső fény frekvenciája kisebb, mint a küszöbfrekvencia,a fotoelektronok nem emittálódnak, bármilyen nagy is legyen a beeső fény intenzitása.
A másodpercenként kibocsátott fotoelektronok száma egyenesen arányos a beeső fény intenzitásával. Így a fotoelektromos áram egyenesen arányos a beeső fény intenzitásával. Ha a fény intenzitása nagyobb, akkor a felületre beeső fotonok száma is több. A megnövekedett fotoelektronszám miatt a fotoemisszió sebessége nő, így a fotoelektromos áram erőssége is nő. Így megállapíthatjuk, hogy a fotoelektromos hatás (áram) egyenesen arányos a beeső sugárzás intenzitásával.
A lehetséges maximális kinetikus energia magyarázata az Einstein-féle fotoelektromos egyenlet alapján:
Az Einstein-féle fotoelektromos egyenlet

Ahol νo = küszöbfrekvenciaés h = Planck-állandó és
ν = a beeső sugárzás frekvenciája
Az egyenlet nem tartalmazza az intenzitás kifejezését, így azt mondhatjuk, hogy a fotoelektron maximális mozgási energiája független a beeső sugárzás intenzitásától, de függ a beeső sugárzás frekvenciájától. Ez az egyenlet azt mutatja, hogy az elektron maximális mozgási energiája a beeső sugárzás frekvenciájától függ. És ha a beeső sugárzás frekvenciája megnő, akkor a fotoelektron kinetikus energiája is megnő.
A fotoelektromos hatás pillanatnyiságának magyarázata az Einstein-féle fotoelektromos egyenlet alapján:
A fotoelektromos hatás pillanatnyi folyamat. Nincs időeltolódás a fény beesése és a fotoelektronok kibocsátása között, más szóval a felület azonnal elkezd fotoelektronokat kibocsátani, amint fény esik rá. A fotoelektronok emissziója is abbamarad abban a pillanatban, amikor a beeső fény megszűnik.
Amikor a fénykibocsátó felületre abban a pillanatban sugárzás esik, a foton teljes energiája egyetlen elektronra száll át. Így az elektron időbeli késleltetés nélkül emittálódik, és a fotoelektromos hatás pillanatnyi folyamat.
Előző téma:
Következő téma: Numerikus feladatok a fotoelektromos effektussal kapcsolatban
Következő téma: A fotoelektromos hatás számítási feladatai: Fényelektromos egyenlet numerikus feladatai
Tudomány > Fizika > Fényelektromos hatás >Einstein fényelektromos egyenlete
.
