A csoport 
olyan elemek véges vagy végtelen halmaza egy bináris művelettel (az úgynevezett csoportművelettel) együtt, amelyek együttesen kielégítik a négy alapvető tulajdonságot: a zártság, az asszociativitás, az azonossági tulajdonság és az inverz tulajdonság. A műveletet, amellyel kapcsolatban egy csoportot definiálnak, gyakran “csoportműveletnek” nevezik, és egy halmazról azt mondják, hogy “e művelet alatt” csoport. A 
, 
, 
, … elemek 
és 
közötti bináris művelettel jelölve 
csoportot alkotnak, ha
1. Zárás: Ha 
és 
a 
két eleme, akkor a 
szorzata is a 
-ben van.
2. Asszociativitás: A definiált szorzás asszociatív, azaz minden 
, 
esetén .
3. Azonosság: Van egy olyan 
azonossági elem (más néven 1, 
vagy 
), hogy 
minden 
elemre .
4. Inverz: Minden elemnek kell lennie egy inverzének (más néven reciprokának). Ezért a 
minden 
eleméhez a halmaz tartalmaz egy olyan 
elemet, hogy 
.
A csoport olyan monoid, amelynek minden eleme invertálható.
A csoportnak legalább egy elemet kell tartalmaznia, az egyetlen (izomorfizmusig) egyelemű csoportot triviális csoportnak nevezzük.
A csoportok tanulmányozását csoportelméletnek nevezzük. Ha véges számú eleme van, a csoportot véges csoportnak nevezzük, az elemek számát pedig a csoport csoportsorrendjének. Egy csoportnak azt a részhalmazát, amely a csoportművelet és az inverz művelet alatt zárt, alcsoportnak nevezzük. Az alcsoportok is csoportok, és sok gyakran előforduló csoport valójában valamilyen általánosabb nagyobb csoport speciális alcsoportja.
A véges csoport alapvető példája a 
szimmetrikus csoport, amely 
objektumok permutációinak (vagy “permutáció alatti”) csoportja. A legegyszerűbb végtelen csoport az egész számok halmaza a szokásos összeadás alatt. Folytonos csoportoknak tekinthetjük a valós számokat vagy a 
invertálható mátrixok halmazát. Ez utóbbi kettő a Lie-csoportok példája.
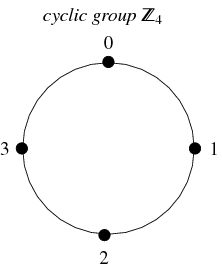
A csoport egyik nagyon gyakori típusa a ciklikus csoportok. Ez a csoport izomorf az egész számok csoportjával (modulo 
), jelölése 
, 
vagy 
, és minden 
egész számra definiált. Összeadás alatt zárt, asszociatív, és egyedi inverzekkel rendelkezik. Elemeit a 0-tól 
-ig terjedő számok jelölik, az azonossági elemet a 0 jelöli, 
inverzét pedig 
.
A két csoport közötti leképezést, amely megőrzi az azonosságot és a csoportműveletet, homomorfizmusnak nevezzük. Ha egy homomorfizmusnak van inverze, amely szintén homomorfizmus, akkor izomorfizmusnak nevezzük, és a két csoportot izomorfnak nevezzük. Két egymáshoz izomorf csoportot absztrakt csoportként tekintve “azonosnak” tekintünk. Például egy négyzet forgatásainak alább ábrázolt csoportja a ciklikus csoport 
.
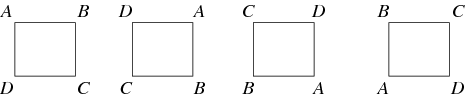
Általában csoporthatásról akkor beszélünk, ha egy csoport úgy hat egy halmazra, hogy annak elemeit permutálja, hogy a csoportról a halmaz permutációs csoportjára való leképezés homomorfizmus. Például egy négyzet forgatásai a négyzet sarkainak permutációinak alcsoportja. Bármely csoport 
egyik fontos csoportakciója a konjugációval önmagán végzett akciója. Ez csak néhány a lehetséges csoport-automorfizmusok közül. A csoporthatás másik fontos fajtája a csoportreprezentáció, ahol a csoport invertálható lineáris leképezésekkel hat egy vektortérre. Ha a vektortér mezője a komplex számok, akkor a reprezentációt néha CG-modulnak nevezik.
A csoporthatások, és különösen a reprezentációk nagyon fontosak az alkalmazásokban, nemcsak a csoportelméletben, hanem a fizikában és a kémiában is. Mivel egy csoportot absztrakt matematikai objektumként lehet elképzelni, ugyanaz a csoport különböző kontextusokban is előfordulhat. Ezért hasznos, ha a csoport reprezentációjára úgy gondolunk, mint a csoport egy bizonyos megtestesülésére, amelynek más reprezentációi is lehetnek. Egy csoport irreducibilis reprezentációja olyan reprezentáció, amelyre nem létezik olyan unitárius transzformáció, amely a reprezentációs mátrixot blokkdiagonális formába alakítja. Az irreducibilis reprezentációk számos figyelemre méltó tulajdonsággal rendelkeznek, amelyeket a csoport ortogonalitási tételében formalizáltak.