Adatszerkezetek 101: Táblák – vizuális bevezetés kezdőknek

Ismerje meg a mindennap használt adatszerkezeteket.

👋 Üdvözöljük! Kezdjük néhány létfontosságú összefüggéssel. Hadd kérdezzem meg a következőt!
✅ Hallgatsz-e zenét az okostelefonodon?
✅ Vezetsz-e névjegyzéket a telefonodon?
✅ Láttál-e már valaha ranglistát egy versenyen?

Ha a válaszod “igen” bármelyik kérdésre, akkor szinte biztos, hogy használtál már tömböket, és nem is tudtál róla! 😃 A tömbök nagyon hatékony adatszerkezetek, amelyek elemek listáit tárolják. Végtelen számú alkalmazásuk van. Nagyon fontosak a számítástechnika világában.

Ebben a cikkben megismerheted a tömbök előnyeit és hátrányait, felépítésüket, műveleteiket és felhasználási területeiket.

Kezdjük! 👍

🔎 Mélymerülés a tömbök alapvető szerkezetébe

A működésük megértéséhez nagyon hasznos, ha a számítógép memóriáját az alábbi képhez hasonló rácsként képzeled el. Minden egyes információ a rácsot alkotó kis elemek (négyzetek) egyikében tárolódik.

A tömbök ezt a “rács” szerkezetet használják ki arra, hogy egymáshoz kapcsolódó információk listáit szomszédos memóriahelyeken tárolják, így garantálva az értékek megtalálásának rendkívüli hatékonyságát. 🔳🔳🔳🔳 🔳

A tömbökre így gondolhatunk:

Elemeik egymás mellett vannak a memóriában. Ha egynél többhöz kell hozzáférned, a folyamat rendkívül optimalizált, mert a számítógéped már tudja, hol található az adott érték.

Félelmetes, igaz? Ismerjük meg, hogyan működik mindez a színfalak mögött! 😃

📚 Osztályozás

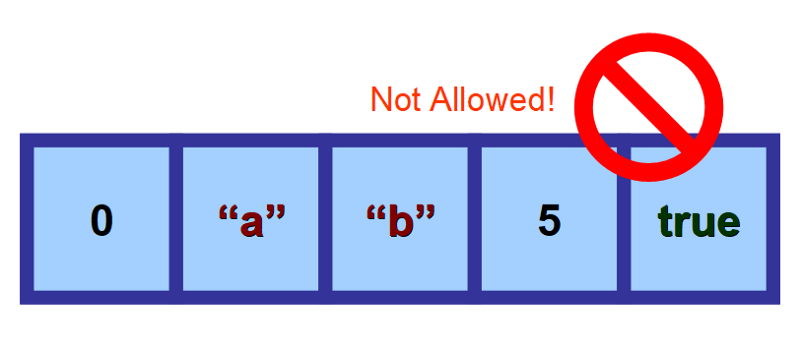
A tömböket a homogén adatszerkezetek közé soroljuk, mivel azonos típusú elemeket tárolnak.

Tárolhatnak számokat, karakterláncokat, boolék értékeket (igaz és hamis), karaktereket, objektumokat és így tovább. De ha egyszer meghatároztad, hogy milyen típusú értékeket fog tárolni a tömböd, akkor minden elemének ugyanahhoz a típushoz kell tartoznia. Nem “keverheted” a különböző típusú adatokat.

👀 Értékek olvasása – kezdődik a varázslat!

A tömbök elképesztő ereje az értékekhez való hozzáférés hatékonyságából ered. Ezt a rácsszerű felépítésnek köszönhetően érjük el. Nézzük meg ezt részletesebben.🔍

Mikor létrehozol egy tömböt, akkor:
– Hozzárendeled egy változóhoz. 👈
– Meghatározod, hogy milyen típusú elemeket fog tárolni. 🎈
– Meghatározod a méretét (az elemek maximális számát). 📚

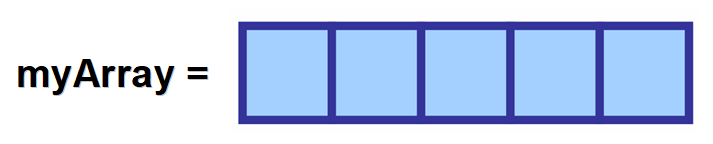
💡 Megjegyzés: A név, amelyet ehhez a változóhoz rendelsz, nagyon fontos, mert később a kódodban ezt fogod használni az értékek elérésére és a tömb módosítására.

De hogyan tudod megmondani a számítógépnek, hogy melyik konkrét értéket szeretnéd elérni? Ez az, ahol az indexek létfontosságú szerepet kapnak!

1️⃣ Indexek

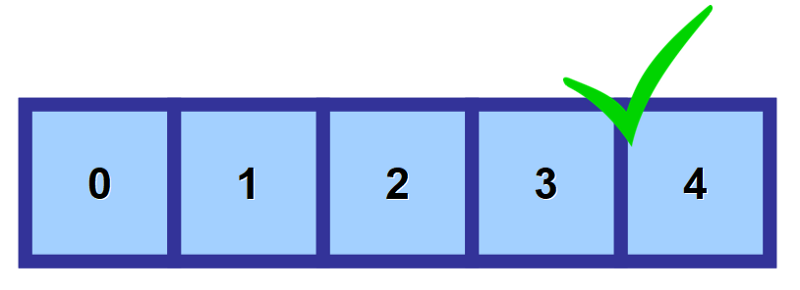
Egy tömbben lévő érték eléréséhez úgynevezett “indexet” (“indexek” többes számban) használsz. Ez egy szám, amely arra a helyre utal, ahol az értéket tárolják.

Amint az alábbi ábrán látható, a tömb első elemére a 0. index segítségével hivatkozunk. Ahogy haladunk tovább jobbra, az index minden egyes memóriahelyen eggyel nő.

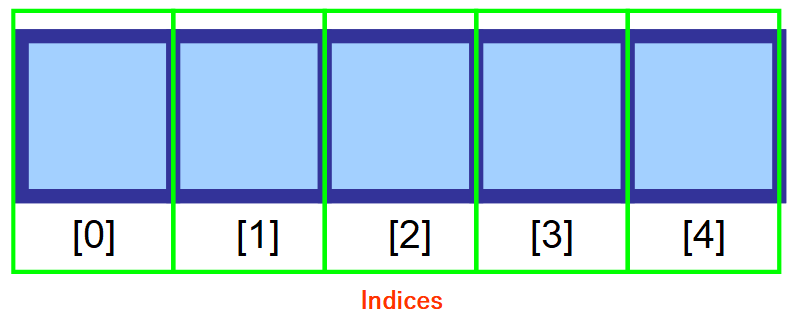
💡 Megjegyzés: Tudom, hogy elsőre furcsának tűnik, hogy 1 helyett 0-ról kezdjük a számolást, de ezt hívják nullás alapú számozásnak. Ez nagyon gyakori az informatikában.

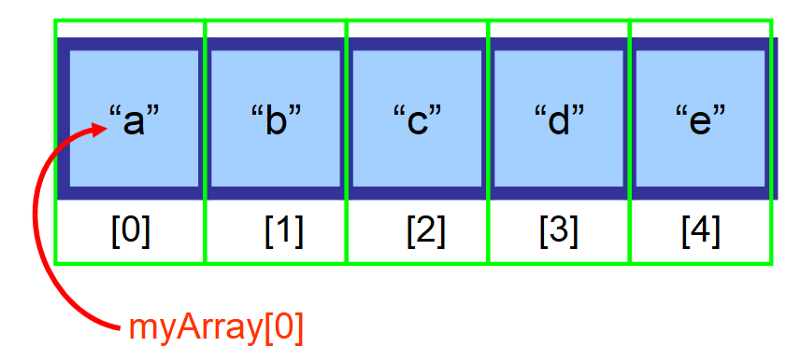
Az általános szintaxis egy elem eléréséhez a következő: <ArrayVariable>

Például:
Ha a tömböt a myArray változóban tároljuk, és az első elemhez (a 0 indexen) szeretnénk hozzáférni, akkor a myArray

2️⃣ Memória

Most, hogy már tudjuk, hogyan érhetjük el az értékeket, nézzük meg, hogyan tárolódnak a tömbök a számítógép memóriájában. Amikor meghatározod a tömb méretét, attól a pillanattól kezdve a memóriában lévő összes helyet “lefoglalják” a jövőben esetleg beilleszteni kívánt értékek számára.

💡 Megjegyzés: Ha nem töltöd fel a tömböt értékekkel, akkor ez a hely addig marad lefoglalva és üresen, amíg ezt meg nem teszed.

Példa:
Tegyük fel, hogy definiálsz egy 5 méretű tömböt, de csak egy értéket illesztesz be. Az összes fennmaradó hely üres és “lefoglalt” lesz a memóriában, várva a jövőbeli hozzárendelésekre.

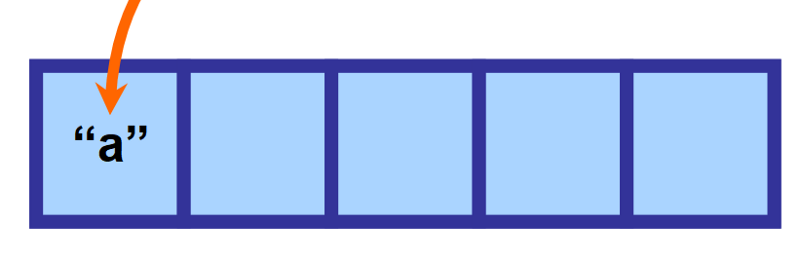
Ez azért kulcsfontosságú, mert a tömbök rendkívül hatékonyak az értékek elérésében, mivel minden elemet egybefüggő helyeken tárolnak a memóriában. Így a számítógép pontosan tudja, hogy hol keresse a kért információt.

De… ennek van egy hátulütője 😞 mert ez nem memóriahatékony. Olyan jövőbeli műveletekre tartogatod a memóriát, amelyek esetleg nem következnek be. Ezért a tömböket olyan helyzetekben ajánljuk, amikor előre tudod, hogy hány elemet fogsz tárolni.

🔧 Műveletek – a színfalak mögött!

Most, hogy már tudod, milyenek a tömbök, amikor használják őket, és hogyan tárolják az elemeket, belemerülünk a műveleteikbe, mint a beszúrás és az eltávolítás.

1️⃣ Beszúrás – Üdvözöljük!

Tegyük fel, hogy van egy 6-os méretű tömbünk, és még van egy üres hely. A tömb elejére (index 0) szeretnénk beszúrni egy “e” elemet, de ezt a helyet már elfoglalta az “a” elem. Mit tegyünk?

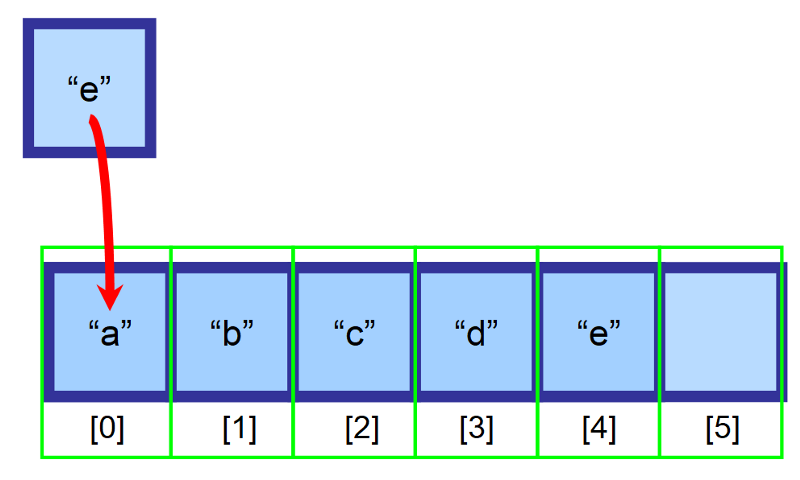
A tömbökbe való beszúráshoz a beszúrás helyétől jobbra található összes elemet áthelyezzük egy indexszel jobbra. Az “a” elem mostantól az 1-es indexen lesz, a “b” elem a 2-es indexen, és így tovább…

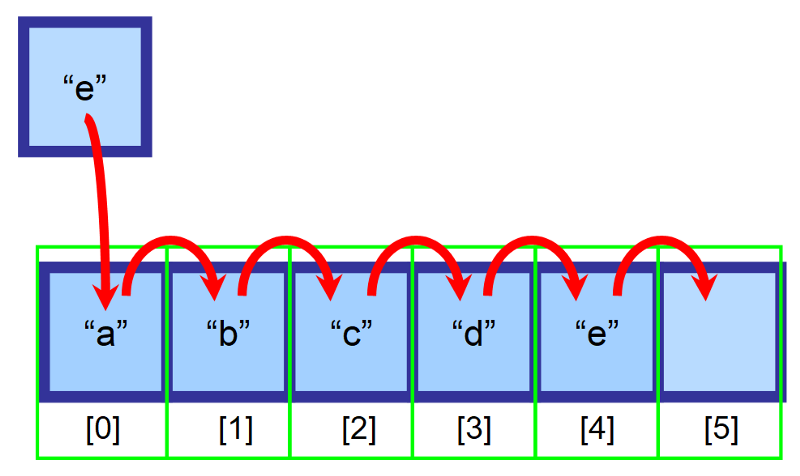
💡 Megjegyzés: Létre kell hoznunk egy változót, hogy nyomon követhessük az utolsó indexet, amely elemeket tartalmaz. A fenti ábrán a tömb a beszúrás előtt a 4-es indexig van feltöltve. Így meg tudjuk állapítani, hogy a tömb megtelt-e, és hogy melyik indexet kell használnunk ahhoz, hogy a végén beillesszünk egy elemet.

Azt követően, hogy ezt megtettük, az elemünk sikeresen beillesztésre került. 👏

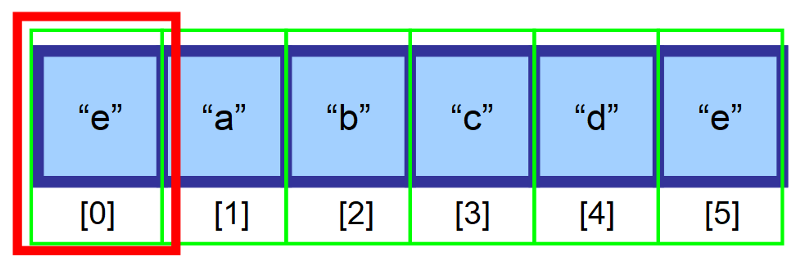
⚠️ Várjunk csak! Mi történik, ha a tömb megtelt?

Mit gondolsz, mi történik, ha a tömb megtelt, és megpróbálsz beszúrni egy elemet? 😱

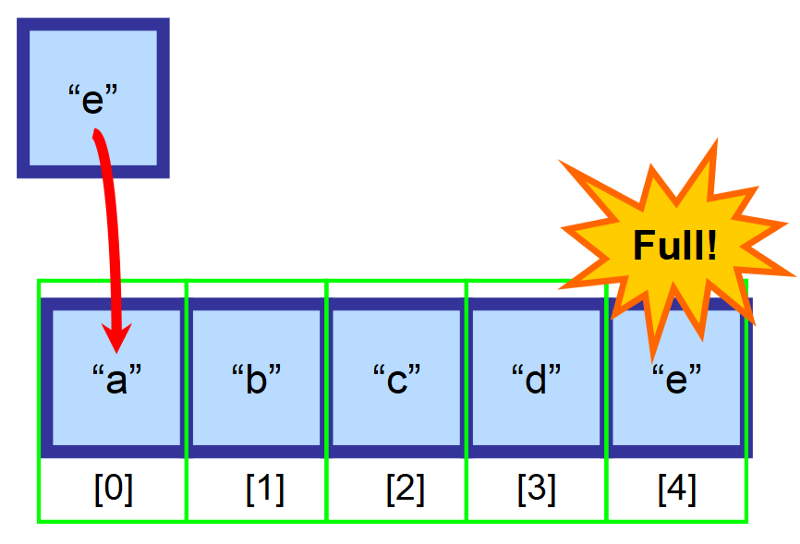
Ez esetben létre kell hoznod egy új, nagyobb tömböt, és az összes elemet kézzel át kell másolnod ebbe az új tömbbe. Ez a művelet idő szempontjából nagyon költséges. Képzeld el, mi történne, ha több millió elemű tömböd lenne! Ez nagyon sokáig tartana. ⏳

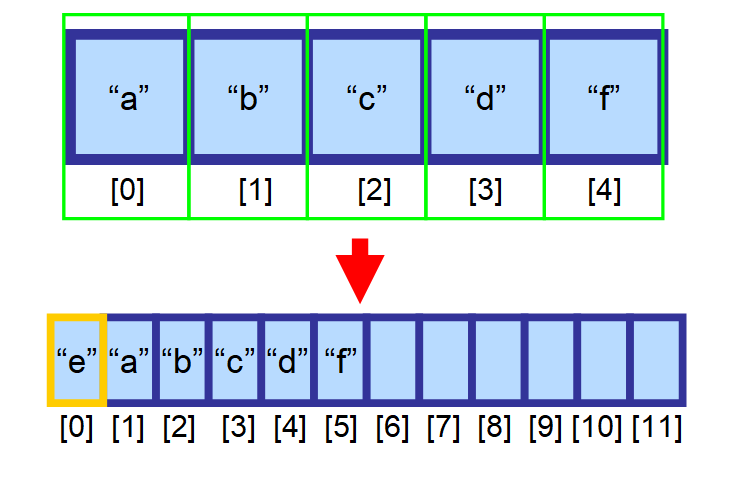
💡 Megjegyzés: Az egyetlen kivétel ez alól a szabály alól, amikor a beszúrás nagyon gyors, az az, amikor a tömb végén (az utolsó elemtől jobbra található indexnél) szúrunk be egy elemet, és még van szabad hely. Ez O(1) állandó idő alatt történik.

2️⃣ Törlés- Bye, Bye!

Tegyük fel, hogy törölni szeretnénk egy elemet a tömbből.

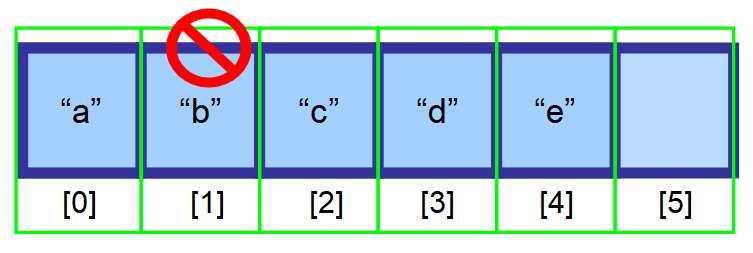
A véletlenszerű hozzáférés hatékonyságának fenntartása érdekében (hogy a tömböt egy indexen keresztül rendkívül gyorsan tudjuk elérni) az elemeket egybefüggő memóriaterületeken kell tárolni. Nem lehet csak úgy törölni az elemet, és üresen hagyni azt a helyet.

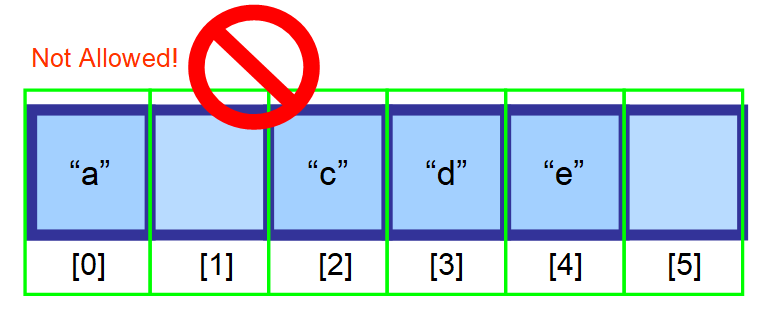
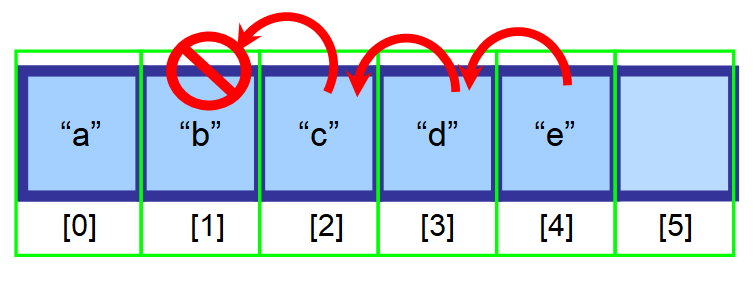
A törlendő elem után következő elemeket egy indexszel balra kell tolni.

És végül ez az eredményül kapott tömb 👇. Amint láthatod, a “b” sikeresen törlődött.

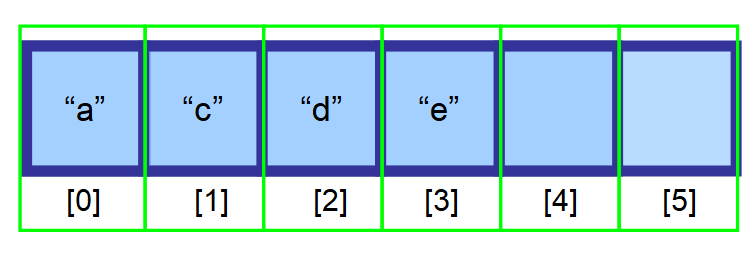
💡 Megjegyzés: A törlés nagyon hatékony, ha az utolsó elemet távolítod el. Mivel létre kell hoznunk egy változót, hogy nyomon kövessük az utolsó elemeket tartalmazó indexet (a fenti ábrán a 3. index), az index segítségével közvetlenül eltávolíthatjuk az adott elemet.

3️⃣ Elem keresése

Három lehetősége van egy elem megtalálására egy tömbben:

• Ha tudja, hogy hol található, használja az indexet.
• Ha nem tudja, hogy hol található, és az adatok rendezettek, akkor algoritmusokat használhat a keresés optimalizálására, például a bináris keresést.
• Ha nem tudja, hogy hol található, és az adatai nincsenek rendezve, akkor végig kell keresnie a tömb minden elemét, és meg kell vizsgálnia, hogy az aktuális elem a keresett elem-e (lásd az alábbi diagramok sorozatát).

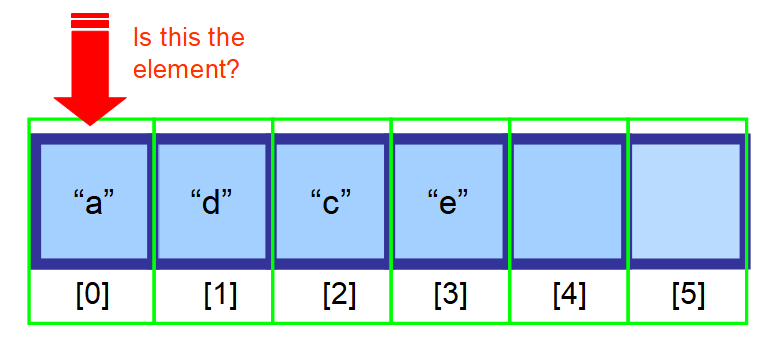
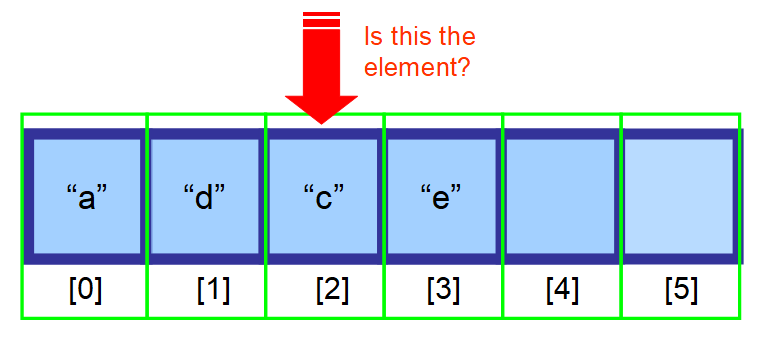
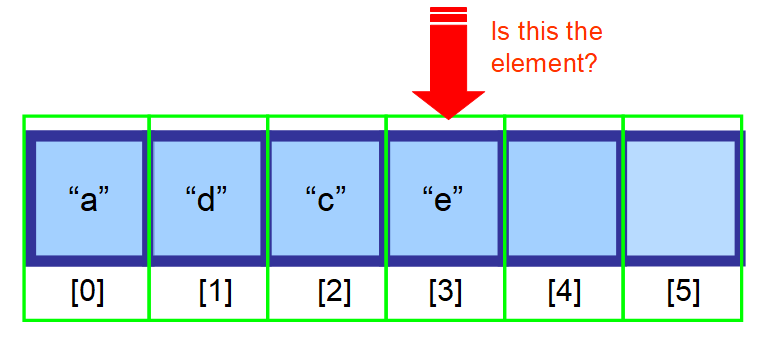
👋 Összefoglalva…

• A tömbök rendkívül hatékony adatszerkezetek, amelyek azonos típusú elemeket tárolnak. Az elemek típusa és a tömb mérete fix és meghatározott a létrehozásakor.
• A memória a tömb létrehozása után azonnal kiosztásra kerül, és az értékek hozzárendeléséig üres marad.
• Az elemek egybefüggő helyeken helyezkednek el a memóriában, így nagyon hatékonyan (véletlen hozzáférés, O(1) = állandó idő) elérhetők az indexek segítségével.
• Az indexek 0-val kezdődnek, nem 1-gyel, ahogy megszoktuk.
• A tömb elején vagy közepén lévő elemek beszúrása az elemek jobbra mozgatásával jár. Ha a tömb megtelt, egy új, nagyobb tömb létrehozása (ami nem túl hatékony). A tömb végén történő beszúrás nagyon hatékony, állandó ideje O(1).
• A tömb elején vagy közepén lévő elemek eltávolítása az összes elem balra mozgatásával jár, hogy ne maradjon üres hely a memóriában. Ez garantálja, hogy az elemek egybefüggő helyeken tárolódnak a memóriában. A tömb végén történő eltávolítás nagyon hatékony, mert csak az utolsó elemet töröljük.
• Egy elem megtalálásához az egész tömböt át kell vizsgálni, amíg meg nem találjuk. Ha az adatok rendezettek, akkor a folyamat optimalizálásához olyan algoritmusokat használhat, mint például a bináris keresés.

“Tanulj a tegnapból, élj a mának, reménykedj a holnapban. A legfontosabb, hogy ne hagyd abba a kérdezést.”
– Albert Einstein

👋 Köszönöm!

Nagyon remélem, hogy tetszett a cikkem. ❤️
Kövess engem a Twitteren, hogy még több ilyen cikket találj. 😃