Pour cette seconde partie, voir Horloges à eau
A l’époque des anciens Grecs et Romains, la terre était considérée comme le centre de l’univers, qui était lui-même une sphère contenant toutes les étoiles. Cette sphère céleste tournait d’est en ouest, portant non seulement les étoiles mais aussi le soleil et les planètes. Par conséquent, le soleil tournait autour de la terre. C’est ce qui a provoqué le jour et la nuit. La terre ne tournait pas. Pour comprendre les cadrans solaires, il est parfaitement acceptable et pratique d’adopter cette vision géocentrique. Le soleil ne se déplaçait pas autour de la terre dans un cercle perpendiculaire à l’axe de la terre (qui était aussi l’axe de la sphère céleste) comme le faisaient les étoiles. Au contraire, le soleil traçait un cercle le long de la sphère céleste, centré sur la terre, connu sous le nom d’écliptique.
Le plan écliptique rencontre le plan équatorial à environ 23,5°. C’est ce qu’on appelle l’obliquité de l’écliptique. Le cercle de l’écliptique coupe plus ou moins les douze constellations du zodiaque, et la période de l’année (correspondant aux mois modernes) était calculée en fonction du signe du zodiaque que traversait le soleil. (Quel que soit l’emplacement exact des constellations du zodiaque, l’écliptique était divisé en 12 arcs égaux de 30° chacun, laissant la plupart des constellations décentrées et souvent pas entièrement dans leur région désignée de 30°). Le mouvement du soleil le long du cercle écliptique dure une année (solaire). Le double mouvement du soleil (sur la sphère céleste et le long de l’écliptique) signifie que le soleil suit une trajectoire différente dans le ciel chaque jour. Du point de vue de l’hémisphère nord, en été, le soleil est plus haut dans le ciel et reste visible plus longtemps. Comme les anciens divisaient toujours la lumière du jour en douze heures égales, ces heures d’été étaient plus longues. En hiver, le soleil est plus bas dans le ciel et reste visible moins longtemps. Par conséquent, les heures d’hiver étaient également plus courtes.
Le temps dans le monde antique était d’abord mesuré par des événements naturels, tels que le lever et le coucher du soleil, et les heures de repas :-
Dans les premiers âges de Rome et même jusqu’au milieu du cinquième siècle après la fondation de la ville, aucune autre division du jour n’était connue que le lever, le coucher du soleil et le midi, qui étaient marqués par l’arrivée du Soleil entre la Rostra et un lieu appelé Graecostasis.
La plus grande source littéraire qui existe pour les cadrans solaires de la Grèce et de Rome est les Dix livres sur l’architecture de Vitruve, écrits vers 25 avant J.-C. Dans le livre 9, Vitruve donne une liste d’une variété de cadrans et de leurs inventeurs :-
Berosus le Chaldéen aurait inventé le semi-circulaire taillé dans un bloc carré et entaillé pour suivre l’inclinaison de la terre. L’hémisphère, ou scaphê, est attribué à Aristarque de Samos, et il a également inventé le disque sur un plan. L’araignée a été inventée par Eudoxe l’astronome ; certains disent par Apollonius. Le Plinthe ou Coffre, dont un exemple se trouve dans le Cirque de Flaminius, fut inventé par Scopinas de Syracuse ; Parmenion inventa le « Cadran solaire pour l’examen » ; Théodose et Andrias le cadran solaire « pour chaque climat, » Patrocles la hache, Dionysodorus le cône, Apollonius le carquois. Les hommes nommés ici en ont inventé d’autres, et beaucoup d’autres nous en ont laissé d’autres encore, comme le Spider-Cone, le Hollowed Plinth, et l’Antiboreus (« Opposé au Nord »). De plus, beaucoup ont laissé derrière eux des instructions écrites pour fabriquer des versions portables et suspendues de ces objets. Quiconque le souhaite peut trouver des informations supplémentaires dans leurs livres, pour autant qu’il sache comment installer un analemme.
L’analemme de Vitruve est le système de lignes et de courbes qui indiquent les heures et les mois changeants sur la face d’un cadran solaire. Le chapitre précédent est consacré à la détermination de l’analemme à partir de l’observation de l’ombre d’un gnomon à midi à l’équinoxe. (Le gnomon était le bâton vertical qui projetait son ombre sur la face du cadran. Selon la conception du cadran, on utilisait soit le côté de la longueur de l’ombre, soit la position de la pointe de l’ombre pour déterminer l’heure). Malheureusement, Vitruve termine sa discussion sur les cadrans solaires avec la liste donnée ci-dessus et écrit sur les horloges à eau pour le reste du livre 9.
Avant que les Grecs ne développent le cadran solaire dans les formes que Vitruve énumère, les civilisations plus anciennes de l’Égypte et de la Mésopotamie avaient des dispositifs de mesure de l’ombre dès 1500 avant JC.C. Bien que ce soit la date des plus anciens cadrans solaires conservés :-
… il est possible que les cadrans solaires aient été inventés dès le troisième millénaire, lorsque les prêtres égyptiens ont commencé à diviser la nuit et le jour chacun en douze parties égales.
Un texte funéraire de 1290 av, faisant référence à des événements astronomiques du XIXe siècle avant J.-C., donne des instructions sur la façon de construire un « bâton d’ombre »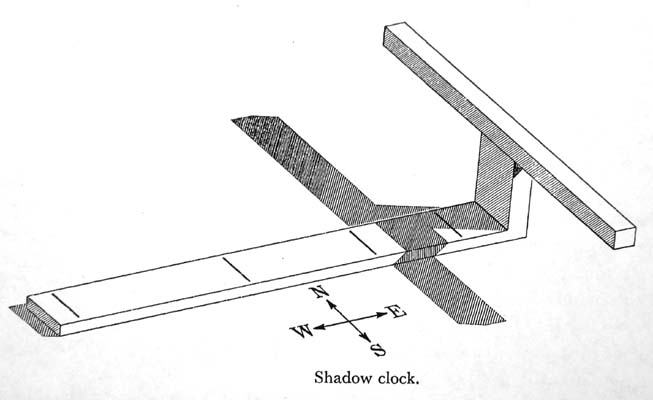
Cette horloge d’ombre consistait en une base avec un bâton vertical à une extrémité. En raison du décalage angulaire de l’ombre au cours de la journée, on a supposé que le bâton vertical avait une barre transversale ajoutée pour élargir l’ombre afin qu’elle tombe toujours sur l’horloge. Ni le texte funéraire ni les exemples survivants n’ont la barre transversale, bien qu’un spécimen ait des trous de chaque côté de son montant qui peuvent suggérer une telle addition.
En pratique, l’horloge d’ombre devait être tournée une fois par jour à midi afin de pouvoir marquer l’heure à la fois le matin et l’après-midi :-
Avec la tête à l’est 4 heures sont marquées par des longueurs d’ombre décroissantes après quoi l’instrument est inversé avec la tête à l’ouest pour marquer 4 heures d’après-midi.
Deux heures sont dites avoir eu lieu avant que le soleil ne frappe l’horloge le matin, et deux autres heures se sont écoulées après que le soleil ait quitté l’horloge mais avant que la nuit ne commence. L’hypothèse est que le crépuscule du matin avant le lever du soleil était compté comme une heure, et qu’une autre heure s’est écoulée entre le lever du soleil et le moment où le montant a projeté une ombre observable sur l’horloge. (L’ombre au lever du soleil serait d’une longueur infinie, et donc inutile pour marquer l’heure). Deux heures se sont également écoulées dans la soirée. Les marques sur l’horloge indiquant les quatre heures étaient très imprécises, et n’étaient peut-être pas basées sur l’observation mais plutôt sur une erreur de géométrie céleste.
Des cadrans solaires ressemblant à ceux dont parle Vitruve étaient utilisés en Égypte depuis au moins 1200 avant J.-C. Il s’agissait de cadrans solaires verticaux suspendus, de forme semi-circulaire avec un gnomon horizontal au sommet et au centre. « L’ombre balayait le cadran plus rapidement en début de matinée et en fin d’après-midi qu’à midi, mais les Égyptiens divisaient simplement le cadran en 12 secteurs de 15° ou ‘heures’. Il s’agit peut-être de l’ordre le plus rudimentaire d’utilisation du gnomon et il ne présente guère d’intérêt théorique ou empirique pour les Grecs. » La poursuite du développement égyptien dans le domaine de la mesure du temps semble s’être essoufflée jusqu’à l’invasion assyrienne au VIIe siècle avant J.-C.
Un cadran solaire presque complet a été découvert à Kantara, en Égypte, datant d’environ 320 avant J.-C., soit bien plus de mille ans après que les horloges d’ombre aient été en service :-

Le gnomon était un bloc perpendiculaire s’élevant au pied de la face inclinée, sa hauteur et sa largeur étant les mêmes que celles de cette dernière. Sur un côté se trouvait un dispositif permettant de suspendre un plumet de manière à le faire basculer librement de la base. L’instrument était posé sur une surface plane et, lorsqu’il devait être utilisé, il était tourné de manière à faire face directement au soleil. L’ombre du gnomon tombait alors sur sa face. Les espaces délimités par les lignes parallèles allant de haut en bas de la face indiquaient l’endroit où l’ombre devait être lue au cours des différents mois de l’année, en commençant par le solstice d’été à un bord et en revenant en arrière avec le solstice d’hiver à l’autre.
Le long de la face se trouvait un ensemble de lignes tracées obliquement et inclinées du bord du solstice d’hiver au bord du solstice d’été.
À six heures du matin, l’ombre frappait le haut du cadran ; à mesure que le soleil montait plus haut, l’ombre diminuait en longueur jusqu’à ce qu’à midi elle touche la ligne la plus basse ; elle atteignait à nouveau le haut du cadran à six heures du soir.
Ce cadran solaire et d’autres de conception similaire qui subsistent aujourd’hui ne sont pas terriblement précis :-
Certaines modifications auraient été nécessaires pour qu’ils donnent l’heure exacte. Une partie de cette inexactitude peut être due au fait qu’ils étaient des représentations d’instruments plus grands ou plus précis, bien que les cadrans de ce type devaient être soit assez petits pour être manipulés, soit avoir une sorte d’arrangement permettant de les tourner facilement.
Dans le monde grec, les premiers cadrans solaires « consistaient en un gnomon sous la forme d’un poteau ou d’un piquet vertical placé dans une surface plane, sur laquelle l’ombre du gnomon servait à indiquer l’heure ». Ce système s’oppose aux modèles modernes dont le gnomon est incliné parallèlement à l’axe de la Terre. Dans ce système moderne, les lignes du cadran indiquant les heures partent d’un point central et restent droites. C’est l’ombre du bord du gnomon situé sur ces lignes qui donne l’heure. Les variations saisonnières sont pratiquement insignifiantes :-
Dans les anciens cadrans à gnomon vertical, la direction de l’ombre à un moment donné de la journée variait avec les saisons. C’est donc la position de la pointe de l’ombre qui était essentielle à la détermination de l’heure. La pointe de l’ombre traçait une courbe sur le plan du cadran au fur et à mesure que le soleil se déplaçait, une courbe qui changeait de l’été à l’hiver.
Les courbes tracées sur le cadran d’un tel cadran solaire ont peut-être conduit à la découverte des sections coniques, attribuées à Menaechmus au quatrième siècle avant J.-C.
Le soleil trace une trajectoire circulaire dans le ciel dans son mouvement quotidien. La pointe du gnomon est le sommet d’un cône dont les rayons du soleil sont les éléments, et comme le plan du cadran coupe le cône, la trajectoire de l’ombre est une section conique. Si Ménaechme ou quelqu’un d’autre marquait ce trajet avec une série de points un jour donné, il » découvrirait » une hyperbole.
Il faut noter que les courbes solsticiales ne sont que des hyperboles entre les cercles arctique et antarctique. La courbe équinoxiale est une droite à toutes les latitudes sauf aux pôles. Les lignes solsticiales aux cercles arctique et antarctique seraient des paraboles et à l’intérieur des cercles, elles seraient des ellipses. L’ellipse est facile à voir car pendant la journée arctique, le soleil fait son circuit complet au-dessus de l’horizon, et donc l’ombre d’un gnomon tracerait la section conique fermée.
Les trajectoires de la pointe de l’ombre du gnomon tracées sur ces cadrans solaires horizontaux formaient un motif ressemblant à une hache appelé pelekinon (dérivé du mot grec pour hache).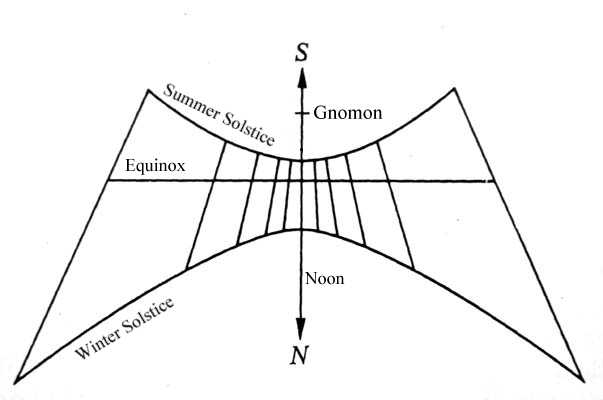
Le motif se composait d’une hyperbole traçant la trajectoire de l’ombre au solstice d’hiver, d’une seconde pour le solstice d’été, et d’une ligne droite est-ouest entre les deux marquant les ombres équinoxiales. Une ligne partant de la base du gnomon au sud du cadran et allant plein nord indiquait l’heure de midi. (Comme l’ombre de la pointe du gnomon était le dispositif d’indication de l’heure, le gnomon pouvait être incliné. L’angle du gnomon n’est pas pertinent. Dans un tel cadran, la ligne de midi partirait de la base d’une ligne perpendiculaire entre la pointe du gnomon et la surface du cadran). Les hyperboles étaient centrées sur cette ligne de midi. L’hyperbole d’hiver s’ouvrait au nord, l’hyperbole d’été au sud (en supposant que le cadran se trouve dans l’hémisphère nord). En plus de la ligne centrale de midi, des lignes obliques supplémentaires étaient ajoutées de chaque côté pour indiquer les heures de jour avant et après midi :-
Il est évident, d’après les exemples conservés de cadrans horizontaux, que les lignes droites qui relient les points horaires du solstice d’été, de l’équinoxe et du solstice d’hiver servaient à approximer ces lignes horaires dans l’antiquité gréco-romaine.
En outre :-
… les courbes du jour solsticial sur presque tous les cadrans horizontaux conservés ont été approximées par des lignes brisées qui relient les points horaires. Cela semble indiquer que le dialer a localisé ces points horaires sur la face du cadran avant de graver les courbes du jour.
On ne sait toujours pas si certains, sinon tous, cadrans solaires de ce type ont été dessinés par observation ou par calcul. Il existe des preuves qui suggèrent que des méthodes de projection étaient utilisées pour déterminer les points des heures :-
Vitruve et Ptolémée décrivent tous deux des analemmes qui, pour des positions solaires données, servent à déterminer la longueur et la direction de l’ombre projetée par un gnomon sur la face d’un cadran solaire plan.
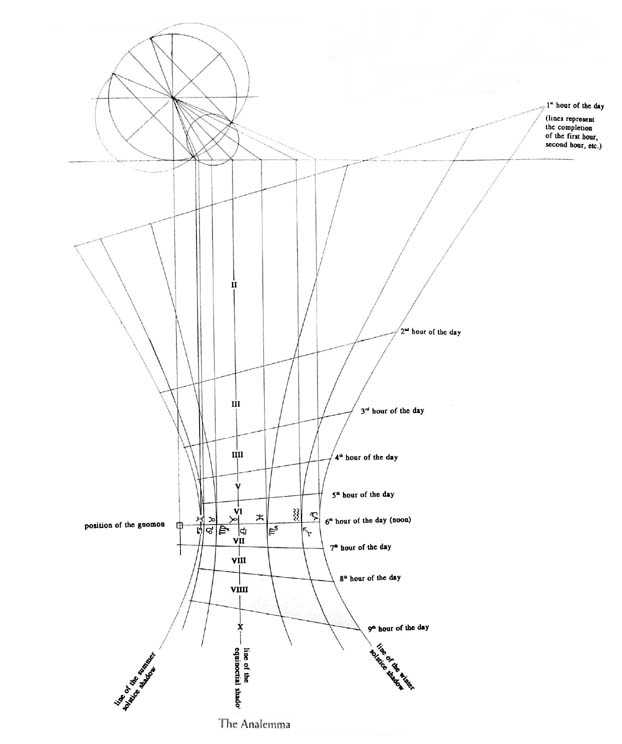
Spécifiquement, dans son livre, « Sur l’analemme », Ptolémée donne des méthodes pour dériver, à la fois par des moyens trigonométriques et aussi par des moyens graphiques, trois paires de coordonnées sphériques pour le soleil par rapport à un lieu donné sur la terre, donné la déclinaison solaire, la latitude terrestre, et l’heure du jour. Bien qu’il ne le dise pas explicitement, chaque paire de coordonnées sphériques est singulièrement adaptée pour trouver la longueur et la direction de l’ombre d’un gnomon pour un type de cadran solaire plan.
Pour compliquer les choses, les spécifications exactes du réseau de courbes d’un cadran solaire variaient en fonction de la latitude du cadran. Si des moyens mathématiques étaient utilisés pour créer le motif d’un cadran solaire, on devrait s’attendre à ce que la latitude prévue soit prise en compte. Cependant, on a trouvé des cadrans solaires à des latitudes qui variaient jusqu’à 7 degrés de latitude (soit une distance de plus de 700 kilomètres). L’exemple le plus significatif d’une telle divergence est le cadran solaire qui fut la première pièce d’horlogerie officielle de Rome. Les Romains ont capturé un cadran solaire lors d’une guerre en Sicile en 264 avant J.-C. Malgré la différence d’environ 4 degrés de latitude, le cadran solaire a servi à Rome pendant près de cent ans avant qu’un nouveau cadran calibré pour la ville ne soit mis en place. Ceci malgré une erreur observable de l’heure :-
Bien que l’ombre d’un bâton dans le sol semble être la forme la plus simple de garde-temps, le cadran horizontal est plus complexe à délimiter dans les espaces horaires pour le système d’heure temporaire que ne le sont les cadrans de section sphérique ou conique… puisqu’une compréhension de base des origines des trajectoires hyperboliques de l’ombre sur la surface plane est nécessaire pour adapter la figure géométrique nécessaire à sa réalisation.
La figure géométrique est l’analemme dont Vitruve a parlé plus haut. L’analemme est la:-
… projection de la sphère céleste dans un plan, à partir duquel à son tour les positions des heures sur la surface du cadran ont été déduites. Vitruve décrit la figure de base … bien que son texte à ce point soit quelque peu obscur et qu’il pourrait bien ne pas avoir clairement compris ce qu’il décrivait de toute façon.
Après avoir décrit comment la ligne équinoxiale peut être trouvée, ainsi que le point de midi aux solstices, Vitruve termine ses réflexions sur l’analemme comme suit :-
Si la construction initiale demandait un plus grand effort, la facilité avec laquelle les lignes du jour et de l’heure pouvaient être tracées a rendu les cadrans solaires sphériques dans l’Antiquité plus populaires que leurs homologues plats. Le principe de base du cadran solaire sphérique était de refléter la sphère céleste dans laquelle le soleil se déplace. La construction de base consistait à creuser un hémisphère (ou un petit coin de sphère) dont le sommet était parallèle à l’horizon. Un gnomon était placé de façon à ce que sa pointe soit au centre de l’hémisphère, au même niveau que le plan de l’horizon. Un jour donné, l’ombre projetée par la pointe du gnomon traçait l’arc d’un cercle sur la surface du cadran.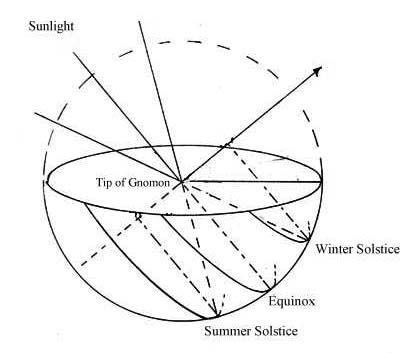
L’arc du solstice d’été était le plus éloigné vers le bas de l’hémisphère. Lorsque les saisons se déplaçaient vers l’hiver, ces arcs étaient de plus en plus proches du bord supérieur de l’hémisphère. Ces arcs quotidiens étaient tous parallèles, et l’arc de l’équinoxe était la moitié d’un cercle dont le centre était le même que celui de l’hémisphère (un grand cercle). Les lignes horaires n’étaient pas des courbes circulaires, à l’exception de celles situées aux horizons (marquant le lever et le coucher du soleil) et de la ligne de midi. Malgré leur nature non circulaire, pour les latitudes inférieures à 45°, les lignes horaires saisonnières entre le méridien et l’horizon sont très proches des grands cercles qui passent par les points horaires saisonniers correspondants sur les courbes solsticiales et équinoxiales. Les lignes horaires gravées sur les cadrans solaires sphériques conservés semblent être de telles approximations de grands cercles. La déviation des lignes horaires par rapport aux grands cercles ne peut même pas être détectée sur les quelques cadrans où plus de trois courbes diurnes ont été divisées.Ainsi, le marquage des lignes horaires ne nécessitait ni observations minutieuses ni mathématiques compliquées. Il suffisait de diviser la surface de l’hémisphère qui recevait l’ombre du gnomon en douze parties égales à l’aide de grands cercles, de la même manière qu’un globe moderne est divisé en lignes de longitude. Pour simplifier encore plus le cadran sphérique, les courbes des jours n’avaient pas besoin de correspondre aux équinoxes ou aux solstices si le cadran avait pour seul but de servir d’horloge. Deux ou trois arcs de cercle parallèles étaient suffisants pour faciliter la lecture (étant les lignes de « latitude » correspondantes). Plusieurs exemples de ces cadrans ont été trouvés dans des sites tels que Pompéi, Herculanum, Ostie et Rome. C’est seulement lorsque le cadran devait servir de calendrier que ces lignes devaient correspondre aux équinoxes et aux solstices.
Pour cette deuxième partie, voir Horloges à eau
.
