Waldin testi: Määritelmä, esimerkkejä, testin suorittaminen

Hypoteesin testaus > Waldin testi

Mikä on Waldin testi?

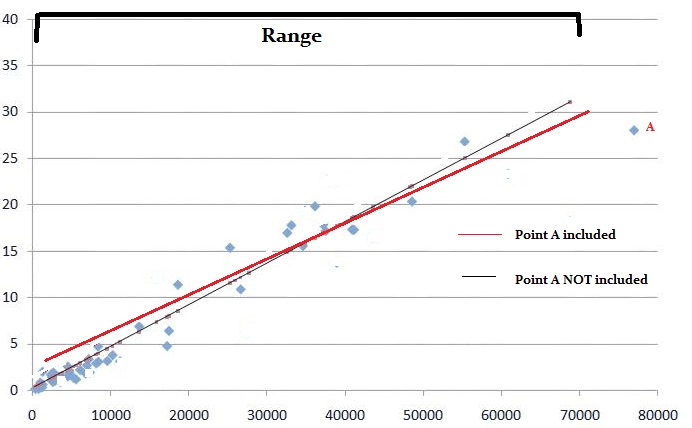
Wald-testi voi kertoa, mitkä mallin muuttujat vaikuttavat johonkin merkittävään.

Wald-testillä (jota kutsutaan myös Waldin chi-neliötestiksi) voidaan selvittää, ovatko mallin selittävät muuttujat merkittäviä. ”Merkitsevä” tarkoittaa, että ne lisäävät jotain malliin; muuttujat, jotka eivät lisää mitään, voidaan poistaa vaikuttamatta malliin millään merkityksellisellä tavalla. Testiä voidaan käyttää monille erilaisille malleille, myös sellaisille, joissa on binäärimuuttujia tai jatkuvia muuttujia.
Testin nollahypoteesi on: jokin parametri = jokin arvo. Voit esimerkiksi tutkia, vaikuttaako roskaruoan syöminen kaksi kertaa viikossa painoon. ”Paino” olisi parametrisi. Arvo voisi olla nolla (osoittaen, että roskaruoan syöminen ei mielestäsi vaikuta painoon). Jos nollahypoteesi hylätään, se viittaa siihen, että kyseiset muuttujat voidaan poistaa ilman suurta haittaa mallin sopivuudelle.

• Jos Waldin testi osoittaa, että tiettyjen selittävien muuttujien parametrit ovat nolla, voit poistaa muuttujat mallista.
• Jos testi osoittaa, että parametrit eivät ole nolla, muuttujat kannattaa sisällyttää malliin.

Wald-testistä puhutaan yleensä khiin neliöinä, koska otantajakauma (n:n lähestyessä ääretöntä) on yleensä tunnettu. Tätä testin muunnelmaa kutsutaan joskus Waldin khiin neliö -testiksi erotukseksi Waldin log-lineaarisesta khiin neliö -testistä, joka on ei-parametrinen muunnelma, joka perustuu log-kertoimen suhdelukuihin.

Vertailu muihin testeihin

Waldin testi on karkea approksimaatio Likelihood Ratio -testistä. Se voidaan kuitenkin suorittaa yhdellä mallilla (LR-testi vaatii vähintään kaksi mallia). Se on myös laajemmin sovellettavissa kuin LRT-testi: usein Wald-testin voi suorittaa tilanteissa, joissa mitään muuta testiä ei voi suorittaa.

Suurille n:n arvoille Wald-testi vastaa suunnilleen t-testiä; molemmat testit hylkäävät samat arvot suurilla otoskoolla. Waldin, LRT:n ja Lagrangen kertoimen testit ovat kaikki ekvivalentteja, kun otoskoko lähestyy ääretöntä (kutsutaan ”asymptoottisesti ekvivalentiksi”). Kuitenkin äärellisen kokoiset otokset, erityisesti pienemmät otokset, antavat todennäköisesti hyvin erilaisia tuloksia.

Agresti (1990) ehdottaa, että kannattaa käyttää LRT-testiä Wald-testin sijasta, jos otoskoko on pieni tai jos parametrit ovat suuria. ”Pieni” otoskoko on alle noin 30.

Testin suorittaminen

Tarvitsetko apua kotitehtäväkysymykseen? Käy tutorointisivullamme!

Wald-testin tilastokaava on: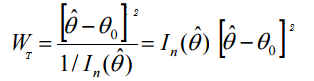

Jossa:

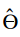• = Maximum Likelihood Estimator (MLE),
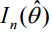• = odotettavissa oleva Fisherin informaatio (arvioitu MLE:llä).

Periaatteessa testi etsii eroja: Θ0 – Θ. Yleiset vaiheet ovat:

1. Etsitään MLE.
2. Etsitään odotettu Fisherin informaatio.
3. Arvioidaan Fisherin informaatio MLE:llä.

Myös MLE:n ja Fisherin informaation yhdistelmällä Wald-testin työstäminen on hyvin monimutkaista eikä sitä yleensä lasketa käsin. Monet ohjelmistot voivat suorittaa testin.

• Stata: käytä test-komentoa.
• R: katso Toronton yliopiston WALD-testin ohjeet R:lle (ladattavissa PDF-tiedostona).
• SAS: käytä TEST-lausetta. WALD on oletusarvo, jos testiä ei ole määritetty.

Viite:
Agresti A. (1990) Kategoristen tietojen analyysi. John Wiley and Sons, New York.

——————————————————————————

Tarvitsetko apua kotitehtävän tai kokeen kysymyksen kanssa? Chegg Studyn avulla saat kysymyksiisi vaiheittaiset ratkaisut alan asiantuntijalta. Ensimmäiset 30 minuuttia Chegg-opettajan kanssa ovat ilmaisia!