Tietorakenteet 101: Array – Visuaalinen johdatus aloittelijoille

Tutustu tietorakenteisiin, joita käytät päivittäin.

👋 Tervetuloa! Aloitetaan elintärkeällä kontekstilla. Sallikaa minun kysyä teiltä tämä:
✅ Kuunteletko musiikkia älypuhelimellasi?
✅ Pidätkö puhelimessasi yhteystietoluetteloa?
✅ Oletko koskaan nähnyt tulostaulukkoa kilpailun aikana?

Jos vastauksesi on ”kyllä” johonkin näistä kysymyksistä, on lähes varmaa, että olet käyttänyt taulukkomuotoiluja etkä edes tiennyt sitä! 😃 Joukot ovat erittäin tehokkaita tietorakenteita, jotka tallentavat elementtiluetteloita. Niillä on loputtomasti sovelluksia. Ne ovat erittäin tärkeitä tietotekniikan maailmassa.

Tässä artikkelissa opit matriisien hyvät ja huonot puolet, niiden rakenteen, operaatiot ja käyttötapaukset.

Aloitetaan! 👍

🔎 Syväsukellus arrayjen perusrakenteeseen

Ymmärtääksesi, miten ne toimivat, on erittäin hyödyllistä visualisoida tietokoneen muisti ruudukkona, kuten alla olevassa kuvassa. Jokainen tieto on tallennettu yhteen noista pienistä elementeistä (neliöistä), jotka muodostavat ruudukon.

Arrayissä hyödynnetään tätä ”ruudukkorakennetta” ja tallennetaan toisiinsa liittyvien tietojen luettelot vierekkäisiin muistipaikkoihin, jotta voidaan taata äärimmäinen tehokkuus näiden arvojen löytämisessä. 🔳🔳🔳🔳 🔳

Voit ajatella matriiseja näin:

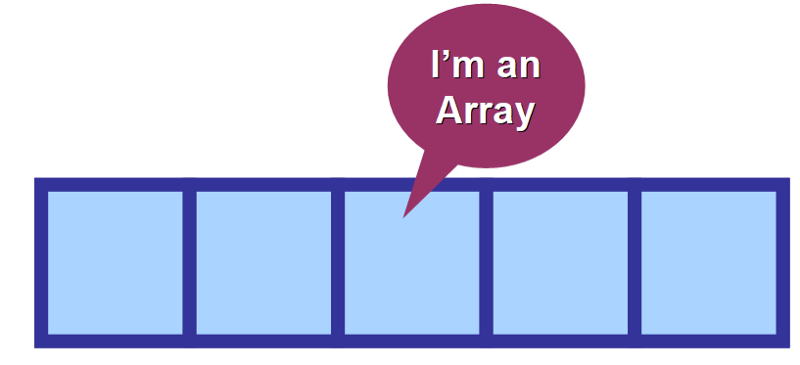
Sen elementit ovat vierekkäin muistissa. Jos joudut käyttämään useampaa kuin yhtä niistä, prosessi on äärimmäisen optimoitu, koska tietokone tietää jo valmiiksi, missä arvo sijaitsee.

Hienoa, eikö? Opetellaanpa, miten tämä toimii kulissien takana! 😃

📚 Luokittelu

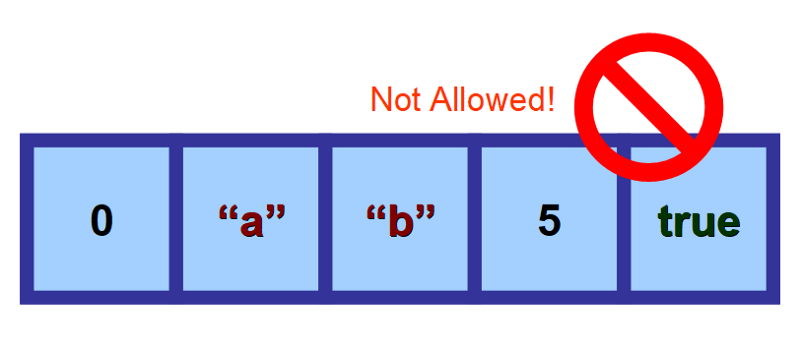
Jonot luokitellaan homogeenisiksi tietorakenteiksi, koska ne tallentavat samantyyppisiä elementtejä.

Näihin voidaan tallentaa numeroita, merkkijonoja, boolean-arvoja (tosi ja epätosi), merkkejä, objekteja ja niin edelleen. Mutta kun olet määrittänyt, minkä tyyppisiä arvoja joukkoosi tallentaa, kaikkien sen elementtien on oltava samaa tyyppiä. Et voi ”sekoittaa” eri tietotyyppejä.

👀 Arvojen lukeminen – taika alkaa!

Matriisien hämmästyttävä voima tulee niiden tehokkuudesta käyttää arvoja. Tämä saavutetaan sen ruudukkomaisen rakenteen ansiosta. Katsotaanpa tätä tarkemmin.🔍

Kun luot array:
– Määrität sen muuttujaan. 👈
– Määrität, minkä tyyppisiä elementtejä se tallentaa. 🎈
– Määrität sen koon (elementtien enimmäismäärän). 📚

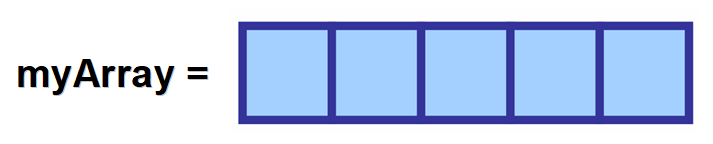
💡 Huomautus: Nimi, jonka annat tälle muuttujalle, on erittäin tärkeä, koska käytät sitä myöhemmin koodissasi arvojen käyttämiseen ja matriisin muuttamiseen.

Mutta miten voit kertoa tietokoneelle, mitä tiettyä arvoa haluat käyttää? Tässä kohtaa indeksit ovat tärkeässä roolissa!

1️⃣ Indeksit

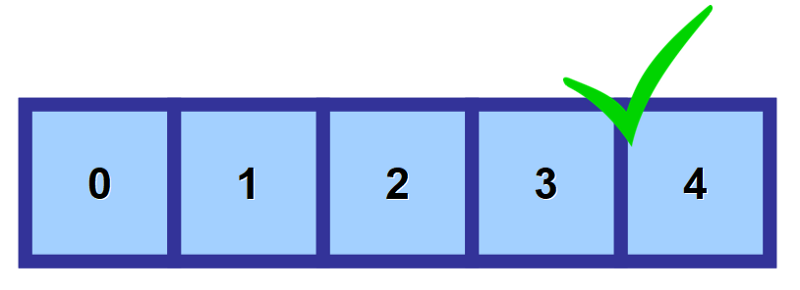
Käytät niin sanottua ”indeksiä” (”indeksejä” monikossa) päästäksesi käsiksi johonkin arvoon matriisissa. Se on numero, joka viittaa paikkaan, johon arvo on tallennettu.

Kuten näet alla olevasta kaaviosta, matriisin ensimmäiseen elementtiin viitataan indeksillä 0. Kun siirryt eteenpäin oikealle, indeksi kasvaa yhdellä jokaista muistipaikkaa kohti.

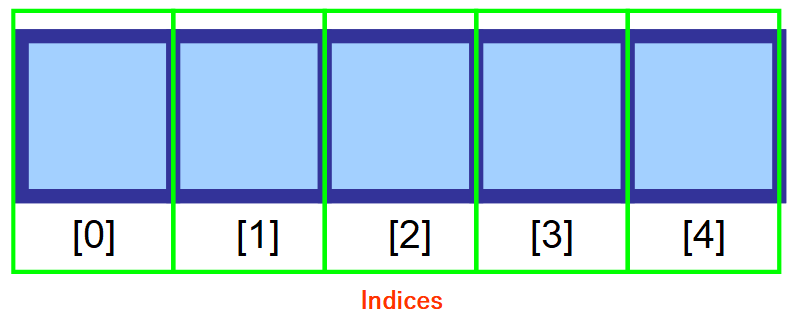
💡 Huomautus: Tiedän, että aluksi tuntuu oudolta aloittaa laskenta 0:sta eikä 1:stä, mutta tätä kutsutaan nollapohjaiseksi numeroinniksi. Se on hyvin yleistä tietotekniikassa.

Yleinen syntaksi elementin käyttämiseksi on: <ArrayVariable>

Esimerkiksi:
Jos joukkosi on tallennettu muuttujaan myArray ja haluat päästä käsiksi ensimmäiseen elementtiin (indeksillä 0), käyttäisit myArray

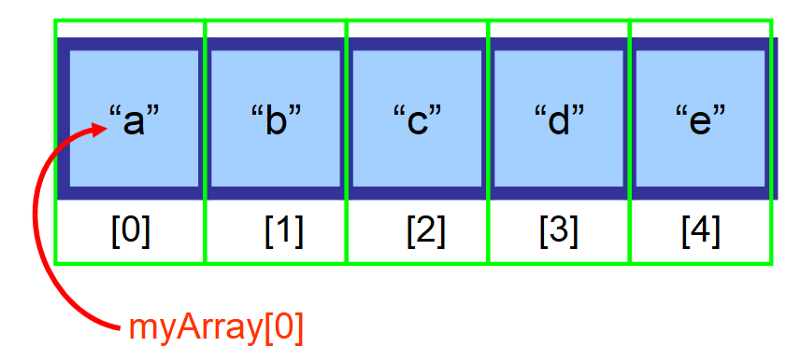
2️⃣ Muisti

Nyt kun tiedät, miten arvoihin päästään käsiksi, katsotaanpa, miten joukkoja tallennetaan tietokoneen muistiin. Kun määrittelet matriisin koon, koko tuo tila muistissa ”varataan” siitä hetkestä lähtien tulevia arvoja varten, joita haluat mahdollisesti lisätä.

💡 Huomaa: Jos et täytä matriisia arvoilla, tuo tila pysyy varattuna ja tyhjänä, kunnes täytät sen.

Esimerkki:
Esitettäkö, että määrittelet matriisin, jonka koko on 5, mutta lisäät sinne vain yhden arvon. Kaikki tuo jäljelle jäävä tila jää tyhjäksi ja ”varataan” muistiin odottamaan tulevia osoituksia.

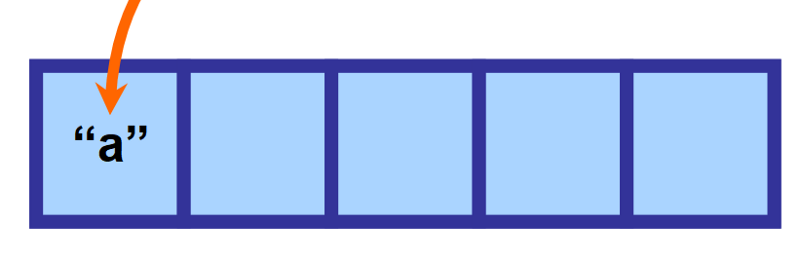
Tämä on avainasemassa, koska matriisit ovat erittäin tehokkaita arvojen käyttämisessä, koska kaikki elementit on tallennettu vierekkäisiin tiloihin muistissa. Näin tietokone tietää tarkalleen, mistä etsiä pyytämäsi tiedot.

Mutta… siinä on kääntöpuolensa 😞 koska tämä ei ole muistitehokasta. Varaat muistia tulevia toimintoja varten, joita ei ehkä tapahdu. Siksi matriiseja suositellaan tilanteissa, joissa tiedät etukäteen, kuinka monta elementtiä aiot tallentaa.

🔧 Operaatiot – Kulissien takana!

Nyt kun tiedät, mitä matriisit ovat, kun niitä käytetään, ja miten ne tallentavat elementtejä, sukellamme niiden operaatioihin, kuten lisäykseen ja poistoon.

1️⃣ Lisäys – Tervetuloa!

Tiedetään, että meillä on 6-kokoinen matriisi ja siinä on vielä tyhjää tilaa. Haluamme lisätä elementin ”e” matriisin alkuun (indeksi 0), mutta tämä paikka on jo varattu elementillä ”a”. Mitä meidän pitäisi tehdä?

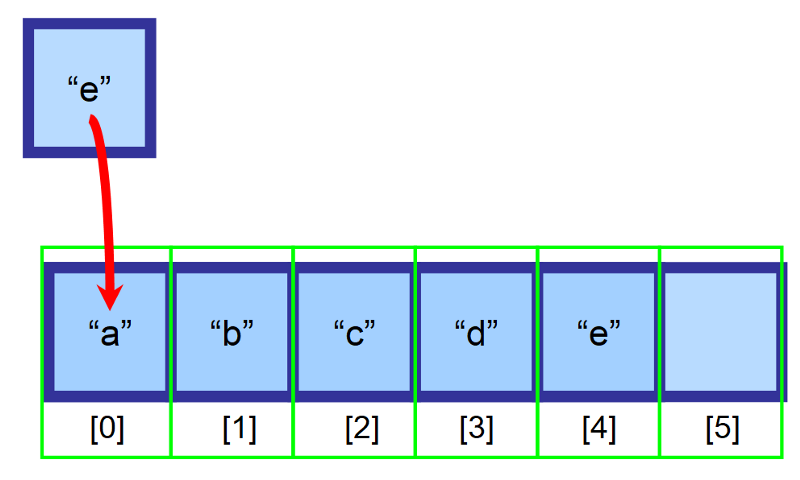
Sisällyttääksemme matriisiin siirretään kaikki elementit, jotka sijaitsevat lisäämiskohdan oikealla puolella, yhden indeksin verran oikealle. Elementti ”a” on nyt indeksissä 1, elementti ”b” indeksissä 2 ja niin edelleen…

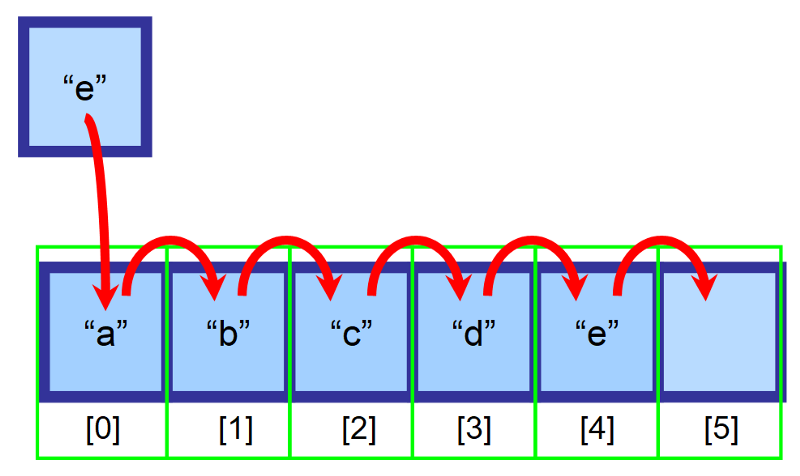
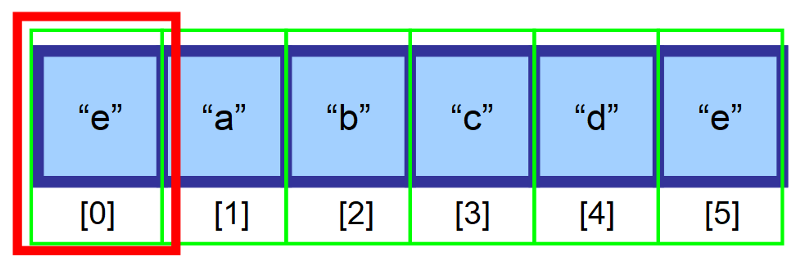
💡 Huomautus: Sinun on luotava muuttuja, joka pitää kirjaa viimeisestä indeksistä, joka sisältää elementtejä. Yllä olevassa kaaviossa array on täytetty indeksiin 4 asti ennen lisäystä. Näin voit määrittää, onko array täynnä ja mitä indeksiä sinun pitäisi käyttää lisätessäsi elementin lopussa.

Tämän jälkeen elementtimme on onnistuneesti lisätty. 👏

⚠️ Hetkinen! Mitä tapahtuu, jos array on täynnä?

Mitä luulet tapahtuvan, jos array on täynnä ja yrität lisätä elementin? 😱

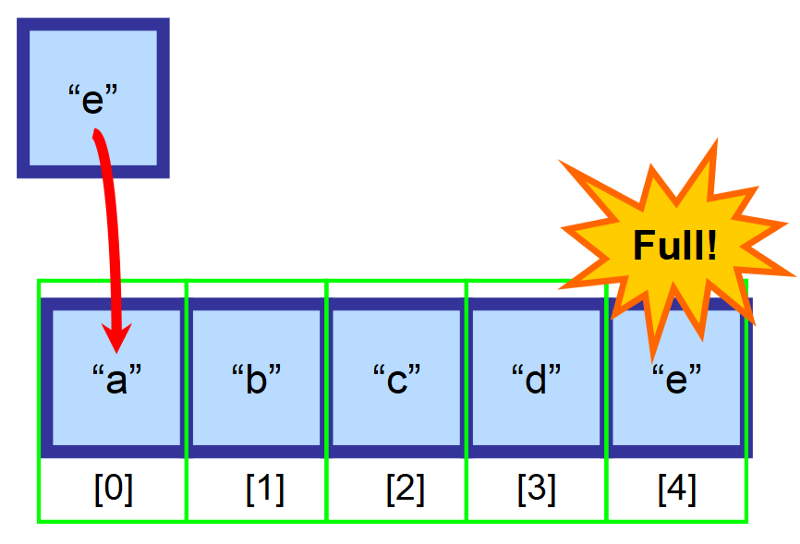
Tällöin sinun on luotava uusi, suurempi array ja kopioitava kaikki elementit käsin tähän uuteen arrayyn. Tämä toimenpide on ajallisesti hyvin kallis. Kuvittele, mitä tapahtuisi, jos sinulla olisi miljoonia elementtejä sisältävä array! Se voisi kestää hyvin kauan. ⏳

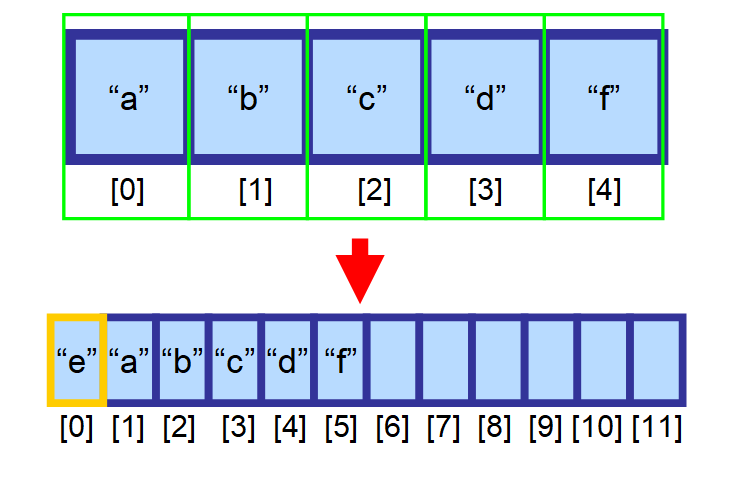
💡 Huomautus: Ainoa poikkeus tähän sääntöön, jolloin lisääminen on hyvin nopeaa, on silloin, kun lisäät elementin joukon loppuun (viimeisen elementin oikealla puolella olevaan indeksiin) ja tilaa on vielä jäljellä. Tämä tapahtuu vakioajassa O(1).

2️⃣ Poistaminen- Heippa, heippa!

Sitotaan nyt, että halutaan poistaa elementti joukosta.

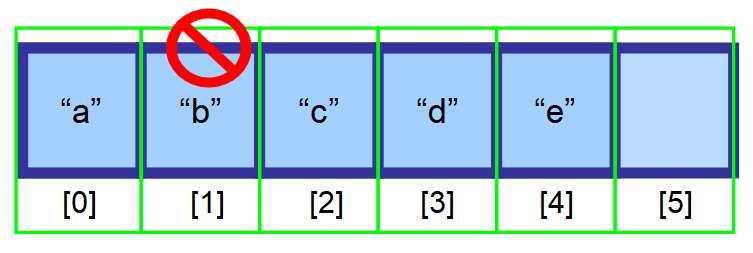
Jotta satunnaiskäytön tehokkuus säilyisi ennallaan (jotta joukkoon päästään indeksin kautta äärimmäisen nopeasti), elementit on tallennettava muistin vierekkäisiin tiloihin. Et voi vain poistaa elementtiä ja jättää kyseistä tilaa tyhjäksi.

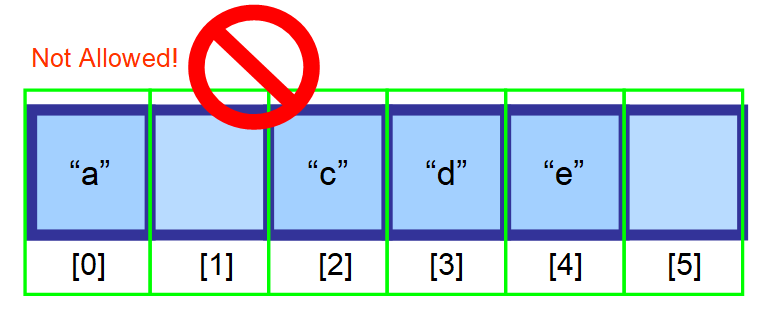
Siitä elementtejä, jotka tulevat sen elementin jälkeen, jonka haluat poistaa, pitää siirtää yksi indeksi vasemmalle.

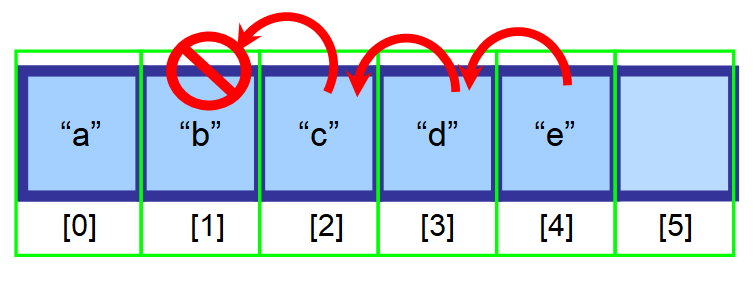
Viimein sinulla on tämä tuloksena oleva array 👇. Kuten näet, ”b” on onnistuneesti poistettu.

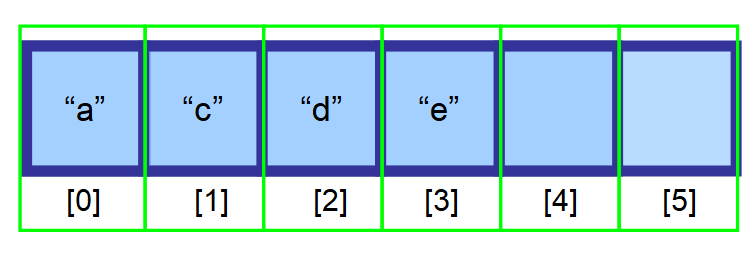
💡 Huomautus: Poistaminen on erittäin tehokasta, kun poistat viimeisen elementin. Koska sinun on luotava muuttuja, joka pitää kirjaa viimeisestä indeksistä, joka sisältää elementtejä (yllä olevassa kaaviossa indeksi 3), voit poistaa kyseisen elementin suoraan indeksin avulla.

3️⃣ Elementin etsiminen

Sinulla on kolme vaihtoehtoa löytää elementti joukosta:

• Jos tiedät, missä se sijaitsee, käytä indeksiä.
• Jos et tiedä, missä se sijaitsee, ja tietosi ovat lajiteltuja, voit käyttää algoritmeja haun optimoimiseksi, kuten Binary Search.
• Jos et tiedä, missä se sijaitsee, ja tietosi eivät ole lajiteltuja, sinun on etsittävä kaikki matriisin elementit läpi ja tarkistettava, onko nykyinen elementti etsimäsi elementti (katso alla oleva kaaviojakso).

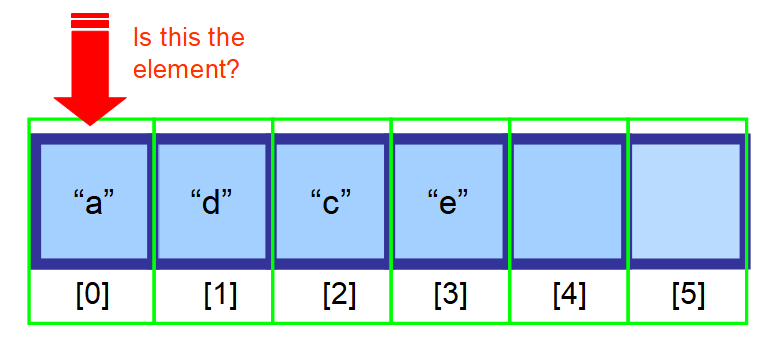
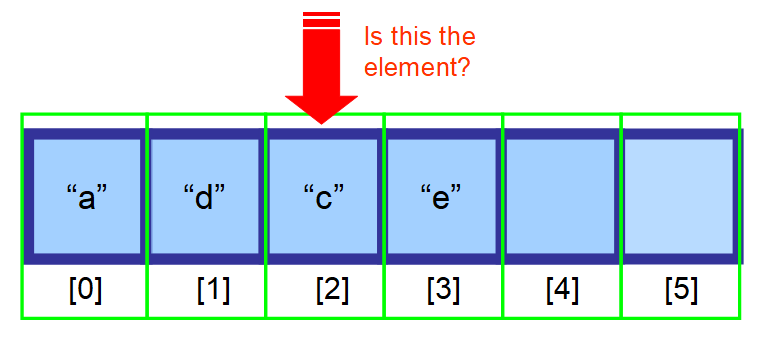
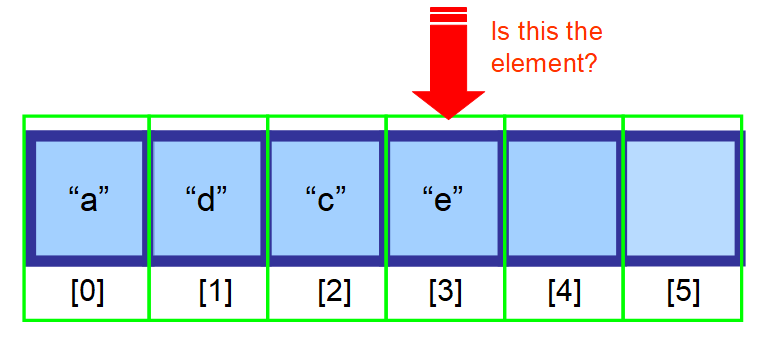
👋 Yhteenvetona…

• Joukot ovat erittäin tehokkaita tietorakenteita, jotka tallentavat samantyyppisiä elementtejä. Elementtien tyyppi ja matriisin koko ovat kiinteitä ja ne määritellään matriisia luotaessa.
• Muisti varataan heti matriisin luomisen jälkeen ja se on tyhjä, kunnes annat arvoja.
• Muistissa elementit sijaitsevat vierekkäisissä paikoissa, joten niitä voidaan käyttää erittäin tehokkaasti (satunnaiskäyttö, O(1) = vakioaika) indeksejä käyttäen.
• Indeksit alkavat 0:sta, eivät 1:stä, kuten olemme tottuneet.
• Elementtien lisääminen matriisin alkuun tai keskelle edellyttää elementtien siirtämistä oikealle. Jos array on täynnä, luodaan uusi, suurempi array (mikä ei ole kovin tehokasta). Joukon lopussa lisääminen on erittäin tehokasta, vakioaika O(1).
• Elementtien poistaminen joukon alusta tai keskeltä edellyttää kaikkien elementtien siirtämistä vasemmalle, jotta muistiin ei jäisi tyhjää tilaa. Näin taataan, että elementit tallennetaan muistin vierekkäisiin tiloihin. Poistaminen joukon lopussa on erittäin tehokasta, koska poistat vain viimeisen elementin.
• Löytääksesi elementin, sinun on tarkistettava koko joukko, kunnes löydät sen. Jos tiedot ovat lajiteltuja, voit käyttää algoritmeja, kuten binäärihakua, prosessin optimoimiseksi.

”Opi eilisestä, elä tätä päivää, toivo huomista”. Tärkeintä on, ettet lakkaa kyseenalaistamasta.”
– Albert Einstein

👋 Kiitos!

Toivon todella, että pidit artikkelistani. ❤️
Seuraa minua Twitterissä löytääksesi lisää tämän kaltaisia artikkeleita. 😃