Ryhmä 
on äärellinen tai ääretön joukko alkioita yhdessä binäärioperaation (jota kutsutaan ryhmäoperaatioksi) kanssa, jotka yhdessä täyttävät neljä perusominaisuutta: sulkeutuneisuus, assosiatiivisuus, identiteettiominaisuus ja käänteisominaisuus. Operaatiota, jonka suhteen ryhmä määritellään, kutsutaan usein ”ryhmäoperaatioksi”, ja joukon sanotaan olevan ryhmä ”tämän operaation alla”. Elementit 
, 
, 
, …, joiden välillä 
ja 
on binäärioperaatio 
, muodostavat ryhmän, jos
1. Sulkeuma: Jos 
ja 
ovat kaksi alkiota 
:ssä, niin tuote 
on myös 
:ssä.
2. Assosiatiivisuus: Määritelty kertolasku on assosiatiivinen, eli kaikille 
, 
.
3. Identiteetti: On olemassa identiteettielementti 
(eli 1, 
tai 
) siten, että 
jokaiselle elementille 
.
4. Käänteinen: Jokaiselle alkuaineelle on oltava käänteisluku (eli käänteisluku). Näin ollen jokaiselle 
:n 
alkioille joukko sisältää sellaisen alkion 
, että 
.
Ryhmä on monoidi, jonka jokainen alkioista on käänteismuunnettavissa.
Ryhmässä on oltava vähintään yksi alkio, jolloin ainutkertainen (isomorfismiin asti) yhden alkion ryhmä tunnetaan nimellä triviaaliryhmä.
Ryhmien tutkiminen tunnetaan nimellä ryhmäteoria. Jos elementtejä on äärellinen määrä, ryhmää kutsutaan äärelliseksi ryhmäksi ja elementtien lukumäärää kutsutaan ryhmän ryhmäjärjestykseksi. Ryhmän osajoukkoa, joka on suljettu ryhmäoperaatiolle ja käänteisoperaatiolle, kutsutaan alaryhmäksi. Myös alaryhmät ovat ryhmiä, ja monet yleisesti esiintyvät ryhmät ovat itse asiassa jonkin yleisemmän suuremman ryhmän erityisiä alaryhmiä.
Perusesimerkki äärellisestä ryhmästä on symmetrinen ryhmä 
, joka on 
kohteiden permutaatioiden (tai ”permutaation alla”) ryhmä. Yksinkertaisin ääretön ryhmä on kokonaislukujen joukko tavanomaisen yhteenlaskun alla. Jatkuvien ryhmien osalta voidaan tarkastella reaalilukuja tai 
käänteismatriisien joukkoa. Nämä kaksi viimeksi mainittua ovat esimerkkejä Lie-ryhmistä.
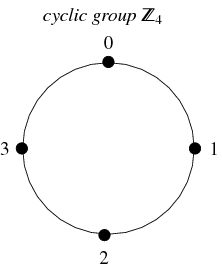
Yksi hyvin yleinen ryhmätyyppi ovat sykliset ryhmät. Tämä ryhmä on isomorfinen kokonaislukujen ryhmälle (modulo 
), sitä merkitään 
, 
tai 
, ja se on määritelty jokaiselle kokonaisluvulle 
. Se on suljettu yhteenlaskun suhteen, assosiatiivinen ja sillä on yksikäsitteiset käänteisluvut. Luvut 0 – 
edustavat sen alkioita, identiteettielementtiä edustaa 0, ja 
:n käänteislukua edustaa 
.
Kahden ryhmän välistä karttaa, joka säilyttää identiteetin ja ryhmäoperaation, kutsutaan homomorfismiksi. Jos homomorfismilla on käänteisluku, joka on myös homomorfismi, sitä kutsutaan isomorfismiksi ja kahta ryhmää kutsutaan isomorfisiksi. Kahta keskenään isomorfista ryhmää pidetään ”samoina”, kun niitä tarkastellaan abstrakteina ryhminä. Esimerkiksi alla olevassa kuvassa esitetty neliön kiertoryhmä on syklinen ryhmä 
.
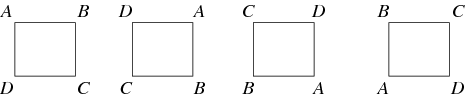
Yleisesti ryhmävuorovaikutuksesta on kyse, kun ryhmä vaikuttaa joukkoon ja permutoi sen alkioita siten, että kartta ryhmästä joukon permutaatioryhmään on homomorfismi. Esimerkiksi neliön rotaatiot ovat sen kulmien permutaatioiden alaryhmä. Minkä tahansa ryhmän 
yksi tärkeä ryhmätoiminto on sen toiminta itseensä konjugaation avulla. Nämä ovat vain joitakin mahdollisia ryhmäautomorfismeja. Toinen tärkeä ryhmävuorovaikutus on ryhmän representaatio, jossa ryhmä vaikuttaa vektoriavaruuteen käänteismuunnettavien lineaarikarttojen avulla. Kun vektoriavaruuden kenttä on kompleksiluvut, edustusta kutsutaan joskus CG-moduuliksi.
Ryhmätoiminnot ja erityisesti edustukset ovat hyvin tärkeitä sovelluksissa paitsi ryhmäteoriassa myös fysiikassa ja kemiassa. Koska ryhmää voidaan ajatella abstraktina matemaattisena objektina, sama ryhmä voi esiintyä eri yhteyksissä. Siksi on hyödyllistä ajatella, että ryhmän representaatio on ryhmän yksi tietty inkarnaatio, jolla voi olla myös muita representaatioita. Ryhmän redusoitumaton esitys on esitys, jolle ei ole olemassa yksikäsitteistä muunnosta, joka muuttaisi esitysmatriisin lohkodiagonaaliseen muotoon. Pelkistämättömillä esityksillä on joukko huomattavia ominaisuuksia, jotka on virallistettu ryhmän ortogonaalisuusteoriassa.