
Pythagoras Samoslainen (n.570-495 BCE)
Biografia – Kuka oli Pythagoras
Joskus väitetään, että olemme puhtaan matematiikan velkaa Pythagorakselle, ja häntä kutsutaan usein ensimmäiseksi ”oikeaksi” matemaatikoksi. Mutta vaikka hänen panoksensa oli selvästi merkittävä, hän on kuitenkin edelleen kiistelty hahmo.
Hän ei itse jättänyt jälkeensä matemaattisia kirjoituksia, ja suuri osa siitä, mitä tiedämme pythagoralaisesta ajattelusta, on peräisin Philoloksen ja muiden myöhempien pythagoralaisten oppineiden kirjoituksista. Itse asiassa ei ole lainkaan selvää, olivatko monet (tai oikeastaan mitkään) hänelle liitetyistä teoreemoista todellisuudessa Pythagoraan henkilökohtaisesti tai hänen seuraajiensa ratkaisemia.
Koulu, jonka hän perusti Crotoniin Etelä-Italiaan noin vuonna 530 eaa., oli varsin omituisen pythagoralaislahkon ytimenä. Vaikka pythagoralainen ajattelu oli pitkälti matematiikan hallitsemaa, se oli myös syvästi mystistä, ja Pythagoras asetti kaikille koulunsa jäsenille näennäisuskonnolliset filosofiansa, tiukan kasvissyönnin, yhteisöllisen elämäntavan, salaiset riitit ja oudot sääntönsä (mukaan lukien oudot ja ilmeisen sattumanvaraiset määräykset siitä, ettei koskaan saa virtsata aurinkoon päin, ettei koskaan saa mennä naimisiin naisen kanssa, joka käyttää kultakoruja, ettei koskaan saa ohittaa kaduilla makaavaa aasintähteä, että ei saa koskaan syödä tai edes koskettaa mustia härkäpavuja jne.
Jäsenet jakautuivat ”mathematikoi” (tai ”oppijoihin”), jotka jatkoivat ja kehittivät Pythagoraan itsensä aloittamaa matemaattisempaa ja tieteellisempää työtä, ja ”akousmatikoi” (tai ”kuuntelijoihin”), jotka keskittyivät Pythagoraan opetusten uskonnollisempiin ja ritualistisempiin puoliin. Näiden kahden ryhmän välillä oli aina jonkin verran kitkaa, ja lopulta lahko ajautui kiivaisiin paikallisiin taisteluihin ja hajaantui lopulta. Pythagoralaisten salamyhkäisyyttä ja yksinoikeutta kohtaan syntyi kaunaa, ja vuonna 460 eaa. kaikki heidän kokoontumispaikkansa poltettiin ja tuhottiin, ja ainakin 50 jäsentä sai surmansa pelkästään Crotonissa.
Pythagoraan koulukunnan tärkein sanonta oli ”Kaikki on numeroa” tai ”Jumala on numero”, ja pythagoralaiset harjoittivat käytännössä eräänlaista numerologiaa tai numeronpalvontaa, ja he katsoivat, että kullakin numerolla oli oma luonteensa ja merkityksensä. Esimerkiksi numero yksi oli kaikkien numeroiden generaattori, kaksi edusti mielipidettä, kolme harmoniaa, neljä oikeudenmukaisuutta, viisi avioliittoa, kuusi luomista, seitsemän seitsemää planeettaa tai ”vaeltavia tähtiä” jne. Parittomia numeroita pidettiin naisellisina ja parillisia numeroita miespuolisina.
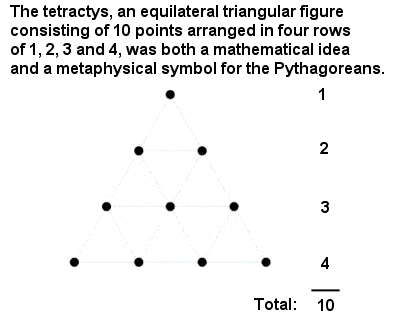
Pythagoralainen Tetraktys
Pyhin kaikista luvuista oli ”Tetraktys” eli kymppi, kolmionmuotoinen luku, joka muodostui ykkösen, kakkosen, kolmosen ja nelosen summasta. On suuri kunnianosoitus pythagoralaisten älyllisille saavutuksille, että he päättelivät luvun 10 erityisaseman abstraktista matemaattisesta väitteestä eivätkä jostain niinkin arkipäiväisestä asiasta kuin kahden käden sormien laskemisesta.
Pythagoras ja hänen koulukuntansa – samoin kuin kourallinen muita muinaisen Kreikan matemaatikkoja – oli kuitenkin suurelta osin vastuussa siitä, että he ottivat käyttöön aikaisempaa tiukemman matematiikan, joka rakentui ensimmäisistä lähtökohdista aksioomien ja logiikan avulla. Ennen Pythagorasta esimerkiksi geometria oli ollut pelkkä kokoelma empiiristen mittausten perusteella johdettuja sääntöjä.
Pythagoras havaitsi, että voitiin rakentaa täydellinen matematiikkajärjestelmä, jossa geometriset elementit vastasivat lukuja ja jossa kokonaisluvut ja niiden suhteet olivat kaikki, mitä tarvittiin kokonaisen logiikka- ja totuusjärjestelmän luomiseen.
Pythagoraan lause
Hänet muistetaan pääasiassa siitä, mikä on tullut tunnetuksi nimellä Pythagoraan lause (tai Pythagoraan lause): että minkä tahansa suorakulmaisen kolmion hypotenuusan (pisimmän sivun, joka on vastapäätä suoraa kulmaa) pituuden neliö on yhtä suuri kuin kahden muun sivun (tai ”jalan”) neliöiden summa.
Yhtälönä kirjoitettuna: a2 + b2 = c2.
Mitä Pythagoras ja hänen seuraajansa eivät ymmärtäneet, on se, että tämä toimii myös minkä tahansa muodon kohdalla: näin ollen hypotenuusan viisikulmion pinta-ala on yhtä suuri kuin kahden muun sivun viisikulmioiden summa, kuten puoliympyrän tai minkä tahansa muun säännöllisen (tai jopa epäsäännöllisen( muodon kohdalla.
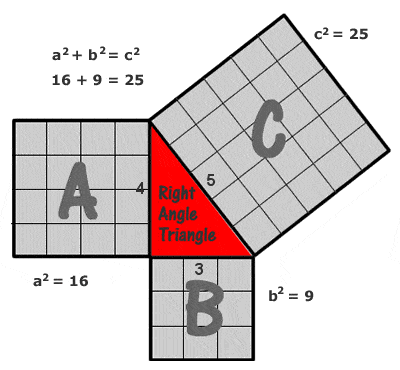
Pythagoraan (Pythagoraan) lause
Yksinkertaisin ja yleisimmin siteerattu esimerkki Pythagoraan kolmiosta on kolmio, jonka sivut ovat 3, 4 ja 5 yksikköä (32 + 42 = 52, kuten voidaan nähdä piirtämällä kumpaankin sivuun yksikköneliöistä koostuva ruudukko, kuten oikealla olevassa kuvassa), mutta on olemassa potentiaalisesti ääretön määrä muita kokonaislukuisia ”Pythagoraan kolmioita”, alkaen (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41) jne. On kuitenkin huomattava, että (6, 8, 10) ei ole niin sanottu ”primitiivinen” Pythagoraan kolmio, koska se on vain (3, 4, 5):n kerrannainen.
Pythagoraan lause ja suorakulmaisten kolmioiden ominaisuudet näyttävät olevan aritmetiikan ja geometrian peruslaskutoimitusten jälkeen muinaisinta ja laajimmalle levinnyttä matemaattista kehitystyötä, ja sitä käsiteltiin joissakin muinaisimmissa matemaattisissa teksteissä Babyloniassa ja Egyptissä, jotka ovat yli tuhat vuotta varhaisemmalta ajalta. Yksi yksinkertaisimmista todistuksista on peräisin muinaisesta Kiinasta, ja se on luultavasti peräisin paljon ennen Pythagoraan syntymää. Pythagoras oli kuitenkin se, joka antoi teoreemalle sen lopullisen muodon, vaikka ei olekaan selvää, todistiko Pythagoras itse sen lopullisesti vai pelkästään kuvailiko hän sitä. Joka tapauksessa siitä on tullut yksi tunnetuimmista matemaattisista lauseista, ja nykyään on olemassa jopa 400 erilaista todistusta, joista osa on geometrisia, osa algebrallisia, osa sisältää kehittyneitä differentiaaliyhtälöitä jne.
Pian kävi kuitenkin ilmi, että myös muut kuin kokonaislukuja sisältävät ratkaisut olivat mahdollisia, joten esimerkiksi tasakylkisellä kolmiolla, jonka sivuilla on sivut 1, 1 ja √2, on myös suorakulmainen kulma, kuten babylonialaiset olivat havainneet vuosisatoja aiemmin. Kun Pythagoraan oppilas Hippasos yritti kuitenkin laskea √2:n arvon, hän huomasi, ettei sitä ollut mahdollista ilmaista murtolukuna, mikä osoitti, että oli olemassa kokonaan uusi lukujen maailma, irrationaaliluvut (luvut, joita ei voida ilmaista kokonaislukujen yksinkertaisina murtolukuina). Tämä löytö melkoisesti murskasi Pythagoraan ja hänen seuraajiensa rakentaman tyylikkään matemaattisen maailman, ja sellaisen luvun olemassaolo, jota ei voitu ilmaista kahden Jumalan luomuksen suhdelukuna (kuten he ajattelivat kokonaisluvuista), vaaransi koko kultin uskomusjärjestelmän.
Salaisuudenhaluiset pythagoralaiset hukuttivat Hippasos-paran ilmeisesti sen vuoksi, että hän oli levittänyt tämän tärkeän löydön ulkomaailmaan. Mutta kokonaislukujen jumalallisuuden ajatuksen korvaaminen rikkaammalla jatkumon käsitteellä oli olennainen kehitysaskel matematiikassa. Se merkitsi kreikkalaisen geometrian todellista syntyä, sillä geometria käsittelee viivoja, tasoja ja kulmia, jotka kaikki ovat jatkuvia eivätkä erillisiä.
Muiden geometristen saavutustensa ohella Pythagoras (tai ainakin hänen seuraajansa, pythagoralaiset) oivalsi myös sen, että kolmion kulmien summa on yhtä suuri kuin kaksi suoraa kulmaa (180°), ja luultavasti myös sen yleistyksen, jonka mukaan n-sivuisen monikulmion sisäkulmien summa on yhtä suuri kuin (2n – 4) suoraa kulmaa ja että sen ulkokulmien summa on yhtä suuri kuin neljä suoraa kulmaa. He pystyivät rakentamaan tietyn pinta-alan omaavia kuvioita ja käyttämään yksinkertaista geometrista algebraa, esimerkiksi ratkaisemaan yhtälöitä, kuten a(a – x) = x2, geometrisin keinoin.
Pythagoralaiset loivat myös lukuopin perustan tutkimalla kolmi- ja neliölukuja sekä täydellisiä lukuja (lukuja, jotka ovat jakajiensa summa). He löysivät useita uusia neliölukujen ominaisuuksia, kuten sen, että luvun n neliö on yhtä suuri kuin n ensimmäisen parittoman luvun summa (esim. 42 = 16 = 1 + 3 + 5 + 7). He löysivät myös ainakin ensimmäisen sopusointuisten lukujen parin, 220 ja 284 (sopusointuiset luvut ovat lukupareja, joissa toisen luvun jakajien summa on yhtä suuri kuin toisen luvun summa, esim. 220:n sopusointuiset jakajat ovat 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 ja 110, joiden summa on 284; ja 284:n sopusointuiset jakajat ovat 1, 2, 4, 71 ja 142, joiden summa on 220).
Musiikin teoria
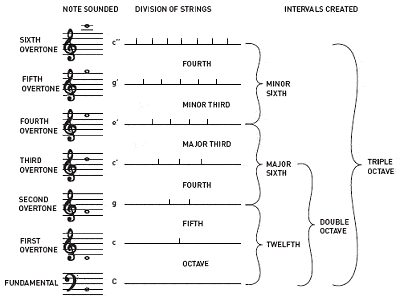
Pythagoraan katsotaan löytäneen sopusointuisten sävelten väliset suhteet
Pythagoraan katsotaan myös löytäneen, että sopusointuisten sävelten välisillä väleillä on aina kokonaislukujen suhteet. Esimerkiksi kitarajousen puolen pituuden soittaminen antaa saman sävelen kuin avoin jousi, mutta oktaavia korkeammalla; kolmasosa pituudesta antaa erilaisen, mutta harmonisen sävelen jne.
Ei-kokonaislukusuhteet sen sijaan antavat yleensä dissonoivia ääniä. Näin Pythagoras kuvasi neljä ensimmäistä yläsointua, jotka luovat yhteisiä intervalleja, joista on tullut musiikillisen harmonian ensisijaisia rakennuspalikoita: oktaavi (1:1), täydellinen viidesosa (3:2), täydellinen neljäsosa (4:3) ja suuri kolmasosa (5:4). Vanhin tapa virittää 12-sävelinen kromaattinen asteikko tunnetaan nimellä pythagoralainen viritys, ja se perustuu täydellisten kvinttien pinoon, joista kukin on viritetty suhteessa 3:2.
Mystinen Pythagoras innostui tästä löydöstä niin paljon, että hän vakuuttui siitä, että koko maailmankaikkeus perustui numeroihin ja että planeetat ja tähdet liikkuivat matemaattisten yhtälöiden mukaan, jotka vastasivat musiikkisäveliä, ja tuotti näin eräänlaisen sinfonian, ”Musical Universalis” eli ”sfääreiden musiikin”.
| << Takaisin kreikkalaiseen matematiikkaan | Eteenpäin Platoniin >> |
