Tässä osiossa perehdymme joukko-operaatioihin ja merkintöihin, jotta voimme soveltaa näitä käsitteitä sekä laskenta- että todennäköisyysongelmiin. Aloitamme määrittelemällä joitakin termejä.
joukko on kokoelma objekteja, ja sen jäseniä kutsutaan joukon alkioiksi. Nimeämme joukon käyttämällä isoja kirjaimia ja suljemme sen jäsenet sulkeisiin. Oletetaan, että haluamme luetella shakkikerhon jäsenet. Käytämme seuraavaa joukon merkintätapaa.
C ={Ken, Bob, Tran, Shanti, Eric}
joukkoa, jolla ei ole jäseniä, kutsutaan tyhjäksi joukoksi. Tyhjää joukkoa merkitään symbolilla Ø.
Kaksi joukkoa on yhtäläisiä, jos niillä on samat alkiot.
joukko A on joukon B osajoukko, jos jokainen A:n jäsen on myös B:n jäsen.
Esitellään, että C = {Al, Bob, Chris, David, Ed} ja A = {Bob, David}. Tällöin A on C:n osajoukko, joka kirjoitetaan 
.
Jokainen joukko on itsensä osajoukko, ja tyhjä joukko on jokaisen joukon osajoukko.
Kahden joukon unioni
Asettakaamme A:n ja B:n olevan kaksi joukkoa, tällöin A:n ja B:n unioni, joka kirjoitetaan 
, on kaikkien niiden alkioiden joukko, jotka ovat joko A:ssa tai B:ssä, tai sekä A:ssa että B:ssä.
Kahden joukon leikkaus
Jos A ja B ovat kaksi joukkoa, niin A:n ja B:n leikkaus, kirjoitettuna 
, on kaikkien niiden alkioiden joukko, jotka ovat yhteisiä molemmille joukoille A ja B.
Yleisjoukko U on kaikkien tarkasteltavien alkioiden muodostama joukko.
joukon komplementti
Jos A on mikä tahansa joukko, niin joukon A komplementti, kirjoitettuna 
, on joukko, joka koostuu universaalin joukon U alkioista, jotka eivät ole joukossa A.
Epäyhtenäiset joukot
Kahta joukkoa A ja B sanotaan epäyhtenäisiksi joukoiksi, jos niiden leikkauspiste on tyhjä joukko.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {oranssi, vihreä, indigo, violetti} Paremman ymmärryksen saavuttamiseksi olettakaamme, että universaali joukko U edustaa spektrin värejä ja P perusvärejä, jolloin edustaa niitä spektrin värejä, jotka eivät ole perusvärejä.
.
= {punainen, keltainen, sininen, vihreä}
= {oranssi, indigo, violetti}
= {punainen, keltainen, sininen, violetti} = {violetti}Venn-diagrammit
Käytämme nyt Venn-diagrammeja havainnollistamaan joukkojen välisiä suhteita. Englantilainen loogikko John Venn kehitti 1800-luvun lopulla menetelmän joukkojen välisten suhteiden esittämiseksi. Hän esitti nämä suhteet kaavioilla, jotka tunnetaan nykyään Venn-diagrammeina. Venn-diagrammi esittää joukon ympyrän sisäpuolena. Usein kaksi tai useampi ympyrä on suljettu suorakulmion sisään, jossa suorakulmio edustaa yleisjoukkoa. Joukon leikkauksen tai liiton visualisointi on helppoa. Tässä luvussa käytämme Venn-diagrammeja lähinnä erilaisten joukkojen lajitteluun ja kohteiden laskemiseen.
|
(a) |
(b) |
(c) |
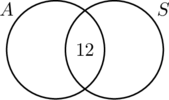
Koska 30 ihmistä ajoi automaattivaihteisilla autoilla, ympyrän A täytyy sisältää 30 elementtiä. Tämä tarkoittaa, että x + 12 = 30 tai x = 18. Vastaavasti, koska 20 ihmistä ajoi autoja, joissa on vakiovaihteisto, ympyrän B on sisällettävä 20 elementtiä eli y +12 = 20, mikä puolestaan tekee y = 8.
Nyt kun kaikki tiedot on järjestetty, kaaviosta on helppo lukea, että 18 ihmistä ajoi autoja, joissa on vain automaattivaihteisto, 12 ihmistä ajoi molempia autotyyppejä ja 8 ihmistä ajoi autoja, joissa on vain vakiovaihteisto. Kyselyyn osallistui siis 18 + 12 + 8 = 38 ihmistä.
|
(a) |
(b) |
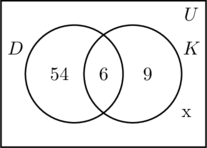
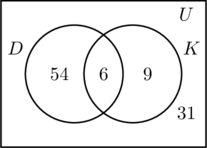
Täytämme joukkoihin D ja K liittyvät kolme aluetta samalla tavalla kuin aiemmin. Koska kyselyyn osallistui 100 ihmistä, universaalia joukkoa U kuvaavan suorakulmion on sisällettävä 100 kohdetta. Olkoon x niitä universaalijoukon henkilöitä, jotka eivät kuulu joukkoon D eivätkä joukkoon K. Tämä tarkoittaa, että 54 + 6 + 9 + x = 100 eli x = 31.
Selvityksessä on siis 31 henkilöä, jotka eivät ole käyneet kummassakaan paikassa.
- 50 hölkkäävät, 30 uivat ja 35 pyöräilevät
- 14 hölkkäävät ja uivat
- 7 uivat ja pyöräilevät
- 9 hölkkäävät ja pyöräilevät
- 3 henkilöä harrastaa kaikkia kolmea liikuntamuotoa
Ratkaisu
|
(a) |
(b) |
(c) |
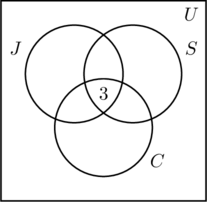
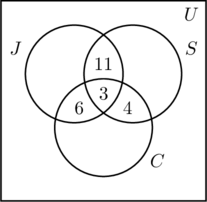
Sijoitamme 3:n kuvion (a) sisimpään alueeseen, koska se edustaa niiden ihmisten määrää, jotka osallistuvat kaikkiin kolmeen toimintaan. Seuraavaksi lasketaan x, y ja z.
- Koska 14 ihmistä hölkkää ja ui, x +3 = 14 eli x = 11.
- Koska 9 ihmistä hölkkää ja pyöräilee, saadaan y + 3 = 9 eli y = 6.
- Koska 7 ihmistä ui ja pyöräilee, z + 3 = 7 eli z = 4.
- Tämä tieto on esitetty kuvassa (b).
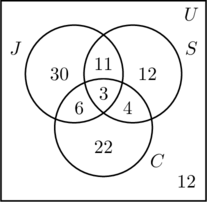
- Koska 50 ihmistä hölkkää, m + 11 + 6 + 3 = 50 eli m = 30.
- 30 ihmistä ui, joten n + 11 + 4 + 3 = 30 eli n = 12.
- 35 ihmistä pyöräilee, joten p + 6 + 4 + 3 = 35 eli p = 22.
- Lisäämällä kaikkien kolmen joukon merkinnät yhteen saadaan summaksi 88. Koska 100 ihmistä tutkittiin, universaalin joukon sisällä, mutta kaikkien kolmen joukon ulkopuolella oleva määrä on 100 – 88 eli 12.
- Kuvassa (c) tiedot ovat järjestyksessä, ja kysymyksiin voidaan helposti vastata.
Harjoituskysymykset
1. Olkoon universaali joukko U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h} ja W = {a, c, e, g, i}. Luettele seuraavien joukkojen jäsenet:
a. 
b. 
2. Tarkastellaan seuraavia joukkoja: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, influenssa, Norovirus}, B = {Listeria, kampylobakteeri, salmonella, E. coli O157, Norovirus, Shigella} ja C = {SARS, Listeria, tuberkuloosi, H5N1, salmonella, HIV, COVID-19}. Luettele seuraavien joukkojen jäsenet:
a. 
b. 
3. Urheilijoille tehty kyselytutkimus osoitti, että pieniin särkyihin ja kipuihin 30 käytti aspiriinia, 50 ibuprofeenia ja 15 käytti molempia. Kaikki kyselyyn osallistuneet urheilijat käyttivät ainakin yhtä näistä kahdesta särkylääkkeestä. Kuinka monta urheilijaa tutkittiin?
4. 150 lukiolaiselle tehdyssä tutkimuksessa havaittiin, että 25 ilmoitti, että heillä oli ollut aiempi aivotärähdys tai päävamma, 52 ilmoitti kokeneensa mielenterveysongelmia ja 15 ilmoitti molemmista tuloksista. Kuinka moni opiskelija ei ilmoittanut kumpaakaan tulosta?
5. Ryersonin yliopiston 100 opiskelijalle tehdyssä kyselyssä todetaan, että 50 tilaa Netflixin, 40 tilaa Amazon Primen ja 30 tilaa Disney+:n. Näistä 15 tilaa sekä Netflixin että Amazon Primen, 10 sekä Amazon Primen että Disney+:n, 10 sekä Netflixin että Disney+:n ja viidellä on kaikki kolme tilauspalvelua. Piirrä Venn-diagrammi ja määritä seuraavat:
a. Niiden opiskelijoiden määrä, jotka tilaavat Amazon Primen mutta eivät kahta muuta suoratoistopalvelua.
b. Niiden opiskelijoiden määrä, jotka tilaavat Netflixin tai Amazon Primen mutta eivät Disney+:n.
c. Niiden opiskelijoiden määrä, jotka eivät tilaa mitään näistä palveluista.