Veden faasidiagrammi
Kuvassa 11.23 ”Kaksi versiota veden faasidiagrammista” on esitetty veden faasidiagrammi ja havainnollistetaan, että veden kolmoispiste on 0,01 °C:n lämpötilassa ja 0,00604 atm:ssa (4,59 mmHg). Kolmiopistettä (273,16 K) käytetään absoluuttisen (kelvinin) lämpötila-asteikon määrittelyssä, koska se on paljon toistettavampi kuin jään sulamispiste, joka riippuu liuenneen ilman määrästä ja ilmanpaineesta. Kolmoispiste edustaa myös alinta painetta, jossa nestefaasi voi olla tasapainossa kiinteän aineen tai höyryn kanssa. Alle 0,00604 atm:n paineessa jää ei siis sula nesteeksi lämpötilan noustessa, vaan kiinteä aine sublimoituu suoraan vesihöyryksi. Veden sublimoitumista alhaisessa lämpötilassa ja paineessa voidaan käyttää elintarvikkeiden ja juomien ”pakkaskuivaamiseen”. Elintarvike tai juoma jäähdytetään ensin pakkaslämpötilaan ja asetetaan astiaan, jossa paine pidetään alle 0,00604 atm. Sitten, kun lämpötilaa nostetaan, vesi sublimoituu, jolloin jäljelle jää dehydratoitu ruoka (kuten reppumatkailijoiden tai astronauttien käyttämä ruoka) tai jauhemainen juoma (kuten pakastekuivattu kahvi).
Veden faasidiagrammi, joka on esitetty osassa (b) kuvassa 11.23 ”Veden faasidiagrammin kaksi versiota”, näyttää jään ja veden välisen rajan laajennetussa mittakaavassa. Jään sulamiskäyrä viettää ylöspäin ja hieman vasemmalle eikä ylöspäin ja oikealle kuten kuvassa 11.22 ”Tyypillinen faasidiagrammi aineelle, jolla on kolme faasia – kiinteä, neste ja kaasu – ja ylikriittinen alue”; eli jään sulamispiste laskee paineen kasvaessa; 100 MPa:n (987 atm) paineessa jää sulaa -9 °C:ssa. Vesi käyttäytyy näin, koska se on yksi harvoista tunnetuista aineista, joiden kiteinen kiinteä aine on vähemmän tiheä kuin neste (muita ovat antimoni ja vismutti). Jään, joka on tasapainossa veden kanssa 0 °C:ssa ja 1 atm:n lämpötilassa, paineen nostaminen työntää osan molekyyleistä lähemmäs toisiaan, jolloin näytteen tilavuus pienenee. Tilavuuden pieneneminen (ja vastaava tiheyden kasvu) on pienempi kiinteällä tai nestemäisellä aineella kuin kaasulla, mutta se riittää sulattamaan osan jäästä.
Kuva 11.23 Kaksi versiota veden faasidiagrammista
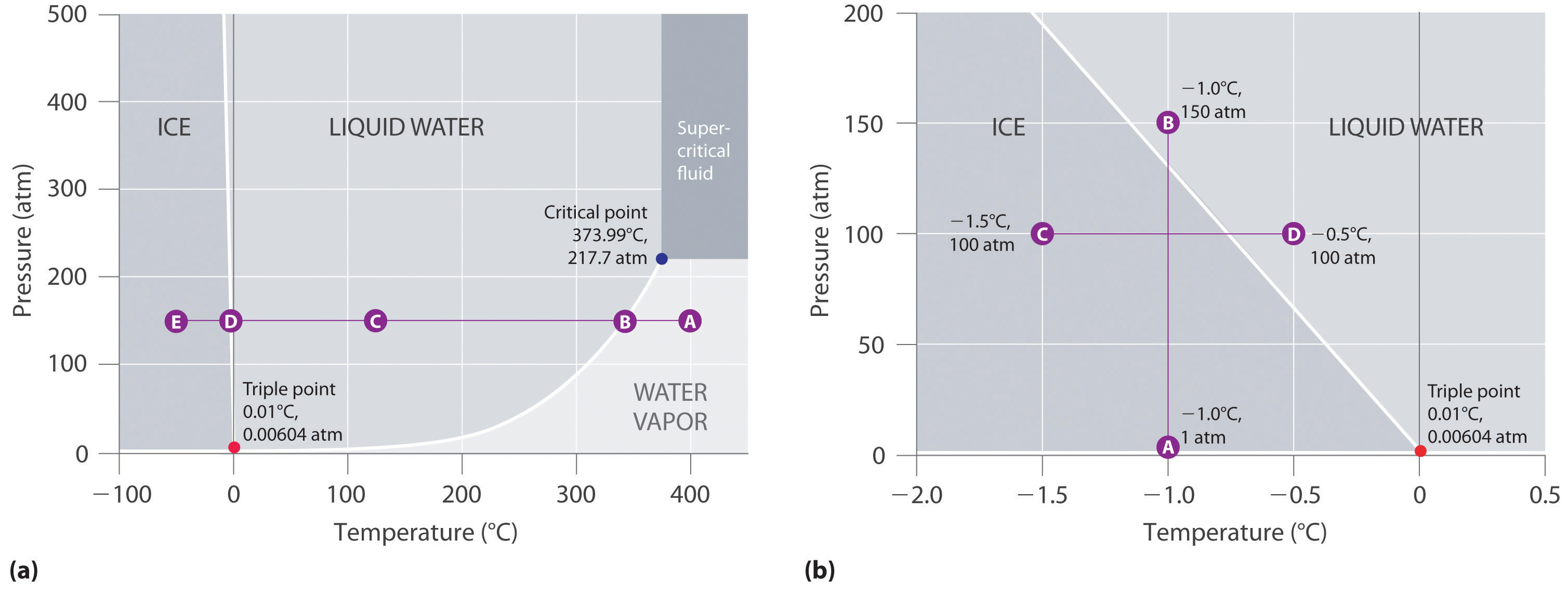
(a) Tässä kuvaajassa, jossa on lineaariset lämpötilaa ja painetta kuvaavat akselit, jään ja nestemäisen veden raja kulkee lähes pystysuorassa. (b) Tämä kuvaaja, jossa on laajennettu asteikko, havainnollistaa sulamispisteen laskua paineen kasvaessa. (Kirjaimet viittaavat esimerkissä 10 käsiteltyihin pisteisiin.)
Kuvan 11.23 ”Veden faasidiagrammin kaksi versiota” osassa (b) piste A sijaitsee lämpötilassa P = 1 atm ja T = -1,0 °C, faasidiagrammin kiinteällä (jää) alueella. Kun paine kasvaa 150 atm:iin lämpötilan pysyessä samana, pisteestä A lähtevä viiva ylittää jään ja veden rajan pisteeseen B, joka sijaitsee nestemäisen veden alueella. Näin ollen 150 atm:n paine sulattaa jään -1,0 °C:n lämpötilassa. Olemme jo osoittaneet, että veden sulamispisteen riippuvuus paineesta on erittäin tärkeää. Jos veden faasidiagrammissa kiinteän ja nestemäisen välinen raja kulkisi ylöspäin ja oikealle eikä vasemmalle, jää olisi vettä tiheämpää, jääkuutiot uppoaisivat, vesiputket eivät puhkeaisi jäätyessään ja pakkasnestettä ei tarvitsisi käyttää autojen moottoreissa.
Vielä viime aikoihin asti monissa oppikirjoissa kuvailtiin luistelua mahdolliseksi siksi, että luistelijan terän aiheuttama paine on tarpeeksi suuri sulattaakseen jään jään terän alla ja luodakseen siten nestemäisen veden voitelukerroksen, jonka avulla terä voi liukua jään pinnalla. Vaikka tämä selitys on intuitiivisesti tyydyttävä, se on virheellinen, kuten voimme osoittaa yksinkertaisella laskutoimituksella. Muistetaan luvusta 10 ”Kaasut”, että paine (P) on pinta-alayksikköä (A) kohti kohdistuva voima (F):
Yhtälö 11.4
P = F A
Lasketakseen luistelijan jäähän kohdistaman paineen, meidän on laskettava vain kohdistuva voima ja luistimen terän pinta-ala. Jos oletetaan, että luistelija painaa 75,0 kg (165 lb), niin luistelijan jäähän kohdistama painovoiman aiheuttama voima on
Yhtälö 11.5
F = mg
jossa m on massa ja g on Maan painovoiman aiheuttama kiihtyvyys (9,81 m/s2). Voima on siis
Yhtälö 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Jos oletetaan, että luistimen terät ovat 2 kpl.0 mm leveät ja 25 cm pitkät, niin kunkin terän pohjan pinta-ala on
Yhtälö 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Jos luistelija liukuu yhdellä jalalla, jäähän kohdistuva paine on
Yhtälö 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Paine on paljon pienempi kuin paine, joka tarvitaan jään sulamispisteen alentamiseen edes 1 °C:lla, ja kokemuksen mukaan luistelu on mahdollista myös silloin, kun lämpötila on selvästi pakkasen alapuolella. Näin ollen paineen aiheuttama jään sulaminen ei voi selittää pientä kitkaa, joka mahdollistaa luistelijoiden (ja jääkiekkokiekkojen) liukumisen. Viimeaikaiset tutkimukset osoittavat, että jään pinta, jossa vesimolekyylien järjestäytynyt joukko kohtaa ilman, koostuu yhdestä tai useammasta lähes nestemäisen veden kerroksesta. Nämä kerrokset yhdessä kitkan aiheuttaman sulamisen kanssa luistelijan työntyessä eteenpäin näyttävät selittävän sekä luistelijan liukumisen helppouden että sen, että luistelu vaikeutuu noin -7 °C:n lämpötilan alapuolella, kun voitelevien vesikerrosten määrä vähenee.
