Tiede > Fysiikka > Valosähköinen ilmiö >Einsteinin valosähköinen yhtälö
Tässä artikkelissa johdetaan Einsteinin valosähköinen yhtälö ja tutkitaan sen käyttöä valon valosähköisen ilmiön ominaisuuksien todentamiseksi.
Valon aaltoluonne:
Christian Huygen ehdotti, että valo etenee aallon muodossa. Tällä teorialla on kuitenkin vakava haittapuoli. Se ei pystynyt selittämään valon etenemistä tyhjiössä. Tämän epäkohdan poisti Maxwell, joka ehdotti, että valo on sähkömagneettinen aalto ja että sähkömagneettisten aaltojen etenemiseen ei tarvita aineellista väliaineita. Näin vahvistettiin valon aaltoluonne.
Aaltoteoria pystyi selittämään kaikki valon etenemiseen liittyvät ilmiöt. Se ei kuitenkaan kyennyt selittämään energian jakautumista eikä nykyaikaisia ilmiöitä, kuten valosähköistä vaikutusta, Cromptonin vaikutusta jne.
Valon hiukkasluonne:
Max Planck osoitti, että valon tai energian eteneminen tapahtuu energiapaketteina, joita kutsutaan kvanteiksi. Valon kvanttia kutsutaan fotoniksi, ja näin hän vahvisti valon hiukkasluonteen. Käyttämällä säteilyn hiukkas- tai kvanttiluonnetta voimme selittää valosähköisen ilmiön ja Cromptonin ilmiön.
Planckin kvanttiteoria:
Kvanttiteoriaa ehdotti Max Planck. Tämän teorian mukaan säteilyä ei lähde jatkuvasti, vaan se säteilee energiapaketteina tai -nippuina. Näitä paketteja kutsutaan kvanteiksi tai fotoneiksi. Jos säteilyn taajuus on ν, jokaisella kvantilla on energiaa, jossa h on Planckin vakio.
Siten fotonin energia = E = hν
Energia säteilee epäjatkuvasti. Tämä on vastoin klassista teoriaa, jossa oletetaan, että energian emissio on jatkuva prosessi.
Sähkömagneettisen säteilyn hiukkasluonne:
Säteilyn ja aineen vuorovaikutuksessa säteily käyttäytyy ikään kuin se koostuisi hiukkasista. Näitä hiukkasia kutsutaan fotoneiksi. Kullakin fotonilla on energiaa, joka annetaan
E = hν = hc/λ
Kaikkiin tietyn taajuuden (aallonpituuden) omaaviin valofotoneihin liittyy sama energiamäärä. Valon voimakkuuden lisääntyminen lisää tietyn alueen läpi kulkevien fotonien määrää sekunnissa, mutta jokaisen fotonin energia on sama. Fotonit ovat sähköisesti neutraaleja, eivätkä sähkö- tai magneettikentät vaikuta niihin. Fotonit kulkevat suoraviivaisesti valon nopeudella c, mutta tietyissä olosuhteissa niissä esiintyy diffraktiota.
Kunkin fotonin impulssi on
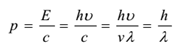
Fotonin aallonpituus muuttuu väliaineen mukaan, joten niillä on erilaiset nopeudet eri väliaineissa. Fotonin lepomassa on nolla. Sen kineettinen massa saadaan
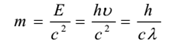
Fotonihiukkasen törmäyksessä (kuten fotonin ja elektronin törmäyksessä) kokonaisenergia ja -impulssi säilyvät. Fotonien lukumäärä ei kuitenkaan välttämättä säily törmäyksessä. Fotoni voi absorboitua tai uusi fotoni voi syntyä.
Einsteinin valosähköinen yhtälö:
Planckin kvanttiteorian pohjalta Einstein johti valosähköisen vaikutuksen yhtälön, joka tunnetaan Einsteinin valosähköisenä yhtälönä. Einstein oletti, että
- Valo koostuu fotoneista eli energiakvanteista, jokaisen fotonin energia on hν. Jossa h on Planckin vakio ja ν on valon taajuus
- Jokainen osuva fotoni törmää atomin sisällä olevaan elektroniin ja luovuttaa kaiken energiansa elektronille.
- Tämän energiasta elektroni käyttää osan tullakseen ulos metallin pinnasta ja loput on kineettistä energiaa, jolla elektroni emittoituu.
- Elektronin tarvitsemaa pienintä energiaa, jonka elektroni tarvitsee tullakseen ulos metallin pinnasta, kutsutaan metallin valosähköiseksi työfunktioksi (∅o).
- Jäljelle jäävä energia (hν – ∅o) on elektronin maksimaalinen liike-energia, jolla fotoelektroni syöksyy ulos.
Elektronin maksimaalinen liike-energia = fotonin energia – työfunktio
Olkoon ’m’ elektronin massa ja vmax fotonielektronin maksimaalinen nopeus, jolla fotonielektroni syöksyy ulos.

Tämä yhtälö tunnetaan Einsteinin valosähköisenä yhtälönä
Fotosähköinen työfunktio:
Fotosähköisessä efektissä valoherkän aineen atomista irtoaa löysimmin kiinnittynyt elektroni. Pienintä energiaa, joka tarvitaan elektronin irrottamiseen tietystä pinnasta, kutsutaan pinnan materiaalin valosähköiseksi työfunktioksi (∅o). Työfunktio on metallipinnalle ominainen ominaisuus.
Matemaattisesti työfunktio saadaan
∅o = h νo
Jossa νo = kynnystaajuus ja h =Planckin vakio.
Kynnystaajuuden olemassaolon selitys Einsteinin valosähköisen yhtälön perusteella:
Tietyllämetallipinnalla fotoelektronit emittoituvat vain silloin, kun osuvan valon taajuus on suurempi tai yhtä suuri kuin tietty minimitaajuus (no)joka tunnetaan kynnystaajuutena. Kynnystaajuus on erilainen eri aineissa,
Einsteinin valosähköisen yhtälön

Jossa νo = kynnystaajuusja h = Planckin vakio ja
ν = osuvan säteilyn taajuus
Kineettinen energia on aina ei-negatiivinen suure i.eli se voi olla joko positiivinen tai nolla, joten

mikä osoittaa, että valosähköisen vaikutuksen aikaansaamiseksi osuvan säteilyn tai osuvan fotonin taajuuden on oltava yhtä suuri tai suurempi kuin kynnystaajuus. Todennäköisiin fotoelektroneihin eri atomeissa vaikuttava vetovoima on erilainen. Siksi kynnystaajuus on erilainen eri aineissa.
Intensiteetin vaikutuksen selittäminenEinsteinin valosähköisen yhtälön perusteella:
Jos osuvan valon taajuus on pienempi kuin kynnystaajuus,fotoelektronit eivät emittoitu, vaikka osuvan valon intensiteetti olisikin kuinka suuri tahansa.
Sekunnissa emittoituvien fotoelektronien määrä on suoraan verrannollinen osuvan valon intensiteettiin. Siten valosähköinen virta on suoraan verrannollinen osuvan valon voimakkuuteen. Jos valon intensiteetti on suurempi, pintaan osuvien fotonien määrä on suurempi. Koska fotoelektronien määrä lisääntyy, fotoemissiovauhti kasvaa, jolloin valosähköisen virran voimakkuus kasvaa. Näin ollen voidaan päätellä, että fotoelektrivaikutus (virta) on suoraan verrannollinen osuvan säteilyn voimakkuuteen.
Mahdollisen maksimaalisen kineettisen energian selitys Einsteinin valosähköisen yhtälön perusteella:
Einsteinin valosähköisen yhtälön

Jossa νo = kynnystaajuusja h = Planckin vakio ja
ν = osuvan säteilyn taajuus
Tämä yhtälö ei sisällä intensiteettitermiä, Näin ollen voidaan sanoa, että fotoelektronin maksimaalinen liike-energia on riippumaton osuvan säteilyn intensiteetistä, mutta riippuu osuvan säteilyn taajuudesta. Yhtälö osoittaa, että elektronin suurin liike-energia riippuu osuvan säteilyn taajuudesta. Ja jos osuvan säteilyn taajuus kasvaa, myös fotoelektronin liike-energia kasvaa.
Valosähköisen vaikutuksen hetkellisyyden selitys Einsteinin valosähköisen yhtälön perusteella:
Valosähköinen vaikutus on hetkellinen prosessi. Valon osumisen ja fotoelektronien emittoitumisen välillä ei ole viiveaikaa, toisin sanoen pinta alkaa emittoida fotoelektroneita heti, kun valo osuu siihen. Myös fotoelektronien emissio loppuu sillä hetkellä, kun osuva valo katkeaa.
Kun säteily osuu valoa emittoivaan pintaan sillä hetkellä, koko fotonin energia siirtyy kerralla yhteen elektroniin. Näin elektroni emittoituu ilman aikaviivettä ja valosähköinen ilmiö on hetkellinen prosessi.
Edellinen aihe:
Seuraava aihe: Numeerisia ongelmia valosähköisestä yhtälöstä
