Accelerație constantă
Analiza mișcării bidimensionale a proiectilului se face prin împărțirea acesteia în două mișcări: pe axa orizontală și pe axa verticală.
Obiective de învățare
Analizați o mișcare bidimensională a unui proiectil de-a lungul axelor orizontală și verticală
Key Takeaways
Key Points
- Accelerația constantă în mișcarea în două dimensiuni urmează, în general, un model de proiectil.
- Mișcarea proiectilului este mișcarea unui obiect aruncat sau proiectat în aer, supus doar accelerației (verticale) datorate gravitației.
- Analizăm mișcarea bidimensională a proiectilului prin descompunerea ei în două mișcări unidimensionale independente de-a lungul axei verticale și orizontale.
Termeni cheie
- cinematic: care are legătură cu mișcarea sau cu cinematica
Mișcarea proiectilului este mișcarea unui obiect aruncat sau proiectat în aer, supus doar forței gravitaționale. Obiectul se numește proiectil, iar traiectoria sa se numește traiectorie. Mișcarea obiectelor în cădere este un tip unidimensional simplu de mișcare a proiectilelor, în care nu există mișcare orizontală. În mișcarea bidimensională a proiectilelor, cum ar fi cea a unei mingi de fotbal sau a unui alt obiect aruncat, există atât o componentă verticală, cât și una orizontală a mișcării.
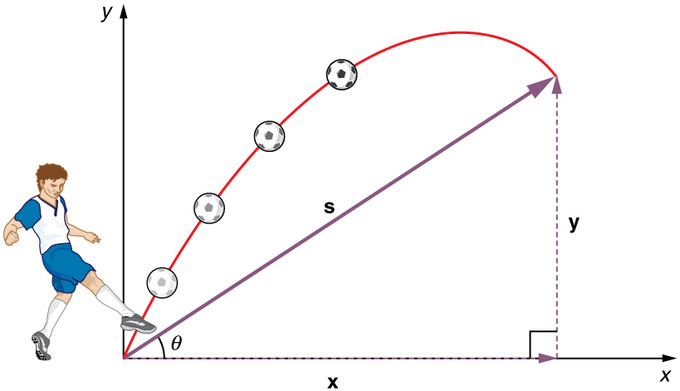
Mișcarea proiectilelor: Aruncarea unei pietre sau lovirea unei mingi produce, în general, un model de mișcare de proiectil care are atât o componentă verticală, cât și una orizontală.
Cel mai important fapt de reținut este că mișcarea de-a lungul axelor perpendiculare este independentă și, prin urmare, poate fi analizată separat. Cheia pentru a analiza mișcarea bidimensională a proiectilului este de a o împărți în două mișcări, una de-a lungul axei orizontale și cealaltă de-a lungul axei verticale. Pentru a descrie mișcarea trebuie să ne ocupăm de viteză și accelerație, precum și de deplasare.
Vom presupune că toate forțele, cu excepția gravitației (cum ar fi rezistența aerului și frecarea, de exemplu), sunt neglijabile. Componentele accelerației sunt atunci foarte simple: \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (presupunem că mișcarea are loc la înălțimi suficient de mici în apropierea suprafeței Pământului astfel încât accelerația datorată gravitației să fie constantă). Deoarece accelerația datorată gravitației are loc numai pe direcția verticală, \text{a}_\text{x} = 0. Astfel, se pot folosi ecuațiile cinematice care descriu mișcarea pe direcțiile \text{x} și respectiv \text{y}:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Analizăm mișcarea bidimensională a proiectilului prin descompunerea ei în două mișcări unidimensionale independente de-a lungul axei verticale și orizontale. Mișcarea orizontală este simplă, deoarece \text{a}_\text{x} = 0 și \text{v}_\text{x} este deci constantă. Viteza pe direcție verticală începe să scadă pe măsură ce un obiect se ridică; în punctul său cel mai înalt, viteza verticală este zero. Pe măsură ce un obiect cade din nou spre Pământ, viteza verticală crește din nou în mărime, dar se îndreaptă în direcția opusă vitezei verticale inițiale. Mișcările \text{x} și \text{y} pot fi recombinate pentru a obține viteza totală în orice punct dat al traiectoriei.
