a.k.a. inter-rater reliability lub concordance
W statystyce, wiarygodność między recenzentami, porozumienie między recenzentami lub concordance jest stopniem zgodności między recenzentami. Daje ona wynik określający, jak bardzo jednorodna lub zgodna jest ocena wystawiona przez sędziów.
Objęte tutaj metody Kappas są najbardziej odpowiednie dla danych „nominalnych”. Naturalne uporządkowanie w danych (jeśli takie istnieje) jest ignorowane przez te metody. Jeśli masz zamiar użyć tych metryk, upewnij się, że jesteś świadomy ograniczeń.
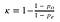
Są dwie części do tego:
- Oblicz obserwowaną zgodność
- Oblicz zgodę przez przypadek
Powiedzmy, że mamy do czynienia z odpowiedziami „tak” i „nie” oraz 2 oceniającymi. Oto oceny:
rater1 =
rater2 =
Przekształcenie tych ocen w macierz dezorientacji:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
Ponieważ zaobserwowana zgodność jest większa niż zgodność przypadkowa, otrzymamy dodatnią Kappa.
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
Albo po prostu użyj implementacji sklearn
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
, która zwraca 0,35714.
Interpretacja Kappa

Przypadki szczególne
Zgodność mniejsza niż szansa
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
Jeśli wszystkie oceny są takie same i przeciwne
Ten przypadek niezawodnie daje wynik kappa równy 0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
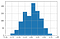
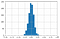
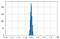
Oceny losowe
Dla ocen losowych Kappa ma rozkład normalny ze średnią około zera.
Wraz ze wzrostem liczby ocen jest mniejsza zmienność wartości Kappa w rozkładzie.
Więcej szczegółów można znaleźć tutaj
Uwaga, że Kappa Cohena ma zastosowanie tylko do dwóch oceniających dokładnie te same pozycje.
