Test Walda: Definition, Examples, Running the Test

Testowanie hipotez >Test Walda

Co to jest test Walda?

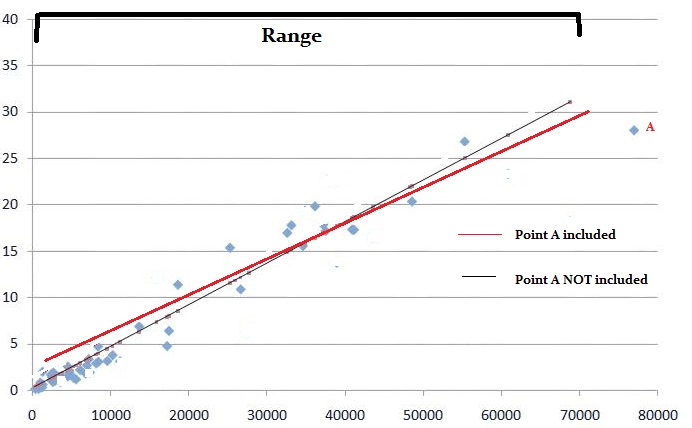
Test Walda może powiedzieć, które zmienne modelu wnoszą coś znaczącego.

Test Walda (zwany również testem Chi-kwadrat Walda) jest sposobem na sprawdzenie, czy zmienne objaśniające w modelu są znaczące. „Istotne” oznacza, że dodają one coś do modelu; zmienne, które nic nie dodają, mogą być usunięte bez wpływu na model w jakikolwiek znaczący sposób. Test może być stosowany dla wielu różnych modeli, w tym tych ze zmiennymi binarnymi lub ciągłymi.
Hipotezą zerową dla testu jest: jakiś parametr = jakaś wartość. Na przykład, możesz badać, czy na wagę wpływa jedzenie śmieciowego jedzenia dwa razy w tygodniu. „Waga” byłaby twoim parametrem. Wartość może wynosić zero (wskazując, że nie sądzisz, że jedzenie śmieciowego jedzenia ma wpływ na wagę). Jeśli hipoteza zerowa zostanie odrzucona, sugeruje to, że zmienne, o których mowa, mogą zostać usunięte bez większego uszczerbku dla dopasowania modelu.

• Jeśli test Walda pokazuje, że parametry dla pewnych zmiennych objaśniających są równe zero, można usunąć te zmienne z modelu.
• Jeśli test pokazuje, że parametry nie są zerowe, powinieneś włączyć te zmienne do modelu.

Test Walda jest zwykle omawiany w kategoriach chi kwadrat, ponieważ rozkład próbkowania (gdy n zbliża się do nieskończoności) jest zwykle znany. Ten wariant testu jest czasami nazywany testem Walda Chi-kwadrat, aby odróżnić go od testu Walda Log-Linear Chi-Square, który jest nieparametrycznym wariantem opartym na log ilorazów szans.

Porównanie do innych testów

Test Walda jest przybliżeniem testu współczynnika prawdopodobieństwa. Jednakże, można go przeprowadzić z jednym modelem (test LR wymaga co najmniej dwóch). Ma on również szersze zastosowanie niż LRT: często można przeprowadzić test Walda w sytuacjach, w których nie można przeprowadzić żadnego innego testu.

Dla dużych wartości n, test Walda jest z grubsza równoważny testowi t; oba testy odrzucają te same wartości dla dużych rozmiarów próbek. Testy Walda, LRT i mnożnika Lagrange’a są równoważne, gdy liczebność próby zbliża się do nieskończoności (nazywane „równoważnymi asymptotycznie”). Jednak próbki o skończonej wielkości, zwłaszcza mniejsze, prawdopodobnie dadzą bardzo różne wyniki.

Agresti (1990) sugeruje, że należy użyć LRT zamiast testu Walda dla małych wielkości próbek lub jeśli parametry są duże. Mała” wielkość próby jest mniejsza niż około 30.

Running the Test

Potrzebujesz pomocy z pytaniem domowym? Sprawdź naszą stronę z korepetycjami!

Wzór na statystykę testu Walda to: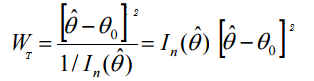

Gdzie:

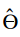• = maksymalny estymator prawdopodobieństwa (MLE),
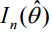• = oczekiwana informacja Fishera (oceniana w MLE).

Podstawowo, test szuka różnic: Θ0 – Θ. Ogólne kroki są następujące:

1. Znajdź MLE.
2. Znajdź oczekiwaną informację Fishera.
3. Oszacuj informację Fishera przy MLE.

Przy kombinacji MLE i informacji Fishera, test Walda jest bardzo złożony w pracy i zazwyczaj nie jest obliczany ręcznie. Wiele programów komputerowych może uruchomić test.

• Stata: użyj polecenia test.
• R: zobacz instrukcje testu WALD dla R (pobierz PDF) z University of Toronto.
• SAS: użyj instrukcji TEST. WALD jest domyślny, jeśli nie określono testu.

Referencje:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.

——————————————————————————

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania krok po kroku na swoje pytania od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!