
Pythagoras of Samos (ok.570-495 BCE)
Biografia – Kim był Pitagoras
Czasami twierdzi się, że czystą matematykę zawdzięczamy Pitagorasowi, i często nazywa się go pierwszym „prawdziwym” matematykiem. Ale, chociaż jego wkład był wyraźnie ważny, pozostaje on postacią kontrowersyjną.
On sam nie pozostawił żadnych pism matematycznych, a wiele z tego, co wiemy o myśli pitagorejskiej pochodzi z pism Filolaosa i innych późniejszych pitagorejskich uczonych. W istocie nie jest jasne, czy wiele (lub w ogóle jakiekolwiek) z przypisywanych mu twierdzeń zostało faktycznie rozwiązanych przez Pitagorasa osobiście lub przez jego zwolenników.
Szkoła, którą założył w Croton w południowych Włoszech około 530 roku p.n.e., była zalążkiem dość dziwacznej sekty pitagorejskiej. Chociaż myśl pitagorejska była w dużej mierze zdominowana przez matematykę, była również głęboko mistyczna, a Pitagoras narzucił swoją quasi-religijną filozofię, ścisły wegetarianizm, życie we wspólnocie, tajemne rytuały i dziwne zasady wszystkim członkom swojej szkoły (w tym dziwaczne i najwyraźniej przypadkowe edykty o tym, by nigdy nie oddawać moczu w kierunku słońca, nigdy nie żenić się z kobietą, która nosi złotą biżuterię, nigdy nie przechodzić obok osła leżącego na ulicy, nigdy nie jeść ani nawet nie dotykać czarnych ziaren faworków itp.
Członkowie podzieleni byli na „mathematikoi” (lub „uczących się”), którzy rozszerzali i rozwijali bardziej matematyczną i naukową pracę, którą rozpoczął sam Pitagoras, oraz „akousmatikoi” (lub „słuchających”), którzy skupiali się na bardziej religijnych i rytualnych aspektach jego nauk. Zawsze istniały pewne tarcia między tymi dwiema grupami, a w końcu sekta została wplątana w zacięte walki lokalne i ostatecznie rozproszyła się. Niechęć narastała przeciwko tajności i ekskluzywności pitagorejczyków i w 460 r. p.n.e. wszystkie ich miejsca spotkań zostały spalone i zniszczone, a co najmniej 50 członków zginęło w samym Croton.
Nadrzędne dictum szkoły Pitagorasa brzmiało: „Wszystko jest liczbą” lub „Bóg jest liczbą”, a pitagorejczycy skutecznie praktykowali rodzaj numerologii lub kultu liczb i uważali, że każda liczba ma swój własny charakter i znaczenie. Na przykład, liczba jeden była generatorem wszystkich liczb; dwa reprezentowały opinię; trzy – harmonię; cztery – sprawiedliwość; pięć – małżeństwo; sześć – stworzenie; siedem – siedem planet lub „wędrujących gwiazd”; itd. Liczby nieparzyste uważano za żeńskie, a parzyste za męskie.
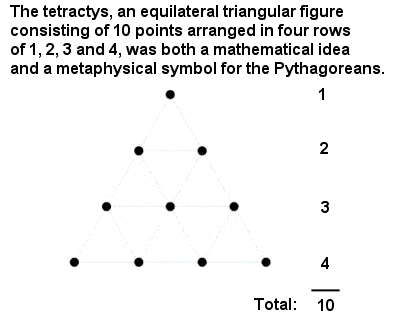
Tetraktys pitagorejski
Najświętszą liczbą ze wszystkich była „Tetraktys” lub dziesięć, liczba trójkątna złożona z sumy jednego, dwóch, trzech i czterech. To wielki hołd dla intelektualnych osiągnięć pitagorejczyków, że wywnioskowali specjalne miejsce liczby 10 z abstrakcyjnego matematycznego argumentu, a nie z czegoś tak prozaicznego jak liczenie palców u dwóch rąk.
Jednakże Pitagoras i jego szkoła – jak również garstka innych matematyków starożytnej Grecji – była w dużej mierze odpowiedzialna za wprowadzenie bardziej rygorystycznej matematyki niż to, co było wcześniej, budując od pierwszych zasad przy użyciu aksjomatów i logiki. Przed Pitagorasem, na przykład, geometria była jedynie zbiorem reguł wyprowadzonych z pomiarów empirycznych.
Pythagoras odkrył, że można skonstruować kompletny system matematyczny, w którym elementy geometryczne odpowiadają liczbom, a liczby całkowite i ich stosunki są wszystkim, co było konieczne do ustanowienia całego systemu logiki i prawdy.
Twierdzenie pitagorejskie
Został zapamiętany głównie dzięki temu, co stało się znane jako Twierdzenie Pitagorasa (lub Twierdzenie pitagorejskie): że dla każdego trójkąta prostokątnego kwadrat długości przeciwprostokątnej (najdłuższego boku, przeciwległego do kąta prostego) jest równy sumie kwadratów dwóch pozostałych boków (lub „nóg”).
Zapisane jako równanie: a2 + b2 = c2.
Choć Pitagoras i jego zwolennicy nie zdawali sobie sprawy, że działa to również dla dowolnego kształtu: tak więc pole pięciokąta na przeciwprostokątnej jest równe sumie pól pięciokątów na pozostałych dwóch bokach, tak samo jak w przypadku półokręgu lub dowolnego innego regularnego (a nawet nieregularnego) kształtu.
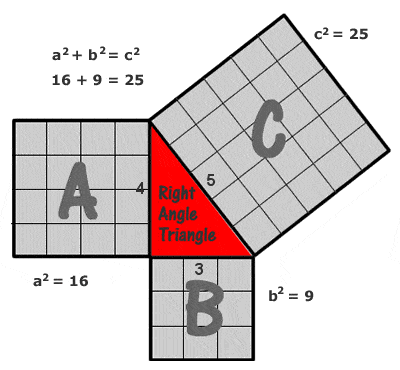
Twierdzenie Pitagorasa
Najprostszym i najczęściej przytaczanym przykładem trójkąta pitagorejskiego jest trójkąt o bokach długości 3, 4 i 5 jednostek (32 + 42 = 52, jak można zobaczyć rysując siatkę kwadratów jednostkowych na każdym boku, jak na rysunku po prawej), ale istnieje potencjalnie nieskończona liczba innych całkowitych „trójkątów pitagorejskich”, począwszy od (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), itd. Należy jednak zauważyć, że (6, 8, 10) nie jest tym, co jest znane jako „prymitywna” trójka pitagorejska, ponieważ jest to po prostu wielokrotność (3, 4, 5).
Twierdzenie Pitagorasa i własności trójkątów prostokątnych wydaje się być najbardziej starożytnym i rozpowszechnionym rozwojem matematycznym po podstawowej arytmetyce i geometrii, i zostało poruszone w niektórych z najbardziej starożytnych tekstów matematycznych z Babilonu i Egiptu, pochodzących z ponad tysiąca lat wcześniej. Jeden z najprostszych dowodów pochodzi ze starożytnych Chin i prawdopodobnie powstał na długo przed narodzinami Pitagorasa. To jednak Pitagoras nadał twierdzeniu jego ostateczną formę, choć nie jest jasne, czy sam Pitagoras ostatecznie je udowodnił, czy tylko opisał. Tak czy inaczej, stało się ono jednym z najbardziej znanych twierdzeń matematycznych, a obecnie istnieje aż 400 różnych dowodów, niektóre geometryczne, niektóre algebraiczne, niektóre obejmujące zaawansowane równania różniczkowe itp.
Wkrótce jednak stało się oczywiste, że możliwe są również rozwiązania niecałkowite, tak że trójkąt równoramienny o bokach 1, 1 i √2, na przykład, ma również kąt prosty, co Babilończycy odkryli wieki wcześniej. Kiedy jednak uczeń Pitagorasa, Hippasus, próbował obliczyć wartość √2, stwierdził, że nie da się jej wyrazić w postaci ułamka, wskazując tym samym na potencjalne istnienie zupełnie nowego świata liczb – liczb irracjonalnych (liczb, których nie da się wyrazić w postaci ułamków zwykłych liczb całkowitych). To odkrycie raczej wstrząsnęło eleganckim matematycznym światem zbudowanym przez Pitagorasa i jego zwolenników, a istnienie liczby, która nie mogła być wyrażona jako stosunek dwóch boskich tworów (tak myśleli o liczbach całkowitych), zagroziło całemu systemowi wierzeń sekty.
Biedny Hippasus został najwyraźniej utopiony przez skrytych pitagorejczyków za rozgłaszanie tego ważnego odkrycia na zewnątrz. Jednak zastąpienie idei boskości liczb całkowitych bogatszym pojęciem kontinuum było istotnym wydarzeniem w matematyce. Oznaczało ono prawdziwe narodziny greckiej geometrii, która zajmuje się liniami, płaszczyznami i kątami, z których wszystkie są ciągłe, a nie dyskretne.
Pośród jego innych osiągnięć w geometrii, Pitagoras (lub przynajmniej jego zwolennicy, pitagorejczycy) również zdał sobie sprawę, że suma kątów trójkąta jest równa dwóm kątom prostym (180°), a prawdopodobnie również uogólnienie, które stwierdza, że suma kątów wewnętrznych wielokąta o n bokach jest równa (2n – 4) kątom prostym, i że suma jego kątów zewnętrznych równa się 4 kątom prostym. Byli w stanie skonstruować figury o danym obszarze, a także używać prostej algebry geometrycznej, na przykład do rozwiązywania równań takich jak a(a – x) = x2 za pomocą środków geometrycznych.
Pitagorejczycy ustanowili również podstawy teorii liczb, z ich badań trójkątów, kwadratów, a także liczb doskonałych (liczby, które są sumą ich dzielników). Odkryli kilka nowych własności liczb kwadratowych, m.in. to, że kwadrat liczby n jest równy sumie pierwszych n liczb nieparzystych (np. 42 = 16 = 1 + 3 + 5 + 7). Odkryli także co najmniej pierwszą parę liczb podzielnych, 220 i 284 (liczby podzielne to pary liczb, dla których suma dzielników jednej liczby jest równa drugiej, np. dzielniki właściwe 220 to 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 i 110, których suma wynosi 284; a dzielniki właściwe 284 to 1, 2, 4, 71 i 142, których suma wynosi 220).
Teoria muzyki
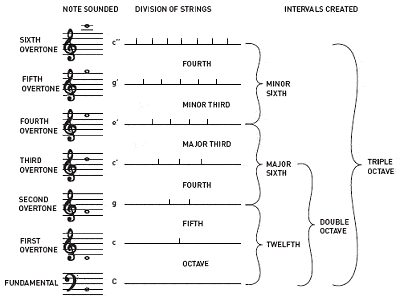
Pythagorasowi przypisuje się odkrycie stosunków między harmonijnymi tonami muzycznymi
Pythagorasowi przypisuje się również odkrycie, że interwały między harmonijnymi nutami muzycznymi zawsze mają stosunki liczb całkowitych. Na przykład, gra na połowie długości struny gitary daje tę samą nutę, co otwarta struna, ale o oktawę wyżej; jedna trzecia długości daje inną, ale harmonijną nutę; itd.
Niepełne proporcje liczb całkowitych, z drugiej strony, mają tendencję do dawania dysonansowych dźwięków. W ten sposób Pitagoras opisał pierwsze cztery overtony, które tworzą wspólne interwały, które stały się podstawowym budulcem harmonii muzycznej: oktawę (1:1), kwintę doskonałą (3:2), kwintę doskonałą (4:3) i tercję wielką (5:4). Najstarszy sposób strojenia 12-nutowej skali chromatycznej znany jest jako strojenie pitagorejskie i opiera się na stosie kwint doskonałych, z których każda strojona jest w stosunku 3:2.
Mistyczny Pitagoras był tak podekscytowany tym odkryciem, że stał się przekonany, iż cały wszechświat opiera się na liczbach, a planety i gwiazdy poruszają się zgodnie z równaniami matematycznymi, które odpowiadają nutom muzycznym, i w ten sposób stworzył rodzaj symfonii, „Musical Universalis” lub „Muzykę Sfer”.
| << Powrót do matematyki greckiej | Przód do Platona >> |
.
