W tym rozdziale zapoznamy się z operacjami na zbiorach i notacjami, tak abyśmy mogli zastosować te pojęcia zarówno do liczenia, jak i do problemów związanych z prawdopodobieństwem. Zaczniemy od zdefiniowania kilku pojęć.
Zbiór jest zbiorem obiektów, a jego członkowie są nazywani elementami zbioru. Nazywamy zbiór używając wielkich liter, a jego elementy ujmujemy w nawiasy klamrowe. Załóżmy, że musimy wypisać członków klubu szachowego. Używamy następującej notacji zbiorów.
C ={Ken, Bob, Tran, Shanti, Eric}
Zbiór, który nie ma członków nazywamy zbiorem pustym. Pusty zbiór oznaczamy symbolem Ø.
Dwa zbiory są równe, jeśli mają te same elementy.
Zbiór A jest podzbiorem zbioru B, jeśli każdy członek A jest również członkiem B.
Załóżmy, że C = {Al, Bob, Chris, David, Ed} i A = {Bob, David}. Wtedy A jest podzbiorem C, zapisanym jako 
.
Każdy zbiór jest podzbiorem samego siebie, a zbiór pusty jest podzbiorem każdego zbioru.
Union Of Two Sets
Let A and B be two sets, then the union of A and B, written as 
, is the set of all elements that are either in A or in B, or in both A and B.
Intersection Of Two Sets
Let A and B be two sets, then the intersection of A and B, written as 
, is the set of all elements that are common to both sets A and B.
A universal set U is the set consisting of all elements under consideration.
Dopełnienie zbioru
Niech A będzie dowolnym zbiorem, wówczas dopełnieniem zbioru A, zapisywanym jako 
, jest zbiór składający się z elementów zbioru uniwersalnego U, które nie występują w A.
Zbiory rozłączne
Dwa zbiory A i B nazywamy zbiorami rozłącznymi, jeśli ich przecięcie jest zbiorem pustym.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {pomarańczowy, zielony, indygo, fioletowy}Aby lepiej zrozumieć, załóżmy, że zbiór uniwersalny U reprezentuje kolory widma, a P kolory podstawowe, to reprezentuje te kolory widma, które nie są kolorami podstawowymi.
.
= {czerwony, żółty, niebieski, zielony}
= {pomarańczowy, indygo, fioletowy}
= {czerwony, żółty, niebieski, fioletowy} = {fioletowy}Diagramy Venna
Do ilustrowania związków między zbiorami używamy teraz diagramów Venna. W późnych latach 1800, angielski logik John Venn opracował metodę reprezentowania relacji między zestawami. Przedstawił te relacje za pomocą diagramów, które są obecnie znane jako diagramy Venna. Diagram Venna przedstawia zbiór jako wnętrze okręgu. Często dwa lub więcej okręgów jest zamkniętych w prostokącie, gdzie prostokąt reprezentuje zbiór uniwersalny. Wizualizacja przecięcia lub unii zbiorów jest prosta. W tym rozdziale będziemy głównie używać diagramów Venna do sortowania różnych populacji i liczenia obiektów.
|
(a) |
(b) |
(c) |
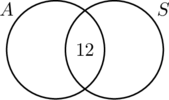
Ponieważ 30 osób jeździło samochodami z automatyczną skrzynią biegów, koło A musi zawierać 30 elementów. Oznacza to, że x + 12 = 30, czyli x = 18. Podobnie, ponieważ 20 osób jeździło samochodami ze standardową skrzynią biegów, koło B musi zawierać 20 elementów, czyli y +12 = 20, co z kolei daje y = 8.
Teraz, gdy wszystkie informacje są uporządkowane, łatwo odczytać z diagramu, że 18 osób jeździło samochodami tylko z automatyczną skrzynią biegów, 12 osób jeździło obydwoma typami samochodów, a 8 jeździło samochodami tylko ze standardową skrzynią biegów. Zatem w ankiecie wzięło udział 18 + 12 + 8 = 38 osób.
|
(a) |
(b) |
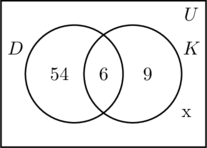
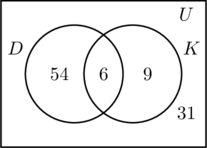
Wypełniamy trzy regiony związane ze zbiorami D i K w taki sam sposób jak poprzednio. Ponieważ w ankiecie wzięło udział 100 osób, to prostokąt reprezentujący zbiór uniwersalny U musi zawierać 100 obiektów. Niech x reprezentuje te osoby ze zbioru uniwersalnego, które nie znajdują się ani w zbiorze D, ani w K. Oznacza to, że 54 + 6 + 9 + x = 100, czyli x = 31.
Więc w ankiecie wzięło udział 31 osób, które nie odwiedziły żadnego z tych miejsc.
- 50 biega, 30 pływa i 35 jeździ na rowerze
- 14 biega i pływa
- 7 pływa i jeździ na rowerze
- 9 biega i jeździ na rowerze
- 3 osoby biorą udział we wszystkich trzech aktywnościach
Rozwiązanie
|
(a) |
(b) |
(c) . |
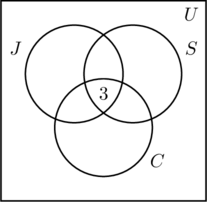
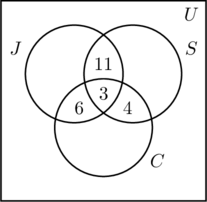
Umieszczamy trójkę w najbardziej wewnętrznym regionie rysunku (a), ponieważ reprezentuje ona liczbę osób, które uczestniczą we wszystkich trzech aktywnościach. Następnie obliczamy x, y i z.
- Ponieważ 14 osób biega i pływa, x +3 = 14, czyli x = 11.
- Z faktu, że 9 osób biega i jeździ na rowerze wynika, że y + 3 = 9, czyli y = 6.
- Skoro 7 osób pływa i jeździ na rowerze, to z + 3 = 7, czyli z = 4.
- Informacja ta jest przedstawiona na rysunku (b).
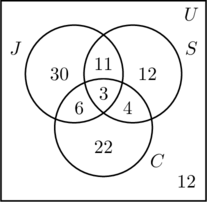
- Ponieważ 50 osób biega, m + 11 + 6 + 3 = 50, czyli m = 30.
- 30 osób pływa, zatem n + 11 + 4 + 3 = 30, lub n = 12.
- 35 osób jeździ na rowerze, zatem p + 6 + 4 + 3 = 35, lub p = 22.
- Dodając do siebie wszystkie zapisy we wszystkich trzech zbiorach, otrzymujemy sumę 88. Ponieważ przebadano 100 osób, liczba wewnątrz zbioru uniwersalnego, ale poza wszystkimi trzema zbiorami, wynosi 100 – 88, czyli 12.
- Na rysunku (c) informacje są uporządkowane, a na pytania można łatwo odpowiedzieć.
Pytania praktyczne
1. Niech zbiór uniwersalny U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, oraz W = {a, c, e, g, i}. Wymień członków następujących zbiorów:
a. 
b. 
2. Rozważmy następujące zbiory: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Grypa, Norowirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norowirus, Shigella} oraz C = {SARS, Listeria, Gruźlica, H5N1, Salmonella, HIV, COVID-19}. Wymień członków następujących zestawów:
a. 
b. 
3. Ankieta przeprowadzona wśród sportowców wykazała, że na ich drobne bóle 30 używało aspiryny, 50 używało ibuprofenu, a 15 używało obu tych środków. Wszyscy badani sportowcy używali co najmniej jednego z tych dwóch leków przeciwbólowych. Ilu sportowców wzięło udział w badaniu?
4. Badanie 150 uczniów szkół średnich wykazało, że 25 zgłosiło, że miało wcześniej wstrząs mózgu lub uraz głowy, 52 zgłosiło, że doświadczyło choroby psychicznej, a 15 zgłosiło oba te zdarzenia. Ilu uczniów nie zgłosiło żadnego z tych wyników?
5. Ankieta przeprowadzona wśród 100 studentów Uniwersytetu Ryerson wykazała, że 50 z nich subskrybuje Netflix, 40 subskrybuje Amazon Prime, a 30 subskrybuje Disney+. Spośród nich 15 subskrybuje zarówno Netflix, jak i Amazon Prime, 10 zarówno Amazon Prime, jak i Disney+, 10 zarówno Netflix, jak i Disney+, a 5 posiada wszystkie trzy usługi subskrypcji. Narysuj diagram Venna i ustal, co następuje:
a. Liczba studentów korzystających z Amazon Prime, ale nie korzystających z dwóch pozostałych usług streamingowych.
b. Liczba studentów subskrybujących Netflix lub Amazon Prime, ale nie Disney+.
c. Liczba studentów, którzy nie subskrybują żadnej z tych usług.
c.