Grupa 
jest skończonym lub nieskończonym zbiorem elementów wraz z operacją binarną (zwaną operacją grupową), które razem spełniają cztery podstawowe własności zamknięcia, asocjatywności, własności tożsamości i własności odwrotności. Operacja, w odniesieniu do której definiuje się grupę, jest często nazywana „operacją grupową”, a o zbiorze mówi się, że jest grupą „pod” tą operacją. Elementy 
, 
, 
, … z operacją binarną między 
i 
oznaczoną 
tworzą grupę, jeśli
1. Domknięcie: Jeśli 
i 
są dwoma elementami w 
, to iloczyn 
jest również w 
.
2. asocjatywność: Zdefiniowane mnożenie jest asocjacyjne, tzn. dla wszystkich 
, 
.
3. identyczność: Istnieje element tożsamości 
(vel 1, 
, lub 
) taki, że 
dla każdego elementu 
.
4. inwersja: Musi istnieć odwrotność (a.k.a. reciprocal) każdego elementu. Dlatego dla każdego elementu 
z 
, zbiór zawiera element 
taki, że 
.
Grupa jest monoidem, którego każdy z elementów jest odwracalny.
Grupa musi zawierać co najmniej jeden element, z unikalną (do izomorfizmu) jednoelementową grupą znaną jako grupa trywialna.
Badanie grup znane jest jako teoria grup. Jeśli istnieje skończona liczba elementów, grupa jest nazywana grupą skończoną, a liczba elementów jest nazywana porządkiem grupy. Podzbiór grupy, który jest zamknięty na operację grupową i operację odwrotną, nazywamy podgrupą. Podgrupy są również grupy, a wiele powszechnie spotykanych grup są w rzeczywistości specjalne podgrupy niektórych bardziej ogólnych większych group.
Podstawowym przykładem grupy skończonej jest grupa symetryczna 
, która jest grupą permutacji (lub „pod permutacji”) 
obiektów. Najprostszą grupą nieskończoną jest zbiór liczb całkowitych w zwykłym dodawaniu. Dla grup ciągłych można rozważać liczby rzeczywiste lub zbiór 
macierzy odwracalnych. Te dwie ostatnie są przykładami grup Lie.
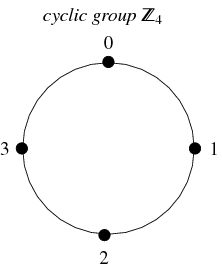
Jednym z bardzo często spotykanych typów grup są grupy cykliczne. Grupa ta jest izomorficzna z grupą liczb całkowitych (modulo 
), jest oznaczana 
, 
lub 
i jest określona dla każdej liczby całkowitej 
. Jest ona zamknięta w dodawaniu, asocjacyjna i ma unikalne odwrotności. Liczby od 0 do 
reprezentują jej elementy, z elementem tożsamości reprezentowanym przez 0, a odwrotność 
jest reprezentowana przez 
.
Mapa między dwiema grupami, która zachowuje tożsamość i operację grupową nazywana jest homomorfizmem. Jeśli homomorfizm ma odwrotność, która jest również homomorfizmem, to jest nazywany izomorfizmem, a dwie grupy są nazywane izomorficzne. Dwie grupy, które są izomorficzne do siebie są uważane za „takie same”, gdy są postrzegane jako grupy abstrakcyjne. Na przykład, grupa obrotów kwadratu, zilustrowana poniżej, jest grupą cykliczną 
.
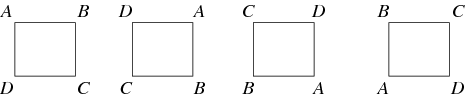
Ogólnie, działanie grupowe jest wtedy, gdy grupa działa na zbiór, permutując jego elementy, tak że mapa z grupy na grupę permutacji zbioru jest homomorfizmem. Na przykład, obroty kwadratu są podgrupą permutacji jego narożników. Jednym z ważnych działań grupowych dla każdej grupy 
jest jej działanie na siebie przez koniugację. To są tylko niektóre z możliwych automorfizmów grupowych. Innym ważnym rodzajem działania grupowego jest reprezentacja grupy, gdzie grupa działa na przestrzeni wektorowej przez odwracalne mapy liniowe. Gdy pole przestrzeni wektorowej jest liczbami zespolonymi, czasami reprezentacja nazywana jest modułem CG.
Działania grupowe, a w szczególności reprezentacje, są bardzo ważne w zastosowaniach, nie tylko w teorii grup, ale także w fizyce i chemii. Ponieważ grupa może być postrzegana jako abstrakcyjny obiekt matematyczny, ta sama grupa może pojawić się w różnych kontekstach. Dlatego warto myśleć o reprezentacji grupy jako o jednym szczególnym wcieleniu grupy, która może mieć także inne reprezentacje. Nieredukowalna reprezentacja grupy jest reprezentacją, dla której nie istnieje jednostkowe przekształcenie, które przekształci macierz reprezentacji do postaci blokowej diagonalnej. Reprezentacje nieredukowalne mają szereg niezwykłych własności, które zostały sformułowane w twierdzeniu o ortogonalności grupy.
.