Cele nauczania
Do końca tego rozdziału, będziesz w stanie:
- Opisać typowy eksperyment z efektem fotoelektrycznym.
- Określić maksymalną energię kinetyczną fotoelektronów wyrzuconych przez fotony o jednej energii lub długości fali, gdy podano maksymalną energię kinetyczną fotoelektronów dla innej energii fotonu lub długości fali.
Gdy światło uderza w materiały, może wyrzucać z nich elektrony. Nazywa się to efektem fotoelektrycznym, co oznacza, że światło (foto) wytwarza energię elektryczną. Jednym z powszechnych zastosowań efektu fotoelektrycznego są światłomierze, takie jak te, które regulują automatyczną przysłonę w różnych typach aparatów fotograficznych. W podobny sposób efekt ten jest wykorzystywany w ogniwach słonecznych, które prawdopodobnie masz w swoim kalkulatorze, widziałeś na dachu lub na znaku drogowym. Wykorzystują one efekt fotoelektryczny do przekształcania światła w energię elektryczną do zasilania różnych urządzeń.

Rysunek 1. Efekt fotoelektryczny można zaobserwować, pozwalając światłu padać na metalową płytkę w tej próżniowej rurce. Elektrony wyrzucone przez światło są zbierane na drucie kolektorowym i mierzone jako prąd. Napięcie opóźniające pomiędzy przewodem zbierającym a płytką może być następnie regulowane w taki sposób, aby określić energię wyrzucanych elektronów. Na przykład, jeśli jest ono wystarczająco ujemne, żadne elektrony nie dotrą do drutu. (credit: P.P. Urone)
Efekt ten jest znany od ponad wieku i może być badany przy użyciu urządzenia takiego jak to pokazane na rysunku 1. Rysunek ten przedstawia próżniową rurkę z metalową płytką i drutem kolektora, które są połączone zmiennym źródłem napięcia, przy czym kolektor jest bardziej ujemny niż płytka. Kiedy światło (lub inne promieniowanie EM) uderza w płytkę w rurze próżniowej, może ono wyrzucić elektrony. Jeżeli elektrony te mają energię w elektronowoltach (eV) większą niż różnica potencjałów między płytą a przewodem w woltach, to część elektronów zostanie zgromadzona na przewodzie. Ponieważ energia elektronów w eV to eV, gdzie q to ładunek elektronu, a V to różnica potencjałów, energię elektronów można zmierzyć regulując napięcie opóźniające pomiędzy drutem a płytką. Napięcie, które powstrzymuje elektrony przed dotarciem do drutu równa się energii w eV. Na przykład, jeżeli -3,00 V ledwo zatrzymuje elektrony, ich energia wynosi 3,00 eV. Liczba wyrzuconych elektronów może być określona poprzez pomiar prądu pomiędzy drutem a płytką. Im więcej światła, tym więcej elektronów; niewielki obwód pozwala na użycie tego urządzenia jako światłomierza.
To, co jest naprawdę ważne o efekcie fotoelektrycznym, to to, co Albert Einstein z niego wywnioskował. Einstein zdał sobie sprawę, że istnieje kilka cech efektu fotoelektrycznego, które mogą być wyjaśnione tylko wtedy, gdy promieniowanie EM jest samo w sobie skwantowane: pozornie ciągły strumień energii w fali EM jest w rzeczywistości złożony z kwantów energii zwanych fotonami. W swoim wyjaśnieniu efektu fotoelektrycznego, Einstein zdefiniował skwantowaną jednostkę lub kwant energii EM, który obecnie nazywamy fotonem, o energii proporcjonalnej do częstotliwości promieniowania EM. W postaci równania, energia fotonu to E = hf, gdzie E jest energią fotonu o częstotliwości f, a h jest stałą Plancka. Ten rewolucyjny pomysł wygląda podobnie do kwantowania stanów energetycznych przez Plancka w oscylatorach ciała doskonale czarnego, ale jest zupełnie inny. Jest to kwantyzacja samego promieniowania EM. Fale EM składają się z fotonów i nie są ciągłymi, gładkimi falami, jak to opisano w poprzednich rozdziałach o optyce. Ich energia jest pochłaniana i emitowana w bryłach, a nie w sposób ciągły. Jest to dokładnie zgodne z planckowską kwantyzacją poziomów energetycznych w oscylatorach ciała doskonale czarnego, ponieważ oscylatory te zwiększają i zmniejszają swoją energię w krokach co hf poprzez pochłanianie i emitowanie fotonów o energii E = hf. Nie obserwujemy tego za pomocą naszych oczu, ponieważ w zwykłych źródłach światła jest tak wiele fotonów, że pojedyncze fotony pozostają niezauważone. (Patrz rysunek 2.) Następna część tekstu (Energie fotonów i widmo elektromagnetyczne) poświęcona jest omówieniu fotonów i niektórych ich właściwości oraz implikacji. Na razie użyjemy koncepcji fotonu do wyjaśnienia efektu fotoelektrycznego, podobnie jak zrobił to Einstein.
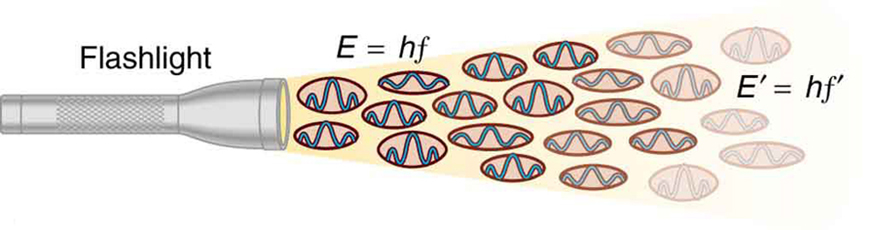
Rysunek 2. Fala EM o częstotliwości f składa się z fotonów, czyli pojedynczych kwantów promieniowania EM. Energia każdego fotonu wynosi E = hf, gdzie h jest stałą Plancka, a f jest częstotliwością promieniowania EM. Większe natężenie oznacza więcej fotonów na jednostkę powierzchni. Latarka emituje dużą liczbę fotonów o wielu różnych częstotliwościach, stąd inne mają energię E′ = hf′, i tak dalej.
Efekt fotoelektryczny ma właściwości omówione poniżej. Wszystkie te własności są zgodne z ideą, że poszczególne fotony promieniowania EM są absorbowane przez poszczególne elektrony w materiale, przy czym elektron zyskuje energię fotonu. Niektóre z tych własności są sprzeczne z ideą, że promieniowanie EM jest prostą falą. Dla uproszczenia rozważmy, co dzieje się z monochromatycznym promieniowaniem EM, w którym wszystkie fotony mają tę samą energię hf.
- Jeśli zmienimy częstotliwość promieniowania EM padającego na materiał, stwierdzimy, co następuje: Dla danego materiału istnieje częstotliwość progowa f0 dla promieniowania EM, poniżej której nie są wyrzucane żadne elektrony, niezależnie od natężenia. Poszczególne fotony oddziałują z poszczególnymi elektronami. Jeśli więc energia fotonu jest zbyt mała, aby oderwać elektron, to żaden elektron nie zostanie wyrzucony. Gdyby promieniowanie EM było prostą falą, wystarczającą energię można by uzyskać przez zwiększenie natężenia.
- Gdy promieniowanie EM pada na materiał, elektrony są wyrzucane bez zwłoki. Gdy tylko pojedynczy foton o dostatecznie wysokiej częstotliwości zostanie pochłonięty przez pojedynczy elektron, zostaje on wyrzucony. Gdyby promieniowanie EM było prostą falą, potrzeba by było kilku minut, aby na powierzchni metalu osadziła się energia wystarczająca do wyrzucenia elektronu.
- Liczba elektronów wyrzuconych w jednostce czasu jest proporcjonalna do natężenia promieniowania EM i do żadnej innej cechy. Promieniowanie EM o dużym natężeniu składa się z dużej liczby fotonów na jednostkę powierzchni, przy czym wszystkie fotony mają tę samą energię charakterystyczną hf.
- Jeśli zmienimy natężenie promieniowania EM i zmierzymy energię wyrzuconych elektronów, stwierdzimy, co następuje: Maksymalna energia kinetyczna wyrzuconych elektronów jest niezależna od natężenia promieniowania EM. Ponieważ w materiale jest tak wiele elektronów, jest bardzo mało prawdopodobne, że dwa fotony będą oddziaływać z tym samym elektronem w tym samym czasie, zwiększając w ten sposób jego energię. Zamiast tego (jak zauważono w punkcie 3 powyżej), zwiększone natężenie powoduje wyrzucenie większej ilości elektronów o tej samej energii. Gdyby promieniowanie EM było prostą falą, większe natężenie mogłoby dać więcej energii, a elektrony o wyższej energii zostałyby wyrzucone.
- Energia kinetyczna wyrzuconego elektronu równa się energii fotonu minus energia wiązania elektronu w danym materiale. Pojedynczy foton może oddać całą swoją energię elektronowi. Energia fotonu jest częściowo wykorzystywana do oderwania elektronu od materiału. Pozostała część idzie na energię kinetyczną wyrzuconego elektronu. W formie równania, jest to dane przez KEe = hf – BE, gdzie KEe jest maksymalną energią kinetyczną wyrzuconego elektronu, hf jest energią fotonu, a BE jest energią wiązania elektronu z danym materiałem. (BE jest czasami nazywane funkcją pracy materiału). Równanie to, którego autorem jest Einstein w 1905 roku, wyjaśnia ilościowo właściwości efektu fotoelektrycznego. Pojedynczy foton promieniowania elektromagnetycznego (nie dociera ono w inny sposób) oddziałuje z pojedynczym elektronem, dostarczając mu wystarczającą ilość energii, BE, aby go oderwać, a pozostała część idzie na energię kinetyczną. Energia wiązania wynosi BE = hf0, gdzie f0 jest częstotliwością progową dla danego materiału. Rysunek 3 przedstawia wykres maksymalnej KEe w funkcji częstotliwości padającego promieniowania EM na dany materiał.
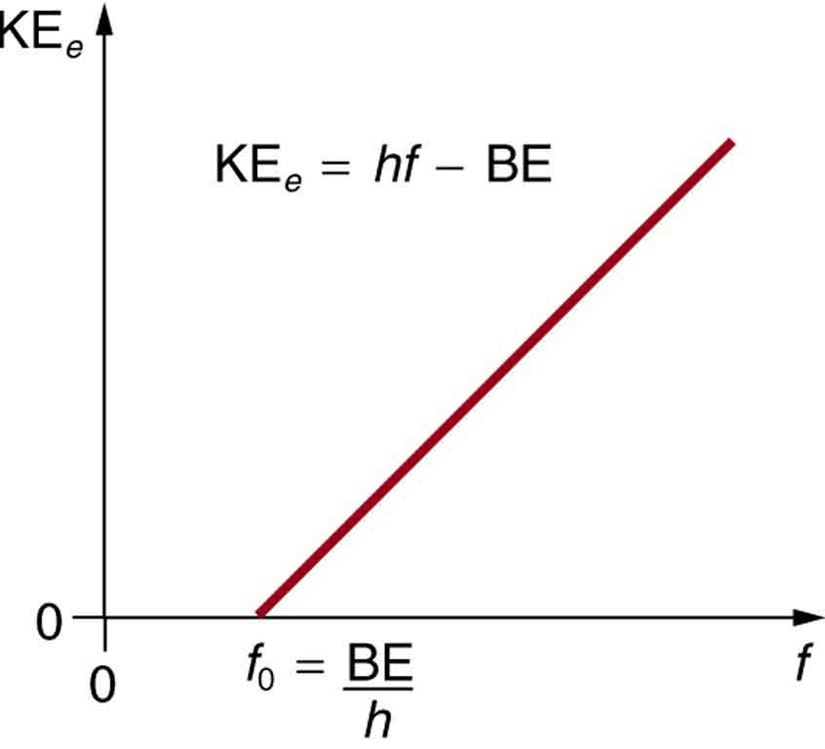
Rysunek 3. Efekt fotoelektryczny. Wykres energii kinetycznej wyrzuconego elektronu, KEe, w funkcji częstotliwości promieniowania EM padającego na dany materiał. Istnieje częstotliwość progowa, poniżej której nie są wyrzucane elektrony, ponieważ pojedynczy foton oddziałujący z pojedynczym elektronem ma niewystarczającą energię, aby go oderwać. Powyżej energii progowej, KEe rośnie liniowo z f, zgodnie z KEe = hf – BE. Nachylenie tej linii to h – dane te mogą być użyte do eksperymentalnego wyznaczenia stałej Plancka. Einstein podał pierwsze udane wyjaśnienie takich danych, proponując ideę fotonów – kwantów promieniowania EM.
Pomysł Einsteina, że promieniowanie EM jest skwantowane, był kluczowy dla początków mechaniki kwantowej. Jest to koncepcja o wiele bardziej ogólna niż mogłoby to sugerować wyjaśnienie efektu fotoelektrycznego. Całe promieniowanie EM może być również modelowane w postaci fotonów, a charakterystyka promieniowania EM jest całkowicie zgodna z tym faktem. (Jak zobaczymy w następnym rozdziale, wiele aspektów promieniowania EM, takich jak zagrożenia związane z promieniowaniem ultrafioletowym (UV), można wyjaśnić jedynie poprzez właściwości fotonów). Einstein, bardziej znany z nowoczesnej teorii względności, zasiał ważne ziarno dla mechaniki kwantowej w 1905 r., w tym samym roku, w którym opublikował swoją pierwszą pracę na temat szczególnej teorii względności. Jego wyjaśnienie efektu fotoelektrycznego było podstawą do przyznania mu Nagrody Nobla w 1921 roku. Choć w nagrodzie tej odnotowano także inne jego zasługi dla fizyki teoretycznej, szczególna i ogólna teoria względności nie zostały w pełni uznane, mimo że do 1921 r. zostały częściowo zweryfikowane eksperymentalnie. Chociaż czczony jako bohater, ten wielki człowiek nigdy nie otrzymał Nobla za swoją najsłynniejszą pracę – względność.
Przykład 1. Obliczanie energii fotonu i efektu fotoelektrycznego: Fioletowe światło
1. Jaka jest energia w dżulach i elektronowoltach fotonu fioletowego światła o długości fali 420 nm?
2. Jaka jest maksymalna energia kinetyczna elektronów wyrzuconych z wapnia przez fioletowe światło o długości fali 420 nm, biorąc pod uwagę, że energia wiązania (lub funkcja pracy) elektronów dla metalu wapnia wynosi 2,71 eV?
Strategia
Aby rozwiązać część 1, zauważ, że energia fotonu jest dana wzorem E = hf. Dla części 2, po obliczeniu energii fotonu, jest to proste zastosowanie KEe = hf – BE, aby znaleźć maksymalną energię kinetyczną wyrzuconego elektronu, ponieważ BE jest dane.
Rozwiązanie dla części 1
Energia fotonu jest dana przez E = hf.
Ponieważ dana jest nam długość fali, a nie częstotliwość, rozwiązujemy znaną zależność c = fλ dla częstotliwości, otrzymując f= hfrac{c}{lambda}.
Połączenie tych dwóch równań daje użyteczną zależność E= hfrac{hc}{lambda}.
Teraz podstawiając znane wartości otrzymujemy
displaystyle{E}= E=frac{left(6.63\times10^{-34}\text{ J}}prawa)\left(3.00times10^{8}}text{ m/s}}}}=4.74times10^{-19}}text{ J}}
Przeliczając na eV, energia fotonu wynosi
displaystyle{E}=}left(4.\frac{1}}{1.6\times10^{-19}\text{ J}}=2.96\text{ eV}
Rozwiązanie dla części 2
Znalezienie energii kinetycznej wyrzuconego elektronu jest teraz prostym zastosowaniem równania KEe = hf – BE. Podstawiając energię fotonu i energię wiązania otrzymujemy KEe = hf – BE = 2.96 eV – 2.71 eV = 0.246 eV.
Dyskusja
Energia tego 420-nm fotonu fioletowego światła jest maleńkim ułamkiem dżula, więc nic dziwnego, że pojedynczy foton byłby dla nas trudny do bezpośredniego wyczucia – ludzie są bardziej przyzwyczajeni do energii rzędu dżuli. Ale patrząc na energię w elektronowoltach, widzimy, że ten foton ma wystarczającą energię, aby oddziaływać na atomy i cząsteczki. Na przykład, cząsteczka DNA może zostać rozbita przy energii około 1 eV, a typowe energie atomowe i molekularne są rzędu eV, więc foton UV w tym przykładzie może mieć efekty biologiczne. Wyrzucony elektron (zwany fotoelektronem) ma raczej niską energię i nie podróżowałby daleko, chyba że w próżni. Elektron zostałby zatrzymany przez potencjał opóźniający o wartości zaledwie 0.26 eV. W rzeczywistości, gdyby długość fali fotonu była większa, a jego energia mniejsza niż 2.71 eV, wtedy wzór dałby ujemną energię kinetyczną, co jest niemożliwe. Oznacza to po prostu, że fotony o długości fali 420 nm i energii 2,96 eV niewiele przekraczają próg częstotliwości. Można samemu wykazać, że progowa długość fali wynosi 459 nm (światło niebieskie). Oznacza to, że jeśli w światłomierzu zastosuje się metaliczny wapń, to nie będzie on wrażliwy na fale dłuższe niż światło niebieskie. Taki światłomierz byłby całkowicie niewrażliwy na światło czerwone, na przykład.
PhET Explorations: Photoelectric Effect
Zobacz, jak światło wybija elektrony z metalowego celu, i odtwórz eksperyment, który dał początek dziedzinie mechaniki kwantowej.

Kliknij, aby pobrać symulację. Uruchom przy użyciu języka Java.
Spis treści
- Efekt fotoelektryczny to proces, w którym promieniowanie EM wyrzuca elektrony z materiału.
- Einstein zaproponował, aby fotony były kwantami promieniowania EM o energii E = hf, gdzie f jest częstotliwością promieniowania.
- Wszystkie promieniowanie EM składa się z fotonów. Jak wyjaśnił Einstein, wszystkie cechy efektu fotoelektrycznego wynikają z interakcji poszczególnych fotonów z poszczególnymi elektronami.
- Maksymalna energia kinetyczna KEe wyrzuconych elektronów (fotoelektronów) jest dana przez KEe = hf – BE, gdzie hf jest energią fotonu, a BE jest energią wiązania (lub funkcją pracy) elektronu do danego materiału.
Pytania pojęciowe
- Czy światło widzialne jest jedynym rodzajem promieniowania EM, które może wywołać efekt fotoelektryczny?
- Które aspekty efektu fotoelektrycznego nie mogą być wyjaśnione bez fotonów? Które mogą być wyjaśnione bez fotonów? Czy te ostatnie są sprzeczne z istnieniem fotonów?
- Czy efekt fotoelektryczny jest bezpośrednią konsekwencją falowego charakteru promieniowania EM lub cząsteczkowego charakteru promieniowania EM? Wyjaśnij krótko.
- Insulatory (niemetale) mają wyższy BE niż metale, i trudniej jest dla fotonów do wyrzucenia elektronów z izolatorów. Omów, jak to się odnosi do wolnych ładunków w metalach, które czynią je dobrymi przewodnikami.
- Jeśli podnieść i potrząsnąć kawałek metalu, który ma elektrony w nim swobodnie poruszać się jako prąd, nie elektrony wypadają. Jednak jeśli podgrzejesz metal, elektrony mogą zostać wygotowane. Wyjaśnij oba te fakty, ponieważ dotyczą one ilości i rozkładu energii związanej ze wstrząsaniem obiektu w porównaniu z jego ogrzewaniem.
Problemy &Ćwiczenia
- Jaka jest najdłuższa długość fali promieniowania EM, które może wyrzucić fotoelektron ze srebra, biorąc pod uwagę, że energia wiązania wynosi 4,73 eV? Czy jest to zakres widzialny?
- Znajdź foton o najdłuższej długości fali, który może wyrzucić elektron z potasu, biorąc pod uwagę, że energia wiązania wynosi 2,24 eV. Czy jest to widzialne promieniowanie EM?
- Jaka jest energia wiązania w eV elektronów w magnezie, jeżeli foton o najdłuższej długości fali, który może wyrzucić elektrony, ma długość 337 nm?
- Oblicz energię wiązania w eV elektronów w aluminium, jeżeli foton o najdłuższej długości fali, który może je wyrzucić, ma długość 304 nm.
- Jaka jest maksymalna energia kinetyczna w eV elektronów wyrzuconych z metalu sodowego przez 450-nm promieniowanie EM, jeśli energia wiązania wynosi 2,28 eV?
- Promieniowanie UV o długości fali 120 nm pada na metal złoty, z którym elektrony są związane przez 4,82 eV. Jaka jest maksymalna energia kinetyczna wyrzuconych fotoelektronów?
- Światło fioletowe o długości fali 400 nm wyrzuca z metalu sodu elektrony o maksymalnej energii kinetycznej 0,860 eV. Jaka jest energia wiązania elektronów z metalem sodu?
- Promieniowanie UV o długości fali 300 nm pada na metal uranu, wyrzucając elektrony o energii 0,500 eV. Jaka jest energia wiązania elektronów z metalem uranu?
- (a) Jaka jest długość fali promieniowania EM, które wyrzuca elektrony o energii 2.00-eV z metalu wapnia, biorąc pod uwagę, że energia wiązania wynosi 2.71 eV? (b) Jaki to rodzaj promieniowania EM?
- Znajdź długość fali fotonów, które wyrzucają elektrony o energii 0,100-eV z potasu, biorąc pod uwagę, że energia wiązania wynosi 2,24 eV. Czy te fotony są widoczne?
- Jaka jest maksymalna prędkość elektronów wyrzucanych z materiału przez fotony o długości fali 80-nm, jeśli są one związane z materiałem przez 4,73 eV?
- Fotelektrony z materiału o energii wiązania 2,71 eV są wyrzucane przez fotony o długości fali 420-nm. Po wyrzuceniu, ile czasu zajmuje tym elektronom przebycie drogi 2,50 cm do urządzenia detekcyjnego?
- Laser o mocy 2,00 mW przy długości fali 400 nm jest rzutowany na metal wapnia. (a) Ile elektronów na sekundę jest wyrzucanych? (b) Jaka moc jest przenoszona przez elektrony, biorąc pod uwagę, że energia wiązania wynosi 2,71 eV?
- (a) Oblicz liczbę fotoelektronów na sekundę wyrzucanych z 1,00-mm 2 powierzchni metalu sodowego przez 500-nm promieniowanie EM o natężeniu 1,30 kW/m2 (natężenie światła słonecznego nad atmosferą ziemską). (b) Biorąc pod uwagę, że energia wiązania wynosi 2,28 eV, jaka moc jest przenoszona przez elektrony? (c) Elektrony przenoszą mniejszą moc niż ta, którą wniosły fotony. Gdzie trafia pozostała moc? Jak można ją odzyskać?
- Nieuzasadnione wyniki. Czerwone światło o długości fali 700 nm pada na metal magnezu, z którym elektrony są związane przez 3,68 eV. (a) Użyj KEe = hf – BE do obliczenia energii kinetycznej wyrzuconych elektronów. (b) Co jest nieuzasadnione w tym wyniku? (c) Które założenia są nieracjonalne lub niespójne?
- Nieracjonalne wyniki. (a) Jaka jest energia wiązania elektronów w materiale, z którego elektrony o energii 4.00-eV są wyrzucane przez promieniowanie EM o długości fali 400-nm? (b) Co jest nieuzasadnione w tym wyniku? (c) Które założenia są nieracjonalne lub niespójne?
Słownik
efekt fotoelektryczny: zjawisko, dzięki któremu niektóre materiały wyrzucają elektrony, gdy pada na nie światło
foton: kwant lub cząstka promieniowania elektromagnetycznego
energia fotonu: ilość energii, jaką posiada foton; E = hf
energia wiązania: zwana również funkcją pracy; ilość energii niezbędna do wyrzucenia elektronu z materiału
Wybrane rozwiązania problemów &Ćwiczenia
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm; (b) ultrafiolet
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) ujemna energia kinetyczna; (c) elektrony zostaną uwolnione
.
