Science > Physics > Photoelectric Effect >Einstein’s Photoelectric Equation
W tym artykule, będziemy, derive Einstein’s photoelectric equation and study its use to verify the characteristics of the photoelectric effect of light.
Falowa natura światła:
Christian Huygen’s zaproponował, że światło rozchodzi się w formie fali. Ale ta teoria ma poważną wadę. Nie był w stanie wyjaśnić propagacji światła w próżni. Wada ta została usunięta przez Maxwella, który zaproponował, że światło jest falą elektromagnetyczną, a do rozchodzenia się fal elektromagnetycznych nie jest potrzebny żaden ośrodek materialny. W ten sposób została ustalona falowa natura światła.
Teoria falowa była w stanie wyjaśnić wszystkie zjawiska związane z propagacją światła. Nie potrafiła jednak wyjaśnić rozkładu energii i współczesnych zjawisk takich jak efekt fotoelektryczny, efekt Cromptona itp.
Cząsteczkowa natura światła:
Max Planck udowodnił, że propagacja światła lub energii odbywa się w postaci pakietów energii zwanych kwantami. Kwant światła nazywany jest fotonem i w ten sposób ustalił on cząsteczkową naturę światła. Wykorzystując cząstkową lub kwantową naturę promieniowania możemy wyjaśnić zjawisko efektu fotoelektrycznego i efektu Cromptona.
Teoria kwantowa Plancka:
Teoria kwantowa została zaproponowana przez Maxa Plancka. Zgodnie z tą teorią, promieniowanie ze źródła nie jest emitowane w sposób ciągły, ale jest emitowane w pakietach lub wiązkach energii. Pakiety te nazywane są kwantami lub fotonami. Jeśli promieniowanie ma częstotliwość ν, to każdy kwant ma energię, gdzie h jest stałą Plancka.
Tym samym energia fotonu = E = hν
Energia jest emitowana w sposób nieciągły. Jest to sprzeczne z teorią klasyczną, która zakłada, że emisja energii jest procesem ciągłym.
Cząsteczkowa natura promieniowania elektromagnetycznego:
W interakcji promieniowania z materią, promieniowanie zachowuje się tak, jakby było zbudowane z cząstek. Cząstki te nazywane są fotonami. Każdy foton ma energię, która jest dana przez
E = hν = hc/λ
Wszystkie fotony światła o określonej częstotliwości (długości fali) ma taką samą ilość energii z nimi związane. Wzrost natężenia światła zwiększa liczbę fotonów na sekundę przechodzących przez dany obszar, ale energia każdego fotonu będzie taka sama. Fotony są elektrycznie neutralne i nie mają na nie wpływu pola elektryczne ani magnetyczne. Fotony podróżują w linii prostej z prędkością światła „c”, ale wykazują dyfrakcję w pewnych warunkach.
Pęd każdego fotonu jest dany przez
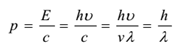
Długość fali fotonu zmienia się w zależności od mediów, stąd mają one różne prędkości w różnych mediach. Masa spoczynkowa fotonu wynosi zero. Its kineticmass is given by
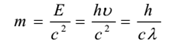
In photon particle collision (such as a photon-electron collision) the total energy and momentum are conserved. Jednak liczba fotonów może nie być zachowana w zderzeniu. Foton może zostać zaabsorbowany lub może powstać nowy foton.
Równanie fotoelektryczne Einsteina:
Na podstawie kwantowej teorii Plancka, Einstein wyprowadził równanie dla efektu fotoelektrycznego znane jako równanie fotoelektryczne Einsteina. Einstein założył, że
- Światło składa się z fotonów lub kwantów energii, energia w każdym fotonie wynosi hν. Gdzie h jest stałą Plancka, a ν jest częstotliwością światła
- Każdy padający foton zderza się z elektronem wewnątrz atomu i oddaje całą swoją energię elektronowi.
- Część tej energii jest wykorzystywana przez elektron do wyjścia z powierzchni metalu, a pozostała część jest energią kinetyczną, z którą elektron jest emitowany.
- Minimalna energia wymagana przez elektron do wyjścia z powierzchni metalu jest nazywana fotoelektryczną funkcją pracy (∅o) metalu.
Więc, maksymalna energia kinetyczna elektronu = energia fotonu – funkcja pracy
Niech 'm’ będzie masą elektronu, a vmax maksymalną prędkością fotoelektronu, z jaką zostanie on wyrzucony.

Równanie to znane jest jako równanie fotoelektryczne Einsteina
Funkcja pracy fotoelektrycznej:
W efekcie fotoelektrycznym, najbardziej luźno związany elektron atomu materiału światłoczułego jest usuwany. Minimalna energia potrzebna do uwolnienia elektronu z danej powierzchni nazywana jest fotoelektryczną funkcją pracy (∅o) materiału powierzchni. Funkcja pracy jest charakterystyczną właściwością powierzchni metalu.
Matematycznie funkcja pracy jest dana wzorem
∅o = h νo
Gdzie νo = częstotliwość progowa i h =stała Plancka.
Wyjaśnienie istnienia częstotliwości progowej na podstawie równania fotoelektrycznego Einsteina:
Dla danej powierzchni metalicznej fotoelektrony są emitowane tylko wtedy, gdy częstotliwość padającego światła jest większa lub równa pewnej minimalnej częstotliwości (no)zwanej częstotliwością progową. The threshold frequency is different fordifferent Substances,
By Einstein’s photoelectric equation

Where νo = Threshold frequencyand h = Planck’s constant and
ν = frequency of incident radiation
The kinetic energy is always non-negative quantity i.tj. może być dodatnia lub zerowa, a więc

Wskazuje to, że dla efektu fotoelektrycznego częstotliwość padającego promieniowania lub padającego fotonu powinna być równa lub większa od częstotliwości progowej. Siła przyciągania działająca na prawdopodobne fotoelektrony w różnych atomach jest różna. Dlatego częstotliwość progowa jest różna dla różnych substancji.
Wyjaśnienie efektu natężenia na podstawie równania fotoelektrycznego Einsteina:
Jeśli częstotliwość padającego światła jest mniejsza od częstotliwości progowej, fotoelektrony nie są emitowane, niezależnie od tego, jak duże może być natężenie padającego światła.
Liczba fotoelektronów emitowanych w ciągu sekundy jest wprost proporcjonalna do natężenia padającego światła. Tak więc prąd fotoelektryczny jest wprost proporcjonalny do natężenia padającego światła. Jeśli natężenie światła jest większe, liczba fotonów padających na powierzchnię jest większa. Ze względu na zwiększoną liczbę fotoelektronów wzrasta szybkość fotoemisji, a tym samym siła prądu fotoelektrycznego. Można więc stwierdzić, że efekt fotoelektryczny (prąd) jest wprost proporcjonalny do natężenia padającego promieniowania.
Wyjaśnienie możliwej maksymalnej energii kinetycznej na podstawie równania fotoelektrycznego Einsteina:
Przez równanie fotoelektryczne Einsteina

gdzie νo = częstotliwość progowa i h = stała Plancka oraz
ν = częstotliwość padającego promieniowania
Równanie to nie zawiera pojęcia natężenia, Można więc powiedzieć, że maksymalna energia kinetyczna fotoelektronu jest niezależna od natężenia promieniowania padającego, ale zależy od częstotliwości promieniowania padającego. Z nierówności tej wynika, że maksymalna energia kinetyczna elektronu zależy od częstości padającego promieniowania. I jeśli częstotliwość promieniowania jest zwiększona, energia kinetyczna fotoelektronu również wzrasta.
Wyjaśnienie natychmiastowości efektu fotoelektrycznego na podstawie równania fotoelektrycznego Einsteina:
Efekt fotoelektryczny jest procesem natychmiastowym. Nie ma opóźnienia czasowego pomiędzy padaniem światła a emisją fotoelektronów, innymi słowy, powierzchnia zaczyna emitować fotoelektrony natychmiast po padnięciu na nią światła. Również emisja fotoelektronów zatrzymuje się w momencie odcięcia padającego światła.
Gdy promieniowanie pada na powierzchnię fotoemitującą w tym momencie, cała energia fotonu jest przekazywana pojedynczemu elektronowi za jednym zamachem. Tak więc elektron zostaje wyemitowany bez żadnego opóźnienia czasowego i efekt fotoelektryczny jest procesem natychmiastowym.
Poprzedni Temat: Problemy numeryczne dotyczące efektu fotoelektrycznego
Next Topic: Numerical Problems on Photoelectric Equation
Nauka > Fizyka >Efekt fotoelektryczny >Równanie fotoelektryczne Einsteina
.
