Schemat fazowy wody
Rysunek 11.23 „Dwie wersje diagramu fazowego wody” przedstawia diagram fazowy wody i ilustruje, że punkt potrójny wody występuje w temperaturze 0,01°C i ciśnieniu 0,00604 atm (4,59 mmHg). O wiele bardziej powtarzalny niż temperatura topnienia lodu, która zależy od ilości rozpuszczonego powietrza i ciśnienia atmosferycznego, punkt potrójny (273,16 K) jest używany do definiowania skali temperatury bezwzględnej (Kelvina). Punkt potrójny reprezentuje również najniższe ciśnienie, przy którym faza ciekła może istnieć w równowadze ze stałą lub parą. Dlatego przy ciśnieniu niższym niż 0,00604 atm lód nie topi się w ciecz wraz ze wzrostem temperatury; ciało stałe sublimuje bezpośrednio do pary wodnej. Sublimacja wody w niskiej temperaturze i pod niskim ciśnieniem może być wykorzystywana do „liofilizacji” żywności i napojów. Żywność lub napoje są najpierw schładzane do temperatury poniżej zera i umieszczane w pojemniku, w którym ciśnienie jest utrzymywane na poziomie poniżej 0,00604 atm. Następnie, wraz ze wzrostem temperatury, woda sublimuje, pozostawiając odwodniony pokarm (taki jak ten używany przez backpackerów lub astronautów) lub sproszkowany napój (jak w przypadku liofilizowanej kawy).
Schemat fazowy wody przedstawiony w części (b) na rysunku 11.23 „Dwie wersje schematu fazowego wody” pokazuje granicę między lodem a wodą w rozszerzonej skali. Krzywa topnienia lodu opada w górę i lekko w lewo, a nie w górę i w prawo, jak na rysunku 11.22 „Typowy diagram fazowy substancji, która wykazuje trzy fazy – stałą, ciekłą i gazową – oraz obszar nadkrytyczny”; to znaczy, że temperatura topnienia lodu maleje wraz ze wzrostem ciśnienia; przy ciśnieniu 100 MPa (987 atm) lód topi się w temperaturze -9°C. Woda zachowuje się w ten sposób, ponieważ jest jedną z niewielu znanych substancji, dla których krystaliczne ciało stałe ma mniejszą gęstość niż ciecz (inne to antymon i bizmut). Zwiększenie ciśnienia lodu znajdującego się w równowadze z wodą w temperaturze 0°C i ciśnieniu 1 atm powoduje zbliżenie do siebie niektórych cząsteczek, co zmniejsza objętość próbki. Zmniejszenie objętości (i odpowiadający mu wzrost gęstości) jest mniejsze dla ciała stałego lub cieczy niż dla gazu, ale wystarcza do stopienia części lodu.
Rysunek 11.23 Dwie wersje diagramu fazowego wody
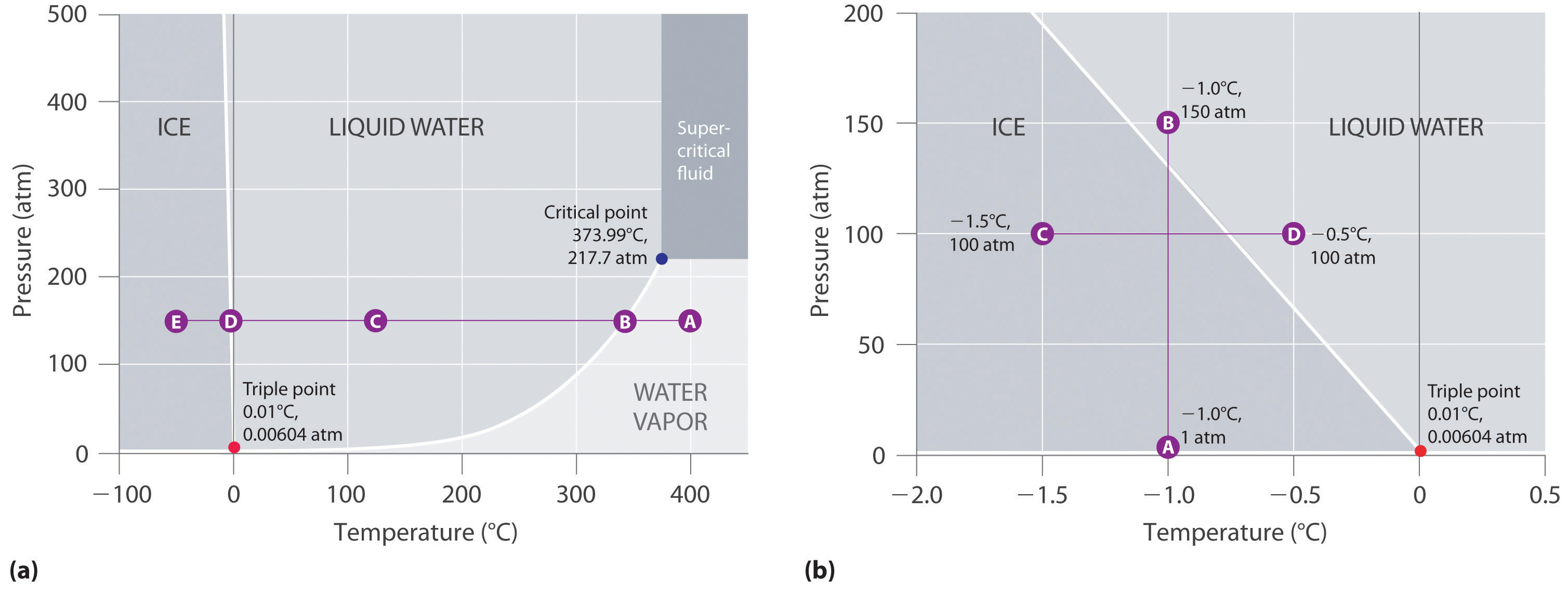
(a) Na tym wykresie z liniowymi osiami temperatury i ciśnienia granica między lodem a ciekłą wodą jest prawie pionowa. (b) Ten wykres z rozszerzoną skalą ilustruje obniżanie się temperatury topnienia wraz ze wzrostem ciśnienia. (Litery odnoszą się do punktów omówionych w przykładzie 10.)
W części (b) na rysunku 11.23 „Dwie wersje diagramu fazowego wody”, punkt A znajduje się przy P = 1 atm i T = -1,0°C, w regionie ciała stałego (lodu) na diagramie fazowym. Gdy ciśnienie wzrasta do 150 atm, podczas gdy temperatura pozostaje taka sama, linia z punktu A przecina granicę lód/woda do punktu B, który leży w obszarze wody w stanie ciekłym. W związku z tym, zastosowanie ciśnienia 150 atm spowoduje stopienie lodu o temperaturze -1,0°C. Zaznaczyliśmy już, że zależność temperatury topnienia wody od ciśnienia ma istotne znaczenie. Gdyby granica ciało stałe/ciecz na diagramie fazowym wody była nachylona w górę i w prawo, a nie w lewo, lód byłby gęstszy od wody, kostki lodu tonęłyby, rury wodociągowe nie pękałyby, gdy zamarzają, a płyn niezamarzający byłby niepotrzebny w silnikach samochodowych.
Do niedawna wiele podręczników opisywało jazdę na łyżwach jako możliwą, ponieważ ciśnienie wytwarzane przez ostrze łyżwiarza jest wystarczająco wysokie, aby stopić lód pod ostrzem, tworząc w ten sposób smarującą warstwę ciekłej wody, która umożliwia ostrzu ślizganie się po lodzie. Chociaż to wyjaśnienie jest intuicyjnie satysfakcjonujące, jest ono błędne, co możemy pokazać za pomocą prostych obliczeń. Przypomnijmy sobie z rozdziału 10 „Gazy”, że ciśnienie (P) to siła (F) przyłożona na jednostkę powierzchni (A):
Równanie 11.4
P = F A
Aby obliczyć ciśnienie wywierane przez łyżwiarza na lód, musimy obliczyć tylko wywieraną siłę i powierzchnię ostrza łyżwy. Jeśli założymy, że łyżwiarz waży 75 kg, to siła wywierana przez niego na lód z powodu grawitacji wynosi
Równanie 11.5
F = mg
gdzie m to masa, a g to przyspieszenie ziemskie (9,81 m/s2). Zatem siła wynosi
Równanie 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Jeśli przyjmiemy, że ostrza łyżew mają szerokość 2.0 mm szerokości i 25 cm długości, to powierzchnia spodu każdego ostrza wynosi
Równanie 11.7
A = (2.0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Jeśli łyżwiarz ślizga się na jednej nodze, ciśnienie wywierane na lód wynosi
Równanie 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Ciśnienie to jest znacznie niższe od ciśnienia potrzebnego do obniżenia temperatury topnienia lodu nawet o 1°C, a doświadczenie wskazuje, że jazda na łyżwach jest możliwa nawet przy temperaturze znacznie poniżej zera. Zatem topnienie lodu wywołane ciśnieniem nie może tłumaczyć niskiego tarcia, które umożliwia łyżwiarzom (i krążkom hokejowym) ślizganie się. Najnowsze badania wskazują, że powierzchnia lodu, gdzie uporządkowany układ cząsteczek wody styka się z powietrzem, składa się z jednej lub więcej warstw prawie płynnej wody. Te warstwy, wraz z topnieniem wywołanym przez tarcie, gdy łyżwiarz posuwa się do przodu, wydają się tłumaczyć zarówno łatwość, z jaką łyżwiarz się ślizga, jak i fakt, że jazda na łyżwach staje się trudniejsza poniżej około -7°C, gdy liczba smarujących warstw wody powierzchniowej maleje.
.
