Bayesian information criterion (BIC) jest kryterium wyboru modelu spośród skończonego zbioru modeli. Jest ono oparte, częściowo, na funkcji prawdopodobieństwa i jest blisko spokrewnione z kryterium informacyjnym Akaike (AIC).
Podczas dopasowywania modeli możliwe jest zwiększenie prawdopodobieństwa poprzez dodanie parametrów, ale takie postępowanie może prowadzić do przepasowania. BIC rozwiązuje ten problem poprzez wprowadzenie karnego terminu dla liczby parametrów w modelu. BIC jest większy w BIC niż w AIC.
BIC był szeroko stosowany do identyfikacji modeli w szeregach czasowych i regresji liniowej. Może być jednak stosowany dość szeroko do dowolnego zbioru modeli opartych na maksymalnym prawdopodobieństwie.
Matematycznie BIC może być zdefiniowany jako.
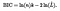

Zastosowanie & Interpretacja:
Modele mogą być testowane przy użyciu odpowiadających im wartości BIC. Niższa wartość BIC wskazuje na niższe warunki karne, stąd lepszy model.
Przeczytaj również statystykę AIC.
Chociaż te dwie miary pochodzą z innej perspektywy, są one ściśle powiązane. Najwyraźniej jedyna różnica polega na tym, że BIC uwzględnia liczbę obserwacji we wzorze, czego nie robi AIC.
Chociaż BIC jest zawsze wyższy niż AIC, niższa wartość tych dwóch miar oznacza lepszy model.
Praktyczne zbiory danych:
Odwiedź naszą platformę do nauki i analizy danych, Analyttica TreasureHunt, aby poćwiczyć na prawdziwych zbiorach danych.
Przeczytaj również:
Sprawdzanie zgodności.
Filtr jądrowy.
k-Means Clustering.
.
