In dit deel zullen we ons vertrouwd maken met setbewerkingen en notaties, zodat we deze concepten kunnen toepassen op zowel tel- als kansproblemen. We beginnen met het definiëren van enkele begrippen.
Een verzameling is een verzameling van voorwerpen, en de leden ervan worden de elementen van de verzameling genoemd. We geven de verzameling een naam in hoofdletters, en sluiten de leden in tussen gekrulde haakjes. Stel dat we een lijst moeten maken van de leden van de schaakclub. We gebruiken de volgende notatie voor de verzameling.
C ={Ken, Bob, Tran, Shanti, Eric}
Een verzameling die geen leden heeft, heet een lege verzameling. De lege verzameling wordt aangeduid met het symbool Ø.
Twee verzamelingen zijn gelijk als ze dezelfde elementen hebben.
Een verzameling A is een deelverzameling van een verzameling B als elk lid van A ook een lid van B is.
Voorstel C = {Al, Bob, Chris, David, Ed} en A = {Bob, David}. Dan is A een deelverzameling van C, geschreven als 
.
Elke verzameling is een deelverzameling van zichzelf, en de lege verzameling is een deelverzameling van elke verzameling.
Eenheid van twee verzamelingen
Zetten A en B twee verzamelingen, dan is de vereniging van A en B, geschreven als 
, de verzameling van alle elementen die óf in A óf in B, óf in zowel A als B zitten.
Samensnijding van twee verzamelingen
Zijn A en B twee verzamelingen, dan is de doorsnede van A en B, geschreven als 
, de verzameling van alle elementen die in beide verzamelingen A en B voorkomen.
Een universele verzameling U is de verzameling die bestaat uit alle elementen die men beschouwt.
Complement van een verzameling
Laat A een willekeurige verzameling zijn, dan is het complement van verzameling A, geschreven als 
, de verzameling bestaande uit elementen in de universele verzameling U die niet in A voorkomen.
Disjuncte verzamelingen
Twee verzamelingen A en B heten disjuncte verzamelingen als hun intersectie een lege verzameling is.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {oranje, groen, indigo, violet}Voor een beter begrip, stel dat de universele verzameling U de kleuren van het spectrum voorstelt, en P de primaire kleuren, dan stelt die kleuren van het spectrum voor die geen primaire kleuren zijn.
.
= {rood, geel, blauw, groen}
= {oranje, indigo, violet}
= {rood, geel, blauw, violet} = {violet}Venn-diagrammen
We gebruiken nu Venn-diagrammen om de relaties tussen verzamelingen te illustreren. In de late jaren 1800 ontwikkelde de Engelse logicus John Venn een methode om relaties tussen verzamelingen weer te geven. Hij stelde deze relaties voor met behulp van diagrammen, die nu bekend staan als Venn-diagrammen. Een Venn-diagram stelt een verzameling voor als het binnenste van een cirkel. Vaak worden twee of meer cirkels omsloten door een rechthoek, waarbij de rechthoek de universele verzameling voorstelt. Het visualiseren van een intersectie of union van een verzameling is eenvoudig. In dit gedeelte zullen we Venn-diagrammen vooral gebruiken om verschillende populaties te sorteren en objecten te tellen.
|
(a) |
(b) |
(c) |
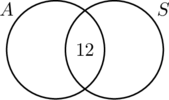
Omdat 30 mensen in auto’s met een automatische versnellingsbak reden, moet de cirkel A 30 elementen bevatten. Dit betekent dat x + 12 = 30, of x = 18. En omdat 20 mensen in auto’s met een standaard transmissie reden, moet cirkel B 20 elementen bevatten, oftewel y +12 = 20, waardoor y = 8.
Nu alle informatie op een rijtje is gezet, valt uit het diagram af te lezen dat 18 mensen in auto’s met alleen een automatische transmissie reden, 12 mensen in beide soorten auto’s, en 8 mensen in auto’s met alleen een standaard transmissie. Er hebben dus 18 + 12 + 8 = 38 mensen aan de enquête deelgenomen.
|
(a) |
(b) |
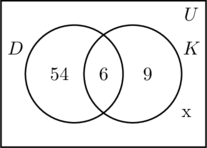
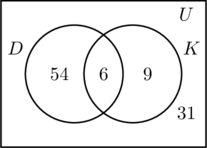
We vullen de drie gebieden die bij de verzamelingen D en K horen op dezelfde manier als voorheen. Aangezien 100 mensen aan de enquête hebben deelgenomen, moet de rechthoek die de universele verzameling U voorstelt 100 objecten bevatten. Laat x staan voor de personen in de universele verzameling die noch in de verzameling D, noch in de verzameling K voorkomen. Dit betekent dat 54 + 6 + 9 + x = 100, of x = 31.
Dus zijn er 31 personen in de enquête die geen van beide plaatsen hebben bezocht.
- 50 joggen, 30 zwemmen, en 35 fietsen
- 14 joggen en zwemmen
- 7 zwemmen en fietsen
- 9 joggen en fietsen
- 3 mensen doen aan alle drie de activiteiten
Oplossing
|
(a) |
(b) |
(c) |
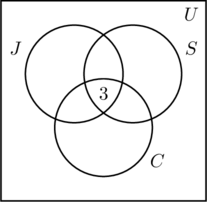
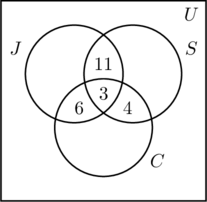
We plaatsen een 3 in het binnenste gebied van figuur (a) omdat dit het aantal mensen vertegenwoordigt dat aan alle drie de activiteiten deelneemt. Vervolgens berekenen we x, y en z.
- Aangezien 14 mensen joggen en zwemmen, is x +3 = 14, of x = 11.
- Het feit dat 9 mensen joggen en fietsen levert y + 3 = 9 op, of y = 6.
- Omdat 7 mensen zwemmen en fietsen, is z + 3 = 7, of z = 4.
- Deze informatie is weergegeven in figuur (b).
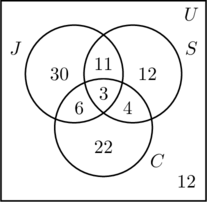
- Omdat 50 mensen joggen, resulteert m + 11 + 6 + 3 = 50, of m = 30.
- 30 mensen zwemmen, dus n + 11 + 4 + 3 = 30, of n = 12.
- 35 mensen fietsen, dus p + 6 + 4 + 3 = 35, of p = 22.
- Door alle gegevens in de drie reeksen op te tellen, krijgen we een som van 88. Aangezien 100 mensen werden geënquêteerd, is het aantal binnen de universele verzameling maar buiten de drie verzamelingen 100 – 88, of 12.
- In figuur (c) is de informatie geordend, en kunnen de vragen gemakkelijk worden beantwoord.
Oefenvragen
1. Zij de universele verzameling U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, en W = {a, c, e, g, i}. Maak een lijst van de leden van de volgende verzamelingen:
a. 
b. 
2. Beschouw de volgende verzamelingen: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, en C = {SARS, Listeria, Tuberculosis, H5N1, Salmonella, HIV, COVID-19}. Maak een lijst van de leden van de volgende verzamelingen:
a. 
b. 
3. Uit een enquête onder sporters bleek dat voor hun kleine pijntjes 30 aspirine gebruikten, 50 ibuprofen, en 15 beide. Alle ondervraagde atleten gebruikten ten minste een van de twee pijnstillers. Hoeveel atleten werden ondervraagd?
4. Uit een onderzoek onder 150 middelbare scholieren bleek dat 25 rapporteerden eerder een hersenschudding of hoofdletsel te hebben gehad, 52 rapporteerden een psychische aandoening te hebben gehad, en 15 rapporteerden beide uitkomsten. Hoeveel studenten meldden geen van beide uitkomsten?
5. Uit een enquête onder 100 studenten aan de Ryerson University blijkt dat 50 geabonneerd zijn op Netflix, 40 op Amazon Prime en 30 op Disney+. Hiervan zijn er 15 geabonneerd op zowel Netflix als Amazon Prime, 10 op zowel Amazon Prime als Disney+, 10 op zowel Netflix als Disney+, en 5 hebben alle drie de abonnementsdiensten. Teken een Venn-diagram en bepaal het volgende:
a. Het aantal studenten met een abonnement op Amazon Prime maar niet op de andere twee streamingdiensten.
b. Het aantal studenten dat geabonneerd is op Netflix of Amazon Prime, maar niet op Disney+.
c. Het aantal studenten dat geen abonnement heeft op een van deze diensten.