
Pythagoras van Samos (c.570-495 BCE)
Biografie – Wie was Pythagoras
Er wordt wel beweerd dat we de zuivere wiskunde te danken hebben aan Pythagoras, en hij wordt vaak de eerste “echte” wiskundige genoemd. Maar, hoewel zijn bijdrage duidelijk belangrijk was, blijft hij toch een controversiële figuur.
Hij heeft zelf geen wiskundige geschriften nagelaten, en veel van wat wij weten over het Pythagorese denken komt tot ons uit de geschriften van Philolaus en andere latere Pythagorese geleerden. Het is zelfs helemaal niet duidelijk of veel (of zelfs geen) van de stellingen die aan hem worden toegeschreven in feite door Pythagoras zelf of door zijn volgelingen zijn opgelost.
De school die hij rond 530 v. Chr. in Croton in Zuid-Italië stichtte, vormde de kern van een nogal bizarre Pythagorese sekte. Hoewel het Pythagorese denken grotendeels door de wiskunde werd beheerst, was het ook diep mystiek, en Pythagoras legde zijn quasi-religieuze filosofieën, strikte vegetarisme, gemeenschappelijk leven, geheime riten en vreemde regels op aan alle leden van zijn school (inclusief bizarre en schijnbaar willekeurige voorschriften over het nooit urineren in de richting van de zon, het nooit trouwen met een vrouw die gouden sieraden draagt, het nooit passeren van een ezel die op straat ligt, het nooit eten of zelfs maar aanraken van zwarte fava bonen, etc) .
De leden werden verdeeld in de “mathematikoi” (of “leerlingen”), die het meer wiskundige en wetenschappelijke werk dat Pythagoras zelf begonnen was, uitbreidden en ontwikkelden, en de “akousmatikoi” (of “toehoorders”), die zich concentreerden op de meer religieuze en ritualistische aspecten van zijn leringen. Er was altijd een zekere wrijving tussen de twee groepen en uiteindelijk raakte de sekte verwikkeld in een aantal hevige plaatselijke gevechten en viel uiteindelijk uiteen. Er ontstond wrevel tegen de geheimhouding en exclusiviteit van de Pythagoreeërs en in 460 v. Chr. werden al hun ontmoetingsplaatsen in brand gestoken en verwoest, waarbij alleen al in Croton minstens 50 leden werden gedood.
Het allesoverheersende dictaat van Pythagoras’ school was “Alles is getal” of “God is getal”, en de Pythagoreeërs beoefenden in feite een soort numerologie of getallenaanbidding, en beschouwden elk getal als een getal met een eigen karakter en betekenis. Zo was het getal één de generator van alle getallen; twee stond voor mening; drie voor harmonie; vier voor rechtvaardigheid; vijf voor huwelijk; zes voor schepping; zeven voor de zeven planeten of “dwalende sterren”; enz. Oneven getallen werden als vrouwelijk beschouwd en even getallen als mannelijk.
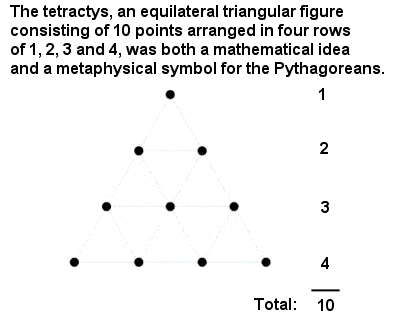
De Pythagoreïsche Tetractys
Het heiligste getal van allen was “Tetractys” of tien, een driehoekig getal bestaande uit de som van één, twee, drie en vier. Het is een groot eerbetoon aan de intellectuele prestaties van de Pythagoreeërs dat zij de speciale plaats van het getal 10 hebben afgeleid uit een abstract wiskundig argument in plaats van uit iets alledaags als het tellen van de vingers van twee handen.
Hoe dan ook, Pythagoras en zijn school – evenals een handvol andere wiskundigen uit het oude Griekenland – waren grotendeels verantwoordelijk voor de invoering van een strengere wiskunde dan wat er tot dan toe was geweest, waarbij werd uitgegaan van de eerste beginselen met gebruikmaking van axioma’s en logica. Vóór Pythagoras, bijvoorbeeld, was de meetkunde niet meer dan een verzameling regels die door empirische metingen was afgeleid.
Pythagoras ontdekte dat een compleet systeem van wiskunde kon worden geconstrueerd, waarin meetkundige elementen overeenkwamen met getallen, en waarin gehele getallen en hun verhoudingen alles waren wat nodig was om een compleet systeem van logica en waarheid op te zetten.
De stelling van Pythagoras
Hij wordt vooral herinnerd om wat bekend is geworden als de stelling van Pythagoras (of de stelling van Pythagoras): dat voor elke rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (de langste zijde, tegenover de rechte hoek) gelijk is aan de som van het kwadraat van de andere twee zijden (of “benen”).
Verschreven als een vergelijking: a2 + b2 = c2.
Wat Pythagoras en zijn volgelingen zich niet realiseerden is dat dit ook voor elke vorm werkt: de oppervlakte van een pentagon op de schuine zijde is dus gelijk aan de som van de pentagons op de andere twee zijden, net zoals dat geldt voor een halve cirkel of elke andere regelmatige (of zelfs onregelmatige) vorm.
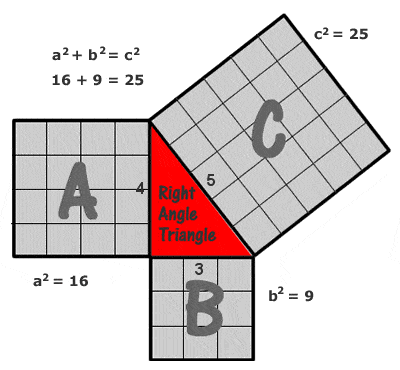
De stelling van Pythagoras
Het eenvoudigste en meest geciteerde voorbeeld van een Pythagoras-driehoek is er een met zijden van 3, 4 en 5 eenheden (32 + 42 = 52, zoals te zien is door een rooster van eenheidsvierkanten te tekenen op elke zijde zoals in het diagram rechts), maar er zijn een potentieel oneindig aantal andere gehele “Pythagoras-driehoeken”, te beginnen met (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), enz. Opgemerkt moet echter worden dat (6, 8, 10) niet wat men noemt een “primitief” Pythagoreïsch drietal is, want het is slechts een veelvoud van (3, 4, 5).
De Stelling van Pythagoras en de eigenschappen van rechthoekige driehoeken schijnt de oudste en wijdst verbreide wiskundige ontwikkeling te zijn na basisrekenen en meetkunde, en werd aangestipt in enkele van de oudste wiskundige teksten uit Babylon en Egypte, daterend van meer dan duizend jaar eerder. Een van de eenvoudigste bewijzen komt uit het oude China, en dateert waarschijnlijk van ver voor de geboorte van Pythagoras. Het was echter Pythagoras die de stelling zijn definitieve vorm gaf, hoewel het niet duidelijk is of Pythagoras hem zelf definitief bewees of slechts beschreef. Hoe dan ook, het is een van de bekendste wiskundige stellingen geworden, en er bestaan nu wel 400 verschillende bewijzen, sommige meetkundig, sommige algebraïsch, sommige met geavanceerde differentiaalvergelijkingen, enz.
Toen bleek echter dat ook niet-integere oplossingen mogelijk waren, zodat bijvoorbeeld een gelijkbenige driehoek met zijden 1, 1 en √2 ook een rechte hoek heeft, zoals de Babyloniërs eeuwen eerder al hadden ontdekt. Toen de leerling van Pythagoras, Hippasus, echter probeerde de waarde van √2 te berekenen, ontdekte hij dat het niet mogelijk was deze uit te drukken als een breuk, waarmee hij wees op het mogelijke bestaan van een geheel nieuwe getallenwereld, de irrationale getallen (getallen die niet kunnen worden uitgedrukt als eenvoudige breuken van gehele getallen). Deze ontdekking verbrijzelde de elegante wiskundige wereld die was opgebouwd door Pythagoras en zijn volgelingen, en het bestaan van een getal dat niet kon worden uitgedrukt als de verhouding van twee van Gods scheppingen (wat zij dachten van de gehele getallen) bracht het hele geloofssysteem van de cultus in gevaar.
De arme Hippasus zou door de geheimzinnige Pythagoreeërs zijn verdronken omdat hij deze belangrijke ontdekking aan de buitenwereld had bekendgemaakt. Maar de vervanging van het idee van de goddelijkheid van de gehele getallen door het rijkere concept van het continuüm, was een essentiële ontwikkeling in de wiskunde. Het betekende de echte geboorte van de Griekse meetkunde, die zich bezighoudt met lijnen en vlakken en hoeken, die alle continu en niet discreet zijn.
Naast zijn andere prestaties in de meetkunde, realiseerde Pythagoras (of althans zijn volgelingen, de Pythagoreeërs) zich ook dat de som van de hoeken van een driehoek gelijk is aan twee rechte hoeken (180°), en waarschijnlijk ook de veralgemening die stelt dat de som van de binnenhoeken van een veelhoek met n zijden gelijk is aan (2n – 4) rechte hoeken, en dat de som van de buitenhoeken gelijk is aan 4 rechte hoeken. Zij waren in staat figuren met een gegeven oppervlakte te construeren, en eenvoudige meetkundige algebra te gebruiken, bijvoorbeeld om vergelijkingen als a(a – x) = x2 met meetkundige middelen op te lossen.
De Pythagoreeërs legden ook de grondslagen van de getaltheorie, met hun onderzoek van driehoekige, vierkante en ook volmaakte getallen (getallen die de som zijn van hun delers). Zij ontdekten verschillende nieuwe eigenschappen van kwadratische getallen, zoals dat het kwadraat van een getal n gelijk is aan de som van de eerste n oneven getallen (b.v. 42 = 16 = 1 + 3 + 5 + 7). Zij ontdekten ook ten minste het eerste paar amicale getallen, 220 en 284 (amicale getallen zijn getallenparen waarvan de som van de delers van het ene getal gelijk is aan het andere getal, b.v. de eigen delers van 220 zijn 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 en 110, waarvan de som 284 is; en de eigen delers van 284 zijn 1, 2, 4, 71, en 142, waarvan de som 220 is).
Muziektheorie
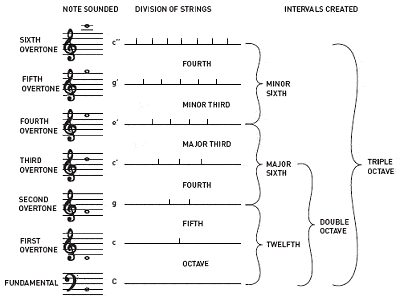
Pythagoras wordt de ontdekking van de verhoudingen tussen harmonische muziektonen toegedicht
Pythagoras wordt ook de ontdekking toegedicht dat de intervallen tussen harmonische muzieknoten altijd verhoudingen van gehele getallen hebben. Zo geeft het bespelen van een halve gitaarsnaar dezelfde toon als de open snaar, maar dan een octaaf hoger; een derde van een snaarlengte geeft een andere, maar harmonische toon; enz.
Niet-gehele getalsverhoudingen daarentegen, geven meestal dissonante klanken. Op deze manier beschreef Pythagoras de eerste vier boventonen die de gemeenschappelijke intervallen creëren die de primaire bouwstenen van de muzikale harmonie zijn geworden: het octaaf (1:1), de reine kwint (3:2), de reine kwart (4:3) en de grote terts (5:4). De oudste manier om de chromatische toonladder met 12 tonen te stemmen staat bekend als de Pythagoreïsche stemming, en is gebaseerd op een stapeling van reine kwinten, elk gestemd in de verhouding 3:2.
De mystieke Pythagoras was zo opgewonden door deze ontdekking dat hij ervan overtuigd raakte dat het hele universum gebaseerd was op getallen, en dat de planeten en sterren bewogen volgens wiskundige vergelijkingen, die overeenkwamen met muzieknoten, en zo een soort symfonie voortbracht, de “Musical Universalis” of “Muziek van de Sferen”.
| << Terug naar de Griekse wiskunde | Voorwaarts naar Plato >> |
