We weten hoe we de vierkantswortel van elk positief reeel getal kunnen vinden. Op een vergelijkbare manier kunnen we de vierkantswortel van een negatief getal vinden. Het verschil is dat de wortel niet reëel is. Als de waarde in de radicand negatief is, is de wortel een imaginair getal. Het imaginaire getal i is gedefinieerd als de vierkantswortel van negatief 1.
Met behulp van de eigenschappen van de radikalen kunnen we dus de vierkantswortel van elk negatief getal schrijven als een veelvoud van i. Beschouw de vierkantswortel van -25.
We kunnen de vierkantswortel van elk negatief getal schrijven als een veelvoud van i. \sqrt{-25}=\sqrt{2525}}(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1))} }=\sqrt{25}\sqrt{-1)(-1)(-1))}(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1)(-1))}).
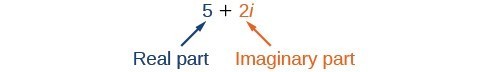
Figuur 1
Een complex getal is de som van een reëel getal en een imaginair getal. Een complex getal wordt in de standaardvorm geschreven als a + bi waarbij a het reële deel is en bi het imaginaire deel. Bijvoorbeeld, 5+2i is een complex getal. Dat is ook het geval met 3+4xqrt{3}i.
Imaginaire getallen onderscheiden zich van reële getallen doordat een kwadraat van een imaginair getal een negatief reëel getal oplevert. Als een positief reëel getal wordt gekwadrateerd, is het resultaat een positief reëel getal en als een negatief reëel getal wordt gekwadrateerd, is het resultaat weer een positief reëel getal. Complexe getallen zijn een combinatie van reële en imaginaire getallen.
Een algemene noot: imaginaire en complexe getallen
Een complex getal is een getal van de vorm a+bi waarbij
- a het reële deel van het complexe getal is.
- bi het imaginaire deel van het complexe getal is.
Als b=0³, dan is a+bi³ een reëel getal. Als a=0 en b is niet gelijk aan 0, dan heet het complex getal een imaginair getal. Een imaginair getal is een even wortel uit een negatief getal.
Hoe: Gegeven een imaginair getal, druk het uit in de standaardvorm.
- Schrijf \sqrt{-a} als \sqrt{a}\sqrt{-1}\.
- Druk \sqrt{-1} uit als i.
- Schrijf \sqrt{a}\cdot i\in de eenvoudigste vorm.
Voorbeeld 1: Een imaginair getal in de standaardvorm uitdrukken
Druk \sqrt{-9} uit in de standaardvorm.
Oplossing
=3i}
In de standaardvorm is dit 0+3i}.
Probeer het 1
Druk \sqrt{-24} uit in standaardvorm.
Oplossing
