Groep

Een groep is een eindige of oneindige verzameling van elementen samen met een binaire operatie (de groepsoperatie genoemd) die samen voldoen aan de vier fundamentele eigenschappen van sluiting, associativiteit, de eigenschap identiteit, en de eigenschap inverse. De operatie waarmee een groep gedefinieerd wordt, wordt vaak de “groepsoperatie” genoemd, en men zegt dat een verzameling een groep is “onder” deze operatie. Elementen , , , … met binaire operatie tussen en aangeduid met vormen een groep als

1. Sluiting: Als en twee elementen zijn in , dan is het product ook in .

2. Associativiteit: De gedefinieerde vermenigvuldiging is associatief, d.w.z. dat voor alle , .

3. Identiteit: Er is een identiteitselement (ook wel 1, , of ) zodanig dat voor elk element .

4. Inverse: Van elk element moet er een inverse (ook wel reciproke) zijn. Daarom bevat de verzameling voor elk element van een element zo dat .

Een groep is een monoïde waarvan elk element inverteerbaar is.

Een groep moet ten minste één element bevatten, waarbij de unieke (tot en met isomorfisme) enkel-elementgroep bekend staat als de triviale groep.

De studie van groepen staat bekend als groepentheorie. Als er een eindig aantal elementen is, heet de groep een eindige groep en het aantal elementen wordt de groepsorde van de groep genoemd. Een deelverzameling van een groep die gesloten is onder de groepsoperatie en de inverse operatie heet een subgroep. Subgroepen zijn ook groepen, en veel veel voorkomende groepen zijn in feite speciale subgroepen van een meer algemene grotere groep.

Een basisvoorbeeld van een eindige groep is de symmetrische groep , dat is de groep van permutaties (of “onder permutatie”) van objecten. De eenvoudigste oneindige groep is de verzameling gehele getallen onder gewone optelling. Voor continue groepen kan men denken aan de reële getallen of aan de verzameling van inverteerbare matrices. Deze laatste twee zijn voorbeelden van Lie-groepen.

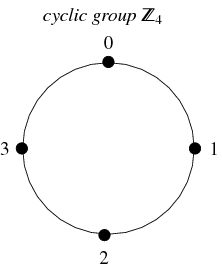
Een zeer algemeen type groep zijn de cyclische groepen. Deze groep is isomorf aan de groep der gehele getallen (modulo ), wordt aangeduid met , , of , en is gedefinieerd voor elk geheel getal . Zij is gesloten onder optelling, associatief, en heeft unieke inverses. De getallen 0 tot en met stellen de elementen voor, waarbij het identiteits-element wordt voorgesteld door 0, en het inverse van wordt voorgesteld door .

Een functie tussen twee groepen die de identiteit en de groepsoperatie behoudt, heet een homomorfisme. Als een homomorfisme een inverse heeft die ook een homomorfisme is, dan heet het een isomorfisme en heten de twee groepen isomorf. Twee groepen die isomorf zijn, worden beschouwd als “hetzelfde” als ze als abstracte groepen worden beschouwd. Bijvoorbeeld, de groep van de rotaties van een vierkant, hieronder afgebeeld, is de cyclische groep .

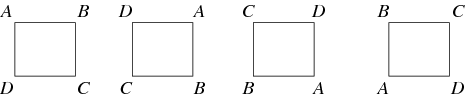
In het algemeen is er sprake van een groepsactie wanneer een groep op een verzameling ingrijpt door de elementen te permuteren, zodat de overdracht van de groep naar de permutatiegroep van de verzameling een homomorfisme is. Bijvoorbeeld, de rotaties van een vierkant zijn een subgroep van de permutaties van de hoeken. Een belangrijke groepsactie voor elke groep is de actie op zichzelf door conjugatie. Dit zijn slechts enkele van de mogelijke groeps-automorfismen. Een andere belangrijke groepsactie is een groepsrepresentatie, waarbij de groep op een vectorruimte inwerkt door inverteerbare lineaire functies. Wanneer het veld van de vectorruimte de complexe getallen zijn, wordt een representatie soms een CG-module genoemd.

Groepsacties, en in het bijzonder representaties, zijn zeer belangrijk in toepassingen, niet alleen in de groepentheorie, maar ook in de natuur- en scheikunde. Aangezien een groep kan worden beschouwd als een abstract wiskundig object, kan eenzelfde groep in verschillende contexten voorkomen. Daarom is het nuttig om een voorstelling van de groep te beschouwen als een bepaalde incarnatie van de groep, die ook andere voorstellingen kan hebben. Een irreducibele representatie van een groep is een representatie waarvoor geen unitaire transformatie bestaat die de representatiematrix in blokdiagonaal zal omzetten. De irreducibele representaties hebben een aantal opmerkelijke eigenschappen, zoals geformaliseerd in de groepsorthogonaliteitstheorem.