Leerdoelen
Aan het eind van dit hoofdstuk zul je in staat zijn:
- Een typisch foto-elektrisch effect experiment te beschrijven.
- De maximale kinetische energie bepalen van foto-elektronen die door fotonen van een bepaalde energie of golflengte worden uitgeworpen, wanneer de maximale kinetische energie van foto-elektronen voor een andere fotonenergie of golflengte wordt gegeven.
Wanneer licht op materialen valt, kan het elektronen uit deze materialen uitwerpen. Dit wordt het foto-elektrisch effect genoemd, wat betekent dat licht (foto) elektriciteit produceert. Een veelgebruikt gebruik van het foto-elektrisch effect is in lichtmeters, zoals die waarmee de automatische iris op verschillende soorten camera’s wordt ingesteld. Op soortgelijke wijze wordt ook gebruik gemaakt van zonnecellen, die u waarschijnlijk in uw rekenmachine hebt of op een dak of een verkeersbord hebt gezien. Deze maken gebruik van het foto-elektrisch effect om licht om te zetten in elektriciteit voor de werking van verschillende apparaten.

Figuur 1. Het foto-elektrisch effect kan worden waargenomen door licht te laten vallen op de metalen plaat in deze vacuümbuis. De door het licht uitgeworpen elektronen worden verzameld op de collectordraad en gemeten als stroom. Een vertragend voltage tussen de collectordraad en de plaat kan dan worden aangepast om de energie van de uitgeworpen elektronen te bepalen. Indien deze bijvoorbeeld voldoende negatief is, zullen geen elektronen de draad bereiken. (credit: P.P. Urone)
Dit effect is al meer dan een eeuw bekend en kan worden bestudeerd met behulp van een apparaat zoals dat in figuur 1 is afgebeeld. Dit cijfer toont een vacuümbuis met een metaalplaat en een collectordraad die door een veranderlijke voltagebron worden verbonden, met de collector negatiever dan de plaat. Wanneer licht (of andere EM-straling) de plaat in de vacuümbuis treft, kunnen er elektronen worden uitgeworpen. Als de elektronen een energie in elektronvolt (eV) hebben die groter is dan het potentiaalverschil in volt tussen de plaat en de draad, zullen sommige elektronen op de draad worden verzameld. Aangezien de elektronenenergie in eV is, waarbij q de elektronlading is en V het potentiaalverschil, kan de elektronenenergie worden gemeten door de vertragende spanning tussen de draad en de plaat aan te passen. De spanning die de elektronen verhindert de draad te bereiken is gelijk aan de energie in eV. Bijvoorbeeld, als -3,00 V de elektronen nauwelijks tegenhoudt, is hun energie 3,00 eV. Het aantal uitgeworpen elektronen kan worden bepaald door de stroom tussen de draad en de plaat te meten. Hoe meer licht, hoe meer elektronen; een beetje schakeling maakt het mogelijk dit apparaat als lichtmeter te gebruiken.
Wat werkelijk belangrijk is aan het foto-elektrisch effect is wat Albert Einstein er uit afleidde. Einstein realiseerde zich dat er verschillende kenmerken van het foto-elektrisch effect waren die alleen verklaard konden worden als EM-straling zelf gekwantiseerd is: de schijnbaar continue stroom van energie in een EM-golf bestaat in feite uit energiequanta, fotonen genaamd. In zijn verklaring van het foto-elektrisch effect definieerde Einstein een gekwantiseerde eenheid of kwantum van EM-energie, dat wij nu een foton noemen, met een energie die evenredig is met de frequentie van de EM-straling. In de vorm van een vergelijking is de fotonenergie E = hf, waarbij E de energie is van een foton met frequentie f en h de constante van Planck. Dit revolutionaire idee lijkt op Planck’s kwantisering van energietoestanden in blackbody oscillatoren, maar het is heel anders. Het is de kwantisering van EM-straling zelf. EM-golven zijn samengesteld uit fotonen en zijn geen continue gladde golven zoals beschreven in eerdere hoofdstukken over optica. Hun energie wordt geabsorbeerd en uitgezonden in brokken, niet continu. Dit is precies in overeenstemming met Planck’s kwantisering van energieniveaus in blackbody oscillatoren, aangezien deze oscillatoren hun energie in stappen van hf verhogen en verlagen door fotonen met E = hf te absorberen en uit te zenden. Wij nemen dit niet met onze ogen waar, omdat er zoveel fotonen in gewone lichtbronnen zitten dat afzonderlijke fotonen onopgemerkt blijven. (Zie figuur 2.) Het volgende deel van de tekst (Fotonenergieën en het elektromagnetisch spectrum) is gewijd aan een bespreking van fotonen en enkele van hun eigenschappen en implicaties. Voorlopig zullen we het fotonenconcept gebruiken om het foto-elektrisch effect uit te leggen, ongeveer zoals Einstein deed.
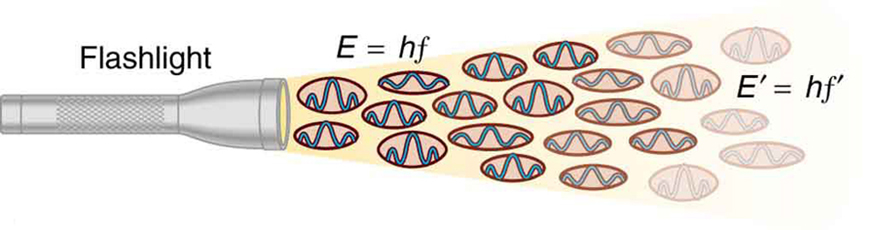
Figuur 2. Een EM-golf met frequentie f is opgebouwd uit fotonen, of individuele kwanta van EM-straling. De energie van elk foton is E = hf, waarbij h de constante van Planck is en f de frequentie van de EM-straling. Een hogere intensiteit betekent meer fotonen per oppervlakte-eenheid. De zaklamp zendt grote aantallen fotonen uit van veel verschillende frequenties, vandaar dat anderen energie E′ = hf′ hebben, enzovoort.
Het foto-elektrisch effect heeft de hieronder besproken eigenschappen. Al deze eigenschappen zijn consistent met het idee dat individuele fotonen van EM-straling worden geabsorbeerd door individuele elektronen in een materiaal, waarbij het elektron de energie van het foton wint. Sommige van deze eigenschappen zijn niet in overeenstemming met het idee dat EM-straling een eenvoudige golf is. Laten we voor het gemak eens kijken wat er gebeurt met monochromatische EM-straling waarin alle fotonen dezelfde energie hf hebben.
- Als we de frequentie van de EM-straling die op een materiaal valt variëren, vinden we het volgende: Voor een gegeven materiaal is er een drempelfrequentie f0 voor de EM-straling, waaronder geen elektronen worden uitgeworpen, ongeacht de intensiteit. Individuele fotonen hebben interactie met individuele elektronen. Dus als de fotonenergie te klein is om een elektron af te breken, zullen er geen elektronen worden uitgeworpen. Als EM-straling een eenvoudige golf was, zou voldoende energie kunnen worden verkregen door de intensiteit te verhogen.
- Zodra EM-straling op een materiaal valt, worden elektronen zonder vertraging uitgeworpen. Zodra een individueel foton van een voldoende hoge frequentie door een individueel elektron wordt geabsorbeerd, wordt het elektron uitgeworpen. Indien de EM-straling een eenvoudige golf zou zijn, zouden verscheidene minuten nodig zijn om voldoende energie op het metaaloppervlak te deponeren om een elektron uit te werpen.
- Het aantal uitgeworpen elektronen per tijdseenheid is evenredig met de intensiteit van de EM-straling en met geen ander kenmerk. EM-straling van hoge intensiteit bestaat uit grote aantallen fotonen per oppervlakte-eenheid, waarbij alle fotonen dezelfde karakteristieke energie hf hebben.
- Als we de intensiteit van de EM-straling variëren en de energie van de uitgeworpen elektronen meten, vinden we het volgende: De maximale kinetische energie van uitgeworpen elektronen is onafhankelijk van de intensiteit van de EM-straling. Aangezien er zoveel elektronen in een materiaal zijn, is het uiterst onwaarschijnlijk dat twee fotonen tegelijkertijd met hetzelfde elektron in wisselwerking treden, waardoor de gegeven energie toeneemt. In plaats daarvan (zoals opgemerkt in 3 hierboven) resulteert een verhoogde intensiteit in meer elektronen van dezelfde energie die worden uitgeworpen. Als EM-straling een eenvoudige golf zou zijn, zou een hogere intensiteit meer energie kunnen geven, en zouden elektronen met een hogere energie worden uitgeworpen.
- De kinetische energie van een uitgeworpen elektron is gelijk aan de fotonenergie min de bindingsenergie van het elektron in het specifieke materiaal. Een individueel foton kan al zijn energie aan een elektron afgeven. De energie van het foton wordt gedeeltelijk gebruikt om het elektron los te breken van het materiaal. De rest gaat in de kinetische energie van het uitgeworpen elektron. In vergelijking wordt dit gegeven door KEe = hf – BE, waarbij KEe de maximale kinetische energie van het uitgeworpen elektron is, hf de energie van het foton, en BE de bindingsenergie van het elektron met het materiaal in kwestie. (BE wordt ook wel de werkfunctie van het materiaal genoemd.) Deze vergelijking, die in 1905 door Einstein werd opgesteld, verklaart de eigenschappen van het foto-elektrisch effect op kwantitatieve wijze. Een individueel foton van EM-straling (het komt niet op een andere manier) heeft een wisselwerking met een individueel elektron, waarbij voldoende energie, BE, wordt toegevoerd om het te breken, waarbij de rest naar kinetische energie gaat. De bindingsenergie is BE = hf0, waarbij f0 de drempelfrequentie is voor het materiaal in kwestie. Figuur 3 toont een grafiek van de maximale KEe tegen de frequentie van de invallende EM-straling die op een bepaald materiaal valt.
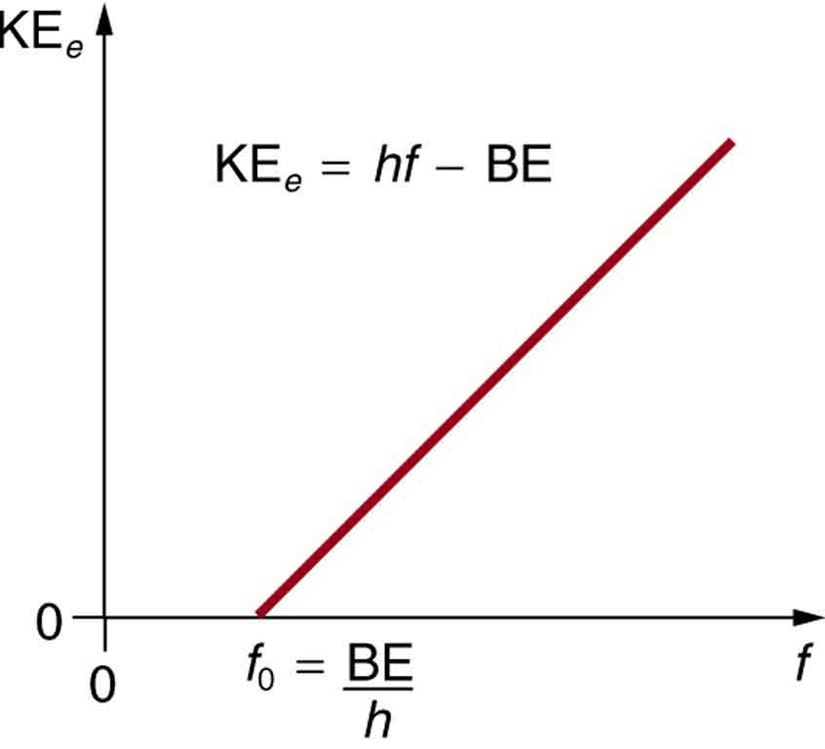
Figuur 3. Foto-elektrisch effect. Een grafiek van de kinetische energie van een uitgeworpen elektron, KEe, afgezet tegen de frequentie van de op een bepaald materiaal inwerkende EM-straling. Er is een drempelfrequentie waaronder geen elektronen worden uitgeworpen, omdat het individuele foton dat in wisselwerking staat met een individueel elektron onvoldoende energie heeft om het weg te breken. Boven de drempelwaarde neemt KEe lineair toe met f, in overeenstemming met KEe = hf – BE. De helling van deze lijn is h – de gegevens kunnen worden gebruikt om de constante van Planck experimenteel te bepalen. Einstein gaf de eerste succesvolle verklaring van dergelijke gegevens door het idee van fotonen voor te stellen – quanta van EM straling.
Einstein’s idee dat EM straling gekwantiseerd is, was cruciaal voor het begin van de quantum mechanica. Het is een veel algemener concept dan zijn verklaring van het foto-elektrisch effect zou kunnen impliceren. Alle EM-straling kan ook worden gemodelleerd in de vorm van fotonen, en de eigenschappen van EM-straling zijn volledig in overeenstemming met dit feit. (Zoals we in het volgende hoofdstuk zullen zien, kunnen veel aspecten van EM-straling, zoals de gevaren van ultraviolette (UV) straling, alleen worden verklaard door fotoneigenschappen). Einstein, die vooral bekend is om zijn moderne relativiteit, legde een belangrijke kiem voor de kwantummechanica in 1905, in hetzelfde jaar dat hij zijn eerste artikel over de speciale relativiteit publiceerde. Zijn verklaring van het foto-elektrisch effect vormde de basis voor de Nobelprijs die hem in 1921 werd toegekend. Hoewel zijn andere bijdragen aan de theoretische natuurkunde ook in die prijs werden vermeld, werden de speciale en algemene relativiteit niet volledig erkend, ondanks het feit dat zij in 1921 gedeeltelijk door experimenten waren geverifieerd. Hoewel hij als held werd aanbeden, heeft deze grote man nooit Nobel erkenning gekregen voor zijn beroemdste werk – de relativiteit.
Voorbeeld 1. Berekening van fotonenergie en het foto-elektrisch effect: Een Violet Licht
1. Wat is de energie in joules en elektronvolts van een foton van 420-nm violet licht?
2. Wat is de maximale kinetische energie van elektronen die door 420-nm violet licht uit calcium worden geworpen, gegeven dat de bindingsenergie (of werkfunctie) van elektronen voor calciummetaal 2,71 eV is?
Strategie
Om deel 1 op te lossen, moet u opmerken dat de energie van een foton gegeven wordt door E = hf. Voor deel 2 is het, zodra de energie van het foton is berekend, een eenvoudige toepassing van KEe = hf – BE om de maximale kinetische energie van het uitgeworpen elektron te vinden, aangezien BE gegeven is.
Oplossing voor deel 1
De energie van een foton wordt gegeven door E = hf.
Omdat we de golflengte hebben en niet de frequentie, lossen we voor de frequentie de bekende relatie c = fλ op, die oplevert f=\frac{c}{\lambda}}.
Combinatie van deze twee vergelijkingen geeft de nuttige relatie E=\frac{hc}{\lambda}}.
Vervanging van de bekende waarden levert nu op
E= E= E = E = E = E = E = E = E = E = E = E = E = E = E = E = E = E = E = E.00times10^{8}}(m/s)}{420}times10^{-9}{ m}}=4.74}times10^{-19}(J})
Omgerekend naar eV is de energie van het foton
Displaystyle{E}=(4.47 maal10^{-19} J}}(4…47 maal10^{-19} J}}(1,6 maal10^{-19} J}}=2,96)
Oplossing voor deel 2
De kinetische energie van het uitgeworpen elektron is nu een eenvoudige toepassing van de vergelijking KEe = hf – BE. Invullen van de fotonenergie en de bindingsenergie levert KEe = hf – BE = 2.96 eV – 2.71 eV = 0.246 eV.
Discussie
De energie van dit 420-nm foton van violet licht is een minuscule fractie van een joule, en dus is het geen wonder dat een enkel foton voor ons moeilijk direct waar te nemen is – mensen zijn meer ingesteld op energieën in de orde van joules. Maar als we kijken naar de energie in elektronvolt, kunnen we zien dat dit foton genoeg energie heeft om atomen en moleculen te beïnvloeden. Een DNA-molecuul kan bijvoorbeeld worden gebroken met een energie van ongeveer 1 eV, en typische atomaire en moleculaire energieën liggen in de orde van eV, zodat het UV-foton in dit voorbeeld biologische effecten kan hebben. Het uitgeworpen elektron (foto-elektron genoemd) heeft een vrij lage energie, en het zou niet ver reizen, behalve in een vacuüm. Het elektron zou worden tegengehouden door een vertragend potentiaal van slechts 0,26 eV. In feite, als de golflengte van het foton langer was en zijn energie minder dan 2,71 eV, dan zou de formule een negatieve kinetische energie geven, een onmogelijkheid. Dit betekent eenvoudigweg dat de 420-nm fotonen met hun 2,96-eV energie niet veel boven de frequentiedrempel komen. U kunt zelf aantonen dat de drempelgolflengte 459 nm is (blauw licht). Dit betekent dat als calciummetaal wordt gebruikt in een lichtmeter, de meter ongevoelig zal zijn voor golflengten langer dan die van blauw licht. Zo’n lichtmeter zou bijvoorbeeld volledig ongevoelig zijn voor rood licht.
PhET Explorations: Photoelectric Effect
Zie hoe licht elektronen van een metalen object wegslaat, en speel het experiment na dat aan de wieg stond van de kwantummechanica.

Klik om de simulatie te downloaden. Uitvoeren met Java.
Samenvatting
- Het foto-elektrisch effect is het proces waarbij EM-straling elektronen uit een materiaal werpt.
- Einstein stelde voor dat fotonen quanta van EM-straling zijn met energie E = hf, waarbij f de frequentie van de straling is.
- Alle EM-straling is opgebouwd uit fotonen. Zoals Einstein verklaarde, zijn alle kenmerken van het foto-elektrisch effect het gevolg van de wisselwerking van individuele fotonen met individuele elektronen.
- De maximale kinetische energie KEe van uitgeworpen elektronen (foto-elektronen) wordt gegeven door KEe = hf – BE, waarbij hf de fotonenergie is en BE de bindingsenergie (of werkfunctie) van het elektron aan het specifieke materiaal.
Conceptuele vragen
- Is zichtbaar licht de enige soort EM-straling die het foto-elektrisch effect kan veroorzaken?
- Welke aspecten van het foto-elektrisch effect kunnen niet verklaard worden zonder fotonen? Welke kunnen worden verklaard zonder fotonen? Zijn deze laatste inconsistent met het bestaan van fotonen?
- Is het foto-elektrisch effect een direct gevolg van het golfkarakter van EM-straling of van het deeltjeskarakter van EM-straling? Leg kort uit.
- Insulatoren (niet-metalen) hebben een hogere BE dan metalen, en het is moeilijker voor fotonen om elektronen uit te werpen uit insulatoren. Bespreek hoe dit verband houdt met de vrije ladingen in metalen die hen tot goede geleiders maken.
- Als je een stuk metaal oppakt en schudt dat elektronen bevat die vrij als stroom kunnen bewegen, vallen er geen elektronen uit. Maar als je het metaal verhit, kunnen elektronen worden weggekookt. Leg deze beide feiten uit in verband met de hoeveelheid en de verdeling van de energie die gemoeid is met het schudden van het voorwerp in vergelijking met het verwarmen ervan.
Problemen &Oefeningen
- Wat is de langste golflengte van EM-straling die een foto-elektron uit zilver kan uitwerpen, gegeven dat de bindingsenergie 4.73 eV is? Is dit in het zichtbare gebied?
- Vind het foton met de langste golflengte dat een elektron kan wegstoten uit kalium, gegeven dat de bindingsenergie 2.24 eV is. Is dit zichtbare EM-straling?
- Wat is de bindingsenergie in eV van elektronen in magnesium, als het foton met de langste golflengte dat elektronen kan uitwerpen 337 nm bedraagt?
- Bereken de bindingsenergie in eV van elektronen in aluminium, als het foton met de langste golflengte dat elektronen kan uitwerpen 304 nm bedraagt.
- Wat is de maximale kinetische energie in eV van elektronen die door EM-straling van 450 nm uit natriummetaal worden weggeslingerd, gegeven dat de bindingsenergie 2,28 eV bedraagt?
- UV-straling met een golflengte van 120 nm valt op goudmetaal, waaraan elektronen met 4,82 eV zijn gebonden. Wat is de maximale kinetische energie van de uitgeworpen foto-elektronen?
- Violet licht met een golflengte van 400 nm werpt elektronen met een maximale kinetische energie van 0,860 eV uit natriummetaal. Wat is de bindingsenergie van elektronen aan natriummetaal?
- UV-straling met een golflengte van 300 nm valt op uraniummetaal en werpt elektronen met een kinetische energie van 0,500 eV uit. Wat is de bindingsenergie van elektronen aan uraniummetaal?
- (a) Wat is de golflengte van de EM-straling die elektronen van 2,00 eV uit calciummetaal werpt, gegeven dat de bindingsenergie 2,71 eV is? (b) Welk type EM-straling is dit?
- Vind de golflengte van fotonen die elektronen van 0,100 eV uit kalium wegstoten, gegeven dat de bindingsenergie 2,24 eV is. Zijn deze fotonen zichtbaar?
- Wat is de maximale snelheid van de elektronen die door 80-nm fotonen uit een materiaal worden uitgeworpen, als ze met 4,73 eV aan het materiaal zijn gebonden?
- Foto-elektronen uit een materiaal met een bindingsenergie van 2,71 eV worden uitgeworpen door 420-nm fotonen. Hoe lang doen deze elektronen er over om, eenmaal uitgeworpen, 2,50 cm af te leggen naar een detectieapparaat?
- Een laser met een vermogen van 2,00 mW bij een golflengte van 400 nm wordt geprojecteerd op calciummetaal. (a) Hoeveel elektronen worden per seconde uitgeworpen? (b) Welk vermogen wordt door de elektronen afgevoerd, gegeven dat de bindingsenergie 2,71 eV bedraagt?
- (a) Bereken het aantal foto-elektronen per seconde dat wordt weggeslingerd uit een oppervlak van 1,00 mm2 natriummetaal door elektromagnetische straling van 500 nm met een intensiteit van 1,30 kW/m2 (de intensiteit van zonlicht boven de dampkring van de aarde). (b) Gegeven dat de bindingsenergie 2,28 eV is, welk vermogen wordt door de elektronen afgevoerd? (c) De elektronen nemen minder vermogen mee dan door de fotonen wordt toegevoerd. Waar gaat het andere vermogen heen? Hoe kan het worden teruggewonnen?
- Onredelijke resultaten. Rood licht met een golflengte van 700 nm wordt geprojecteerd op magnesiummetaal waaraan elektronen zijn gebonden met 3,68 eV. (a) Bereken met KEe = hf – BE de kinetische energie van de weggeslingerde elektronen. (b) Wat is er onredelijk aan dit resultaat? (c) Welke aannames zijn onredelijk of inconsistent?
- Onredelijke resultaten. (a) Wat is de bindingsenergie van elektronen aan een materiaal waaruit 4,00-eV elektronen worden uitgeworpen door 400-nm EM-straling? (b) Wat is er onredelijk aan dit resultaat? (c) Welke aannames zijn onredelijk of inconsistent?
Glossary
photoelectric effect: het verschijnsel waarbij sommige materialen elektronen uitwerpen wanneer er licht op wordt geschenen
photon: een kwantum, of deeltje, van elektromagnetische straling
photon energy: de hoeveelheid energie die een foton heeft; E = hf
bindingsenergie: ook wel de werkfunctie genoemd; de hoeveelheid energie die nodig is om een elektron uit een materiaal te werpen
Selected Solutions to Problems & Exercises
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm; (b) Ultraviolet
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) negatieve kinetische energie; (c) dat de elektronen zouden worden vrijgeslagen.
