Het fasediagram van water
Figuur 11.23 “Twee versies van het fasediagram van water” toont het fasediagram van water en illustreert dat het tripelpunt van water optreedt bij 0,01°C en 0,00604 atm (4,59 mmHg). Het drievoudig punt (273,16 K), dat veel reproduceerbaarder is dan het smeltpunt van ijs, dat afhangt van de hoeveelheid opgeloste lucht en de atmosferische druk, wordt gebruikt om de absolute (Kelvin) temperatuurschaal te definiëren. Het tripelpunt vertegenwoordigt ook de laagste druk waarbij een vloeibare fase in evenwicht kan bestaan met de vaste stof of damp. Bij drukken lager dan 0,00604 atm smelt ijs dus niet tot een vloeistof als de temperatuur stijgt; de vaste stof sublimeert direct tot waterdamp. Sublimatie van water bij lage temperatuur en druk kan worden gebruikt om voedingsmiddelen en dranken te “vriesdrogen”. Het voedsel of de drank wordt eerst afgekoeld tot temperaturen onder nul en in een vat geplaatst waarin de druk lager wordt gehouden dan 0,00604 atm. Vervolgens, als de temperatuur wordt verhoogd, sublimeert het water, waardoor het gedehydrateerde voedsel (zoals dat wordt gebruikt door backpackers of astronauten) of de poedervormige drank (zoals bij gevriesdroogde koffie) overblijft.
Het fasediagram voor water, afgebeeld in deel (b) in figuur 11.23 “Twee versies van het fasediagram van water”, toont de grens tussen ijs en water op een vergrote schaal. De smeltcurve van ijs loopt omhoog en iets naar links in plaats van omhoog en naar rechts zoals in figuur 11.22 “Een typisch fasediagram voor een stof met drie fasen – vast, vloeibaar en gas – en een superkritisch gebied”; dat wil zeggen dat het smeltpunt van ijs daalt met toenemende druk; bij 100 MPa (987 atm) smelt ijs bij -9°C. Water gedraagt zich zo omdat het een van de weinige stoffen is waarvan bekend is dat de kristallijne vaste stof minder dicht is dan de vloeistof (andere stoffen zijn antimoon en bismut). Het verhogen van de druk van ijs dat in evenwicht is met water bij 0°C en 1 atm heeft de neiging sommige moleculen dichter bij elkaar te duwen, waardoor het volume van het monster afneemt. De volumevermindering (en overeenkomstige toename in dichtheid) is kleiner voor een vaste stof of een vloeistof dan voor een gas, maar ze is voldoende om een deel van het ijs te doen smelten.
Figuur 11.23 Twee versies van het fasediagram van water
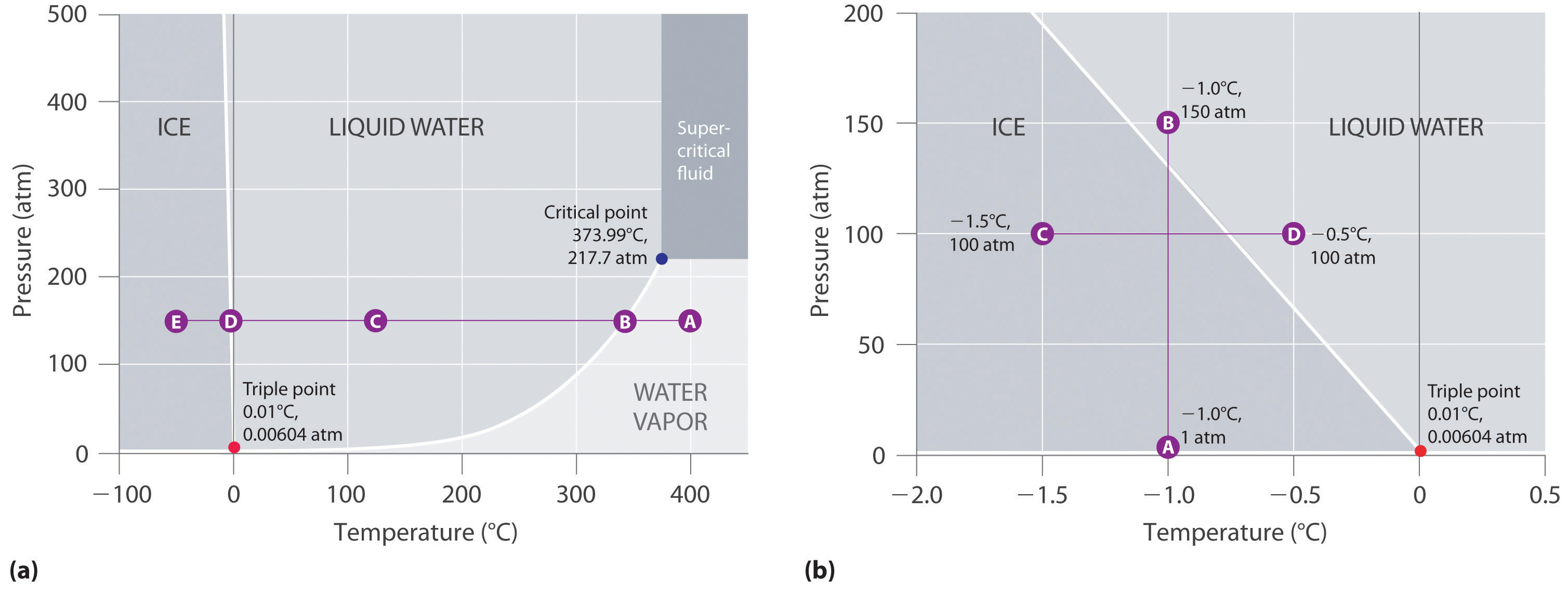
(a) In deze grafiek met lineaire temperatuur- en drukassen is de grens tussen ijs en vloeibaar water bijna verticaal. (b) Deze grafiek met een uitgebreide schaal illustreert de daling van het smeltpunt bij toenemende druk. (De letters verwijzen naar punten die in voorbeeld 10 zijn besproken.)
In deel b) in figuur 11.23 “Twee versies van het fasediagram van water” bevindt punt A zich bij P = 1 atm en T = -1,0°C, binnen het vaste (ijs) gebied van het fasediagram. Als de druk toeneemt tot 150 atm terwijl de temperatuur gelijk blijft, gaat de lijn van punt A over de grens tussen ijs en water naar punt B, dat in het gebied van vloeibaar water ligt. Bijgevolg zal bij toepassing van een druk van 150 atm het ijs smelten bij -1,0°C. We hebben reeds aangegeven dat de drukafhankelijkheid van het smeltpunt van water van vitaal belang is. Als de vast-vloeibaar grens in het fasediagram van water naar boven en naar rechts zou hellen in plaats van naar links, zou ijs dichter zijn dan water, zouden ijsblokjes zinken, zouden waterleidingen niet barsten als ze bevriezen en zou antivries in automotoren overbodig zijn.
Tot voor kort werd in veel handboeken beschreven dat schaatsen mogelijk is omdat de druk die door de schaats van de schaatser wordt opgewekt hoog genoeg is om het ijs onder de schaats te smelten, waardoor een smerende laag van vloeibaar water ontstaat die de schaats in staat stelt over het ijs te glijden. Hoewel deze verklaring intuïtief bevredigend is, is zij onjuist, zoals we met een eenvoudige berekening kunnen aantonen. Herinner u uit hoofdstuk 10 “Gassen” dat druk (P) de uitgeoefende kracht (F) per oppervlakte-eenheid (A) is:
Vergelijking 11.4
P = F A
Om de druk te berekenen die een schaatser op het ijs uitoefent, hoeven we alleen de uitgeoefende kracht en de oppervlakte van het schaatsijzer te berekenen. Als we uitgaan van een schaatser van 75,0 kg, dan is de kracht die de schaatser als gevolg van de zwaartekracht op het ijs uitoefent
Vergelijking 11.5
F = mg
waarbij m de massa is en g de versnelling als gevolg van de zwaartekracht van de aarde (9,81 m/s2). De kracht is dus
Vergelijking 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Als we aannemen dat de schaatsbladen 2.0 mm breed en 25 cm lang zijn, dan is de oppervlakte van de onderkant van elk blad
Vergelijking 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Als de schaatser op één voet glijdt, is de druk die op het ijs wordt uitgeoefend
Vergelijking 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
De druk is veel lager dan de druk die nodig is om het smeltpunt van ijs ook maar met 1°C te verlagen, en de ervaring leert dat het mogelijk is om te schaatsen zelfs wanneer de temperatuur ver onder het vriespunt ligt. Het door druk veroorzaakte smelten van het ijs kan dus niet de lage wrijving verklaren die schaatsers (en ijshockey pucks) in staat stelt te glijden. Recent onderzoek wijst uit dat het oppervlak van ijs, waar de geordende reeks watermoleculen de lucht ontmoet, bestaat uit een of meer lagen bijna vloeibaar water. Deze lagen, samen met het smelten door wrijving als een schaatser zich voortbeweegt, lijken een verklaring te geven voor zowel het gemak waarmee een schaatser glijdt als het feit dat schaatsen moeilijker wordt onder ongeveer -7°C, wanneer het aantal smerende waterlagen aan het oppervlak afneemt.
