一定加速度
2次元の発射体の運動は、水平軸と垂直軸に沿った運動の2つに分けて分析する。
学習目標
水平軸と垂直軸に沿った2次元の投射運動を分析する
キーポイント
キーポイント
- 2次元での運動における一定の加速度は一般的に投射パターンに従っています。
- 投射運動とは、重力による(垂直)加速度だけを受ける、空中に投げられたり投影されたりする物体の運動です。
- 私たちは、2次元投射運動を垂直軸と水平軸に沿って2つの独立した1次元運動に分割して分析します。
主要用語
- kinematic:運動または運動学に関するもの
投射運動とは、重力のみを受けて空中に投げられる、または投射されるオブジェクトの運動である。 この物体を投射物と呼び、その軌道を軌跡と呼ぶ。 物体の落下運動は、水平方向の移動がない単純な一次元の投射運動である。 サッカーボールなどの投擲物のような2次元の投射運動では、運動には垂直方向と水平方向の両方の成分がある。
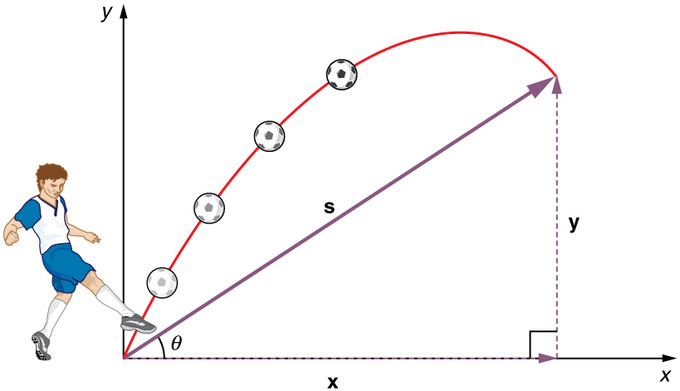
投射運動。
覚えておくべき最も重要な事実は、垂直軸に沿った運動は独立しており、したがって別々に分析することができることである。 2次元の投射運動を解析する鍵は、水平軸に沿った運動と垂直軸に沿った運動の2つに分けることである。 運動を記述するためには、変位と同様に速度と加速度を扱わなければならない。
ここでは重力以外の力(例えば空気抵抗や摩擦など)は無視できると仮定する。 そうすると、加速度の成分は非常に単純になる。 \text{a}_text{y} = -thext{g} = -9.81 \frac{thext{m}}{text{s}^2} (ここでは重力による加速度が一定となるように、運動は地表近くの十分小さい高さで起こるものとします). 重力加速度は鉛直方向だけであるから、 \text{a}_text{x} = 0 となる。従って、(1)と(2)の運動方程式はそれぞれ、
text{x} = \text{x}_0 + \text{v}_text{x} で表される。 \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
Text{v}_text{y}^2=Text{v}_{0text{y}}^2+2}text{a}_text{y}(\text{y}-they}_0) 2次元射手運動を縦と横軸の独立した1次元運動2つに分けて解析してみる。 水平方向の運動は単純である。なぜなら “text{a}_text{x}”=0であり、”text{v}_text{x}”は一定であるからである。 垂直方向の速度は物体が上昇するにつれて減少し始め、最も高い位置で垂直方向の速度は0となる。 物体が再び地球に向かって落下すると、鉛直方向の速度は再び大きくなるが、最初の鉛直方向の速度とは反対の方向を向く。 このとき、軌跡上の任意の点での全速度を得るために、ⒶとⒷの運動を組み合わせることができる。
