Tycho BraheEdit

ティコ・ブラーエの地軸モデル
Tycho Brahe (1546-1601) はデンマーク貴族で、当時天文学者としてよく知られていた人物である。 宇宙の理解をさらに進めるには、ニコラウス・コペルニクスが頼った観測よりも新しい、より正確な観測が必要であり、ティコはこの分野で大きな前進を遂げました。 ティコは、太陽が地球の周りを回り、惑星が太陽の周りを回るという地動説(ティコ系)を打ち出しました。 ティコはコペルニクスの体系の長所を評価していましたが、他の多くの人々と同様に、地球の動きを受け入れることができませんでした
1572年、ティコ・ブラーエはカシオペア座に新しい星を観測します。 その星は18ヶ月間、視差もなく明るく輝き、アリストテレスのモデルによる星の天域の一部であることがわかりました。 しかし、このモデルでは、天界に変化が起こることはありえないので、ティコの観測はアリストテレスの理論を大きく否定するものであった。 1577年、ティコは天空に大きな彗星を観測した。 視差の観測から、彗星は惑星の領域を通過していることがわかった。 アリストテレスの理論では、この領域は固体球面上の一様な円運動しか存在せず、彗星がこの領域に入ることは不可能であった。 ティコは、このような球体は存在しないと結論づけ、惑星の軌道を維持するものは何かという問題を提起した
デンマーク国王の後援を得て、ティコ・ブラーエはフヴェンにウラニボーグという天文台を設立した。 20年にわたり、ティコと彼の天文学者チームは、それまでよりもはるかに正確な天体観測を行った。 これらの観測結果は、将来の天文学の飛躍的進歩に不可欠なものとなる。
ヨハネス・ケプラー編集部

ケプラーはティコ・ブラーエのアシスタントとして就職し、ブラーエの不意の死により皇帝ルドルフ2世の帝国数学者として彼に代わることになった。 そして、ブラーエの膨大な観測データをもとに、惑星運動の三法則など、天文学の分野で目覚ましい進歩を遂げることができたのである。 ケプラーはティコの観測によって、惑星が楕円を描いて運動すること、太陽は軌道の中心に直接座っているのではなく、焦点に座っていることを証明することができたからである。 ケプラーの後に登場したガリレオ・ガリレイは、十分な倍率の望遠鏡を独自に開発し、金星を研究して月のような満ち欠けがあることを発見した。 金星の満ち欠けの発見は、地動説から天動説に移行した理由の一つとして、より大きな影響を与えた。 アイザック・ニュートンの『プリンキピア・マテマティカ』はコペルニクス的転回を完結させた。 1596年、ケプラーは最初の著書『宇宙論的神秘』(Mysterium Cosmographicum)を出版しました。これは、天文学者がコペルニクス的宇宙論を支持するのは1540年以来、トーマス・ディッジス(Thomas Digges, 1576年)に次いで2番目でした。 この本は、ピタゴラス数理と5つのプラトン立体を用いて、惑星の数、比率、順序を説明する彼のモデルを記述したものであった。 この本は、ティコ・ブラーエの尊敬を集め、ケプラーをプラハに招き、彼の助手を務めることになりました。
1600年、ケプラーは、当時知られていた6つの惑星のうち、2番目に偏心した火星の軌道に着手します。 この研究は、1609年に出版された彼の次の著書「新星天文学」の基礎となった。 この本は、惑星の軌道をエピシクルで修正した円ではなく、天動説と楕円を主張したものである。 この本には、彼の名を冠した惑星運動の三法則のうち、最初の2つが含まれている。 1619年、ケプラーは、単惑星の運動ではなく、2つの惑星の関係を示した3つ目の法則と最後の法則を発表した
ケプラーの天文学の仕事は、新しい部分もあった。 ケプラーの天文学の研究は、新しい部分もあった。彼は、先達とは異なり、惑星が一様な円運動をするという仮定を捨て、楕円運動に置き換えた。 また、コペルニクスのように、地動説ではなく天動説の物理的実在性を主張した。
ケプラーの惑星運動の法則編集
1.楕円の法則。 すべての惑星は太陽を1つの焦点として楕円の軌道を描いて動く。 2. 2.等面積等時間の法則:惑星と太陽を結ぶ線は、等しい時間に等しい面積を掃引する。 3. 調和の法則。 惑星が太陽の周りを回るのに必要な時間(周期と呼ぶ)は、楕円の長軸の3/2乗に比例する。 比例定数はすべての惑星で同じである。
ガリレオ・ガリレイ編集部
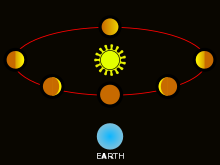
1610年にガリレオが観測した金星の位相
Galileo Galileiはイタリアの科学者で、「近代観測天文学の父」と呼ばれることがあります。 望遠鏡の改良、天体観測、コペルニクス理論の支持など、すべてがコペルニクス革命に不可欠なものであった。 この新しい装置を使って、ガリレオは数々の天体観測を行い、1610年に『Sidereus Nuncius』として出版した。 この本の中で彼は、月の表面は粗く、凹凸があり、不完全であると述べている。 また、「明るい部分と暗い部分を分ける境界線は、完全な球形の固体で起こるような均一な楕円形の線ではなく、図が示すように、不均一で荒く、非常にしなやかな線によって示されている」とも述べている。 これらの観測は、月は完全な球体であるというアリストテレスの主張と、天は完全で不変であるという大きな考え方に挑戦するものであった。 数日間に渡って木星を観測していた彼は、木星の近くにある4つの星の位置が、恒星であればありえないほど変化していることに気づいたのである。 その結果、この4つの星は木星の周りを回っていて、実は星ではなく月であると結論づけた。 アリストテレスの宇宙論では、すべての天体は地球の周りを回っているとされており、月がある惑星は明らかにその通念に反するものであったため、これは画期的な発見であった。 1610年、ガリレオは金星に、地球から観察できる月の満ち欠けと同じような満ち欠けがあることを発見した。 これは、金星が太陽の周りを公転しているため、すべての満ち欠けが見えるとするコペルニクス説やティコウス説と、一部の満ち欠けしか見えないとする天動説とで説明できるものであった。 ガリレオの金星観測により、プトレマイオスの方式は大いに疑われ、その後、主要な天文学者の大半が様々な天動説に転換していったため、彼の発見は地動説から天動説への移行において最も影響力のあるものの1つとなった。
恒星の球編集
16世紀、コペルニクスに影響を受けたトマス・ディッジ、ジョルダーノ・ブルーノ、ウィリアム・ギルバートなど多くの作家が、他の星を遠い太陽として、無限に広がる宇宙、さらには無限の宇宙を主張しました。 これは、アリストテレスが主張した恒星の球体という考え方とは対照的である。 コペルニクスやケプラーは反対したが(ガリレオは意見を述べなかった)、17世紀半ばには、ルネ・デカルトの支持もあって、広く受け入れられるようになった。 アイザック・ニュートン

Newton is known England physicist and mathematian who known for his book Philosophiæ Naturalis Principia Mathematica. 運動と万有引力の法則を発表し、科学革命の中心的人物となった。 ニュートンの法則は、コペルニクス革命の終着点ともいわれる
ニュートンは、ケプラーの惑星運動の法則を利用して万有引力の法則を導き出した。 ニュートンの万有引力の法則は、彼が開発し、著書『プリンキピア』で提案した最初の法則である。 この法則は、どんな2つの物体も互いに引力を及ぼし合うというものである。 その力の大きさは、物体の重力質量の積に比例し、両者の距離の二乗に反比例する。 ニュートンの万有引力の法則とともに、『プリンキピア』は運動の三法則も提示している。 この三法則は、物体に正味の力が加わったときの慣性、加速度、作用、反作用を説明する。
Immanuel KantEdit
Immanuel Kantは『純粋理性批判』(1787版)で「コペルニクス革命」と彼の新しい超越的哲学の認識論に平行を引き、「超越的な哲学の認識論」は、「純粋理性革命」と「純粋理性批判」の間にある。 この比較は、『純粋理性批判』第2版(1787年刊行、1781年の初版を大幅に改訂)の序文でなされている。 カントは、コペルニクスが、静止した観衆のまわりを天体が回っているという仮定から、動く観衆を仮定するように、形而上学も、「まさにコペルニクスの第一仮説の線上に進んで」、「知識が対象に適合しなければならない」という仮定から、「対象が我々の知識に適合しなければならない」という仮定に移行すべきだと主張するのである。
カントが自分の哲学を「コペルニクスの第一仮説の線上に正確に進行する」と言った意味については、これまで多くのことが語られてきた。 カントの類推の妥当性については、ほとんどの論者が、カントはコペルニクスの第一の動きを反転させたと見ているため、長年の議論がある。 トム・ロックモアによれば、カント自身は「コペルニクス的革命」という言葉を自分について使ったことはなかったが、他の人々によって彼の作品に「日常的に」適用されていたということである
。
