Accélération constante
Analyser un mouvement de projectile en deux dimensions se fait en le décomposant en deux mouvements : le long des axes horizontal et vertical.
Objectifs d’apprentissage
Analyser un mouvement de projectile bidimensionnel le long des axes horizontal et vertical
Principaux enseignements
Points clés
- L’accélération constante dans un mouvement en deux dimensions suit généralement un modèle de projectile.
- Le mouvement de projectile est le mouvement d’un objet lancé ou projeté dans l’air, soumis uniquement à l’accélération (verticale) due à la gravité.
- Nous analysons le mouvement de projectile bidimensionnel en le décomposant en deux mouvements unidimensionnels indépendants le long des axes vertical et horizontal.
Termes clés
- cinématique : de ou relatif au mouvement ou à la cinématique
Le mouvement de projectile est le mouvement d’un objet lancé, ou projeté, dans l’air, soumis uniquement à la force de gravité. L’objet est appelé projectile, et son trajet est appelé trajectoire. Le mouvement des objets qui tombent est un type unidimensionnel simple de mouvement de projectile dans lequel il n’y a pas de mouvement horizontal. Dans un mouvement de projectile bidimensionnel, comme celui d’un ballon de football ou d’un autre objet lancé, il y a à la fois une composante verticale et une composante horizontale au mouvement.
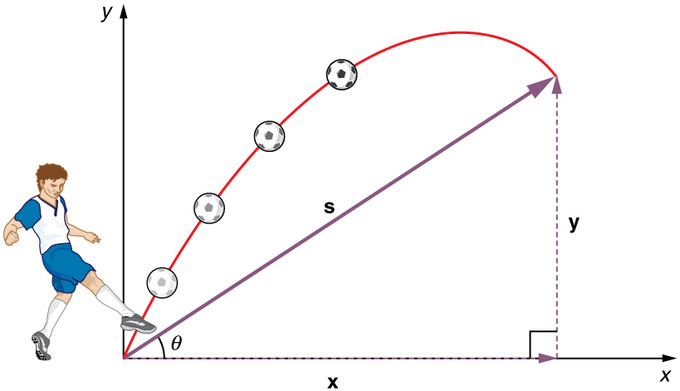
Mouvement de projectile : Lancer une pierre ou donner un coup de pied à un ballon produit généralement un modèle de mouvement de projectile qui a une composante verticale et une composante horizontale.
Le fait le plus important à retenir est que le mouvement le long d’axes perpendiculaires est indépendant et peut donc être analysé séparément. La clé pour analyser le mouvement d’un projectile à deux dimensions est de le décomposer en deux mouvements, l’un le long de l’axe horizontal et l’autre le long de l’axe vertical. Pour décrire le mouvement, nous devons traiter la vitesse et l’accélération, ainsi que le déplacement.
Nous supposerons que toutes les forces, à l’exception de la gravité (comme la résistance de l’air et la friction, par exemple), sont négligeables. Les composantes de l’accélération sont alors très simples : \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (nous supposons que le mouvement se produit à des hauteurs suffisamment petites près de la surface de la terre pour que l’accélération due à la gravité soit constante). Puisque l’accélération due à la gravité s’effectue uniquement le long de la direction verticale, \text{a}_\text{x} = 0. Ainsi, les équations cinématiques décrivant le mouvement le long des directions \text{x} et \text{y} respectivement, peuvent être utilisées :
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Nous analysons le mouvement bidimensionnel du projectile en le décomposant en deux mouvements unidimensionnels indépendants selon les axes vertical et horizontal. Le mouvement horizontal est simple, car \text{a}_\text{x} = 0 et \text{v}_\text{x} est donc constant. La vitesse dans la direction verticale commence à diminuer au fur et à mesure qu’un objet s’élève ; à son point le plus haut, la vitesse verticale est nulle. Lorsqu’un objet retombe vers la Terre, la vitesse verticale augmente à nouveau, mais dans la direction opposée à la vitesse verticale initiale. Les mouvements \text{x} et \text{y} peuvent être recombinés pour donner la vitesse totale à tout point donné de la trajectoire.
