- Objectifs d’apprentissage
- Exemple 1. Calcul de l’énergie des photons et de l’effet photoélectrique : Une lumière violette
- Stratégie
- Solution de la partie 1
- Solution de la 2ème partie
- Discussion
- Explorations PhET : Effet photoélectrique
- Résumé de la section
- Questions conceptuelles
- Problèmes &Exercices
- Glossaire
- Solutions choisies aux problèmes &Exercices
Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Décrire une expérience typique d’effet photoélectrique.
- Déterminer l’énergie cinétique maximale des photoélectrons éjectés par des photons d’une énergie ou d’une longueur d’onde, lorsqu’on vous donne l’énergie cinétique maximale des photoélectrons pour une énergie de photon ou une longueur d’onde différente.
Lorsque la lumière frappe des matériaux, elle peut en éjecter des électrons. C’est ce qu’on appelle l’effet photoélectrique, c’est-à-dire que la lumière (photo) produit de l’électricité. Une utilisation courante de l’effet photoélectrique est dans les posemètres, tels que ceux qui ajustent le diaphragme automatique sur divers types d’appareils photo. De la même manière, les cellules solaires, que vous avez probablement dans votre calculatrice ou que vous avez vues sur un toit ou un panneau routier, sont également utilisées. Celles-ci utilisent l’effet photoélectrique pour convertir la lumière en électricité afin de faire fonctionner différents appareils.

Figure 1. L’effet photoélectrique peut être observé en laissant la lumière tomber sur la plaque métallique dans ce tube sous vide. Les électrons éjectés par la lumière sont collectés sur le fil collecteur et mesurés sous forme de courant. Une tension de retardement entre le fil collecteur et la plaque peut alors être ajustée de manière à déterminer l’énergie des électrons éjectés. Par exemple, si elle est suffisamment négative, aucun électron n’atteindra le fil. (crédit : P.P. Urone)
Cet effet est connu depuis plus d’un siècle et peut être étudié à l’aide d’un dispositif tel que celui présenté sur la figure 1. Cette figure montre un tube sous vide avec une plaque métallique et un fil collecteur qui sont reliés par une source de tension variable, le collecteur étant plus négatif que la plaque. Lorsque la lumière (ou un autre rayonnement électromagnétique) frappe la plaque dans le tube sous vide, elle peut éjecter des électrons. Si les électrons ont une énergie en électronvolts (eV) supérieure à la différence de potentiel entre la plaque et le fil en volts, certains électrons seront collectés sur le fil. Puisque l’énergie des électrons en eV est eV, où q est la charge de l’électron et V la différence de potentiel, l’énergie des électrons peut être mesurée en ajustant la tension de retardement entre le fil et la plaque. La tension qui empêche les électrons d’atteindre le fil est égale à l’énergie en eV. Par exemple, si -3,00 V arrête à peine les électrons, leur énergie est de 3,00 eV. Le nombre d’électrons éjectés peut être déterminé en mesurant le courant entre le fil et la plaque. Plus il y a de lumière, plus il y a d’électrons ; un petit circuit permet d’utiliser cet appareil comme un luxmètre.
Ce qui est vraiment important à propos de l’effet photoélectrique, c’est ce qu’Albert Einstein en a déduit. Einstein a réalisé qu’il y avait plusieurs caractéristiques de l’effet photoélectrique qui ne pouvaient être expliquées que si le rayonnement EM est lui-même quantifié : le flux d’énergie apparemment continu d’une onde EM est en fait composé de quanta d’énergie appelés photons. Dans son explication de l’effet photoélectrique, Einstein a défini une unité quantifiée ou quantum d’énergie EM, que nous appelons aujourd’hui photon, avec une énergie proportionnelle à la fréquence du rayonnement EM. Sous forme d’équation, l’énergie du photon est E = hf, où E est l’énergie d’un photon de fréquence f et h est la constante de Planck. Cette idée révolutionnaire ressemble à la quantification de Planck des états d’énergie dans les oscillateurs à corps noir, mais elle est très différente. Il s’agit de la quantification du rayonnement électromagnétique lui-même. Les ondes EM sont composées de photons et ne sont pas des ondes lisses continues comme celles décrites dans les chapitres précédents sur l’optique. Leur énergie est absorbée et émise par paquets, et non de manière continue. Cela correspond exactement à la quantification de Planck des niveaux d’énergie dans les oscillateurs à corps noir, puisque ces oscillateurs augmentent et diminuent leur énergie par paliers de hf en absorbant et en émettant des photons ayant E = hf. Nous ne l’observons pas avec nos yeux, car les sources lumineuses courantes contiennent tellement de photons que les photons individuels passent inaperçus. (Voir figure 2.) La section suivante du texte (Énergies des photons et spectre électromagnétique) est consacrée à une discussion sur les photons et certaines de leurs caractéristiques et implications. Pour l’instant, nous utiliserons le concept de photon pour expliquer l’effet photoélectrique, un peu comme l’a fait Einstein.
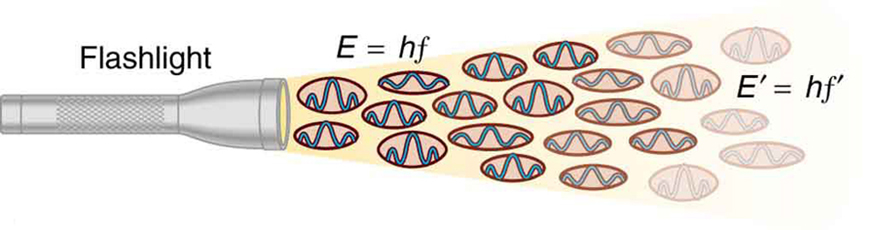
Figure 2. Une onde EM de fréquence f est composée de photons, ou quanta individuels de rayonnement EM. L’énergie de chaque photon est E = hf, où h est la constante de Planck et f est la fréquence du rayonnement EM. Une intensité plus élevée signifie plus de photons par unité de surface. La lampe de poche émet un grand nombre de photons de nombreuses fréquences différentes, donc d’autres ont une énergie E′ = hf′, et ainsi de suite.
L’effet photoélectrique a les propriétés discutées ci-dessous. Toutes ces propriétés sont cohérentes avec l’idée que les photons individuels du rayonnement EM sont absorbés par des électrons individuels dans un matériau, l’électron gagnant l’énergie du photon. Certaines de ces propriétés sont incompatibles avec l’idée que le rayonnement électromagnétique est une simple onde. Pour simplifier, considérons ce qui se passe avec un rayonnement EM monochromatique dans lequel tous les photons ont la même énergie hf.
- Si nous faisons varier la fréquence du rayonnement EM tombant sur un matériau, nous constatons ce qui suit : Pour un matériau donné, il existe une fréquence seuil f0 pour le rayonnement EM en dessous de laquelle aucun électron n’est éjecté, quelle que soit l’intensité. Les photons individuels interagissent avec les électrons individuels. Ainsi, si l’énergie du photon est trop faible pour briser un électron, aucun électron ne sera éjecté. Si le rayonnement EM était une simple onde, on pourrait obtenir une énergie suffisante en augmentant l’intensité.
- Dès que le rayonnement EM tombe sur un matériau, les électrons sont éjectés sans délai. Dès qu’un photon individuel d’une fréquence suffisamment élevée est absorbé par un électron individuel, ce dernier est éjecté. Si le rayonnement EM était une simple onde, plusieurs minutes seraient nécessaires pour qu’une énergie suffisante soit déposée à la surface du métal pour éjecter un électron.
- Le nombre d’électrons éjectés par unité de temps est proportionnel à l’intensité du rayonnement EM et à aucune autre caractéristique. Le rayonnement EM de haute intensité consiste en un grand nombre de photons par unité de surface, tous les photons ayant la même énergie caractéristique hf.
- Si l’on fait varier l’intensité du rayonnement EM et que l’on mesure l’énergie des électrons éjectés, on constate ce qui suit : L’énergie cinétique maximale des électrons éjectés est indépendante de l’intensité du rayonnement EM. Comme il y a tellement d’électrons dans un matériau, il est extrêmement improbable que deux photons interagissent avec le même électron en même temps, augmentant ainsi l’énergie qui lui est donnée. Au lieu de cela (comme indiqué au point 3 ci-dessus), une intensité accrue entraîne l’éjection d’un plus grand nombre d’électrons de même énergie. Si le rayonnement EM était une simple onde, une intensité plus élevée pourrait donner plus d’énergie, et des électrons de plus haute énergie seraient éjectés.
- L’énergie cinétique d’un électron éjecté est égale à l’énergie du photon moins l’énergie de liaison de l’électron dans le matériau spécifique. Un photon individuel peut donner toute son énergie à un électron. L’énergie du photon est en partie utilisée pour détacher l’électron du matériau. Le reste est affecté à l’énergie cinétique de l’électron éjecté. Sous forme d’équation, cette énergie est donnée par KEe = hf – BE, où KEe est l’énergie cinétique maximale de l’électron éjecté, hf est l’énergie du photon et BE est l’énergie de liaison de l’électron au matériau en question. (BE est parfois appelée la fonction de travail du matériau). Cette équation, due à Einstein en 1905, explique quantitativement les propriétés de l’effet photoélectrique. Un photon individuel de rayonnement électromagnétique (il n’y en a pas d’autre) interagit avec un électron individuel, fournissant suffisamment d’énergie, BE, pour le détacher, le reste étant consacré à l’énergie cinétique. L’énergie de liaison est BE = hf0, où f0 est la fréquence seuil pour le matériau particulier. La figure 3 montre un graphique de la KEe maximale en fonction de la fréquence du rayonnement EM incident tombant sur un matériau particulier.
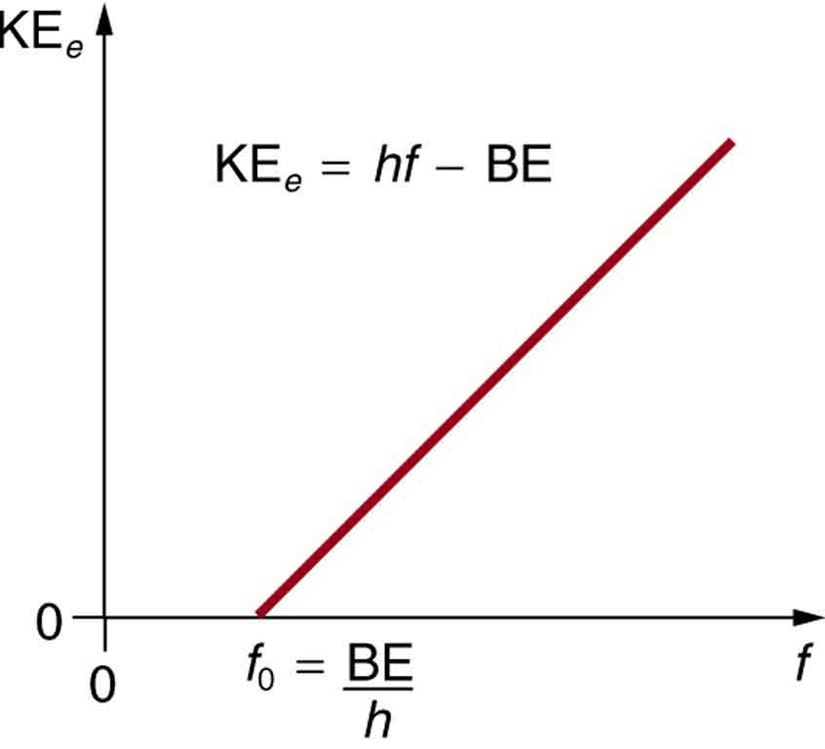
Figure 3. Effet photoélectrique. Un graphique de l’énergie cinétique d’un électron éjecté, KEe, en fonction de la fréquence du rayonnement EM tombant sur un certain matériau. Il existe une fréquence seuil en dessous de laquelle aucun électron n’est éjecté, car le photon individuel qui interagit avec un électron individuel n’a pas assez d’énergie pour le briser. Au-dessus de l’énergie de seuil, KEe augmente linéairement avec f, conformément à KEe = hf – BE. La pente de cette ligne est h – les données peuvent être utilisées pour déterminer expérimentalement la constante de Planck. Einstein a donné la première explication réussie de telles données en proposant l’idée de photons – des quanta de rayonnement EM.
L’idée d’Einstein que le rayonnement EM est quantifié a été cruciale pour les débuts de la mécanique quantique. C’est un concept beaucoup plus général que son explication de l’effet photoélectrique pourrait le laisser entendre. Tout le rayonnement électromagnétique peut également être modélisé sous la forme de photons, et les caractéristiques du rayonnement électromagnétique sont entièrement compatibles avec ce fait. (Comme nous le verrons dans la section suivante, de nombreux aspects du rayonnement EM, tels que les dangers du rayonnement ultraviolet (UV), ne peuvent être expliqués que par les propriétés des photons). Plus célèbre pour la relativité moderne, Einstein a planté une graine importante pour la mécanique quantique en 1905, l’année même où il a publié son premier article sur la relativité restreinte. Son explication de l’effet photoélectrique est à l’origine du prix Nobel qui lui a été décerné en 1921. Bien que ses autres contributions à la physique théorique aient également été soulignées dans ce prix, la relativité restreinte et la relativité générale n’ont pas été pleinement reconnues, bien qu’elles aient été partiellement vérifiées par l’expérience en 1921. Bien qu’adulé comme un héros, ce grand homme n’a jamais reçu de reconnaissance Nobel pour son œuvre la plus célèbre, la relativité.
Exemple 1. Calcul de l’énergie des photons et de l’effet photoélectrique : Une lumière violette
1. Quelle est l’énergie en joules et en électrons-volts d’un photon de lumière violette de 420 nm ?
2. Quelle est l’énergie cinétique maximale des électrons éjectés du calcium par la lumière violette de 420 nm, étant donné que l’énergie de liaison (ou fonction de travail) des électrons pour le calcium métal est de 2,71 eV ?
Stratégie
Pour résoudre la partie 1, notez que l’énergie d’un photon est donnée par E = hf. Pour la partie 2, une fois l’énergie du photon calculée, c’est une application directe de KEe = hf – BE pour trouver l’énergie cinétique maximale de l’électron éjecté, puisque BE est donnée.
Solution de la partie 1
L’énergie du photon est donnée par E = hf.
Puisque l’on nous donne la longueur d’onde plutôt que la fréquence, nous résolvons la relation familière c = fλ pour la fréquence, ce qui donne f=\frac{c}{\lambda}\\\\.
La combinaison de ces deux équations donne la relation utile E=\frac{hc}{\lambda}\.
En substituant maintenant les valeurs connues, on obtient
\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4,74\times10^{-19}\text{ J}\
Converti en eV, l’énergie du photon est
\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}{1.6\times10^{-19}\text{ J}}=2.96\text{ eV}\
Solution de la 2ème partie
La détermination de l’énergie cinétique de l’électron éjecté est maintenant une simple application de l’équation KEe = hf – BE. En substituant l’énergie du photon et l’énergie de liaison, on obtient KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Discussion
L’énergie de ce photon de 420 nm de lumière violette est une minuscule fraction de joule, et il n’est donc pas étonnant qu’un photon unique soit difficile à percevoir directement pour nous – les humains sont plus sensibles aux énergies de l’ordre du joule. Mais si l’on considère l’énergie en électronvolts, on constate que ce photon a suffisamment d’énergie pour affecter les atomes et les molécules. Une molécule d’ADN peut être brisée avec environ 1 eV d’énergie, par exemple, et les énergies atomiques et moléculaires typiques sont de l’ordre de l’eV, de sorte que le photon UV dans cet exemple pourrait avoir des effets biologiques. L’électron éjecté (appelé photoélectron) a une énergie plutôt faible, et il ne se déplacerait pas loin, sauf dans le vide. L’électron serait arrêté par un potentiel retardateur de seulement 0,26 eV. En fait, si la longueur d’onde du photon était plus grande et son énergie inférieure à 2,71 eV, la formule donnerait une énergie cinétique négative, ce qui est impossible. Cela signifie simplement que les photons de 420 nm, avec leur énergie de 2,96 eV, ne dépassent pas de beaucoup le seuil de fréquence. Vous pouvez montrer par vous-même que la longueur d’onde du seuil est de 459 nm (lumière bleue). Cela signifie que si le calcium-métal est utilisé dans un photomètre, celui-ci sera insensible aux longueurs d’onde supérieures à celles de la lumière bleue. Un tel posemètre serait complètement insensible à la lumière rouge, par exemple.
Explorations PhET : Effet photoélectrique
Voyez comment la lumière fait tomber les électrons d’une cible métallique, et recréez l’expérience qui a donné naissance au domaine de la mécanique quantique.

Cliquez pour télécharger la simulation. Exécutez-la en utilisant Java.
Résumé de la section
- L’effet photoélectrique est le processus par lequel le rayonnement EM éjecte des électrons d’un matériau.
- Einstein a proposé que les photons soient des quanta de rayonnement EM ayant une énergie E = hf, où f est la fréquence du rayonnement.
- Tout le rayonnement EM est composé de photons. Comme Einstein l’a expliqué, toutes les caractéristiques de l’effet photoélectrique sont dues à l’interaction de photons individuels avec des électrons individuels.
- L’énergie cinétique maximale KEe des électrons éjectés (photoélectrons) est donnée par KEe = hf – BE, où hf est l’énergie du photon et BE est l’énergie de liaison (ou fonction de travail) de l’électron au matériau particulier.
Questions conceptuelles
- La lumière visible est-elle le seul type de rayonnement EM pouvant provoquer l’effet photoélectrique ?
- Quels aspects de l’effet photoélectrique ne peuvent être expliqués sans photons ? Lesquels peuvent être expliqués sans photons ? Ces derniers sont-ils incompatibles avec l’existence des photons ?
- L’effet photoélectrique est-il une conséquence directe du caractère ondulatoire du rayonnement EM ou du caractère particulaire de ce rayonnement ? Expliquez brièvement.
- Les isolants (non-métaux) ont un BE plus élevé que les métaux, et il est plus difficile pour les photons d’éjecter les électrons des isolants. Discutez du lien entre ce phénomène et les charges libres des métaux qui en font de bons conducteurs.
- Si vous prenez et secouez un morceau de métal qui contient des électrons libres de se déplacer sous forme de courant, aucun électron ne tombe. Pourtant, si vous chauffez le métal, les électrons peuvent être bouillis. Expliquez ces deux faits en relation avec la quantité et la distribution de l’énergie impliquée dans le fait de secouer l’objet par rapport à son chauffage.
Problèmes &Exercices
- Quelle est la plus grande longueur d’onde du rayonnement EM qui peut éjecter un photoélectron de l’argent, étant donné que l’énergie de liaison est de 4,73 eV ? Est-ce dans le domaine visible?
- Trouvez le photon de plus grande longueur d’onde qui peut éjecter un électron du potassium, étant donné que l’énergie de liaison est de 2,24 eV. S’agit-il d’un rayonnement EM visible ?
- Quelle est l’énergie de liaison en eV des électrons du magnésium, si le photon de plus grande longueur d’onde qui peut éjecter des électrons est de 337 nm ?
- Calculez l’énergie de liaison en eV des électrons de l’aluminium, si le photon de plus grande longueur d’onde qui peut les éjecter est de 304 nm.
- Quelle est l’énergie cinétique maximale en eV des électrons éjectés du métal sodium par un rayonnement EM de 450 nm, sachant que l’énergie de liaison est de 2,28 eV?
- Un rayonnement UV ayant une longueur d’onde de 120 nm tombe sur le métal or, auquel les électrons sont liés par 4,82 eV. Quelle est l’énergie cinétique maximale des photoélectrons éjectés?
- La lumière violette de longueur d’onde 400 nm éjecte des électrons d’une énergie cinétique maximale de 0,860 eV du métal sodium. Quelle est l’énergie de liaison des électrons au sodium métal?
- Un rayonnement UV ayant une longueur d’onde de 300 nm tombe sur l’uranium métal, éjectant des électrons de 0,500 eV. Quelle est l’énergie de liaison des électrons à l’uranium métal ?
- (a) Quelle est la longueur d’onde du rayonnement EM qui éjecte des électrons de 2,00 eV du calcium métal, sachant que l’énergie de liaison est de 2,71 eV ? (b) De quel type de rayonnement EM s’agit-il ?
- Trouvez la longueur d’onde des photons qui éjectent des électrons de 0,100 eV du potassium, étant donné que l’énergie de liaison est de 2,24 eV. Ces photons sont-ils visibles ?
- Quelle est la vitesse maximale des électrons éjectés d’un matériau par des photons de 80 nm, s’ils sont liés au matériau par 4,73 eV ?
- Les photoélectrons d’un matériau ayant une énergie de liaison de 2,71 eV sont éjectés par des photons de 420 nm. Une fois éjectés, combien de temps faut-il à ces électrons pour parcourir 2,50 cm jusqu’à un dispositif de détection ?
- Un laser d’une puissance de sortie de 2,00 mW à une longueur d’onde de 400 nm est projeté sur du calcium métal. (a) Combien d’électrons par seconde sont éjectés ? (b) Quelle puissance est emportée par les électrons, sachant que l’énergie de liaison est de 2,71 eV ?
- (a) Calculez le nombre de photoélectrons par seconde éjectés d’une surface de 1,00 mm 2 de sodium métallique par un rayonnement EM de 500 nm ayant une intensité de 1,30 kW/m2 (l’intensité de la lumière solaire au-dessus de l’atmosphère terrestre). (b) Étant donné que l’énergie de liaison est de 2,28 eV, quelle puissance est emportée par les électrons ? (c) Les électrons transportent moins d’énergie que celle apportée par les photons. Où va l’autre puissance ? Comment peut-on la récupérer ?
- Résultats déraisonnables. Une lumière rouge ayant une longueur d’onde de 700 nm est projetée sur du magnésium métallique auquel sont liés des électrons de 3,68 eV. (a) Utilisez KEe = hf – BE pour calculer l’énergie cinétique des électrons éjectés. (b) Qu’est-ce qui n’est pas raisonnable dans ce résultat ? (c) Quelles hypothèses sont déraisonnables ou incohérentes?
- Résultats déraisonnables. (a) Quelle est l’énergie de liaison des électrons à un matériau duquel des électrons de 4.00-eV sont éjectés par un rayonnement EM de 400-nm ? (b) Qu’est-ce qui est déraisonnable dans ce résultat ? (c) Quelles hypothèses sont déraisonnables ou incohérentes ?
Glossaire
effet photoélectrique : le phénomène par lequel certains matériaux éjectent des électrons lorsqu’on les éclaire
photon : un quantum, ou une particule, de rayonnement électromagnétique
énergie du photon : la quantité d’énergie que possède un photon ; E = hf
énergie de liaison : également appelée fonction de travail ; la quantité d’énergie nécessaire pour éjecter un électron d’un matériau
Solutions choisies aux problèmes &Exercices
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm ; (b) Ultraviolet
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s ; (b) 0,256 mW
15. (a) -1,90 eV ; (b) Énergie cinétique négative ; (c) Que les électrons seraient frappés librement.
