Aceleración constante
El análisis del movimiento bidimensional de un proyectil se realiza dividiéndolo en dos movimientos: a lo largo de los ejes horizontal y vertical.
Objetivos de aprendizaje
Analizar el movimiento de un proyectil bidimensional a lo largo de los ejes horizontal y vertical
Puntos clave
Puntos clave
- La aceleración constante en el movimiento en dos dimensiones generalmente sigue un patrón de proyectil.
- El movimiento de proyectil es el movimiento de un objeto lanzado o proyectado al aire, sujeto únicamente a la aceleración (vertical) debida a la gravedad.
- Analizamos el movimiento de proyectil bidimensional dividiéndolo en dos movimientos unidimensionales independientes a lo largo de los ejes vertical y horizontal.
Términos clave
- Cinemático: de o relativo al movimiento o a la cinemática
El movimiento de un proyectil es el movimiento de un objeto lanzado, o proyectado, al aire, sujeto únicamente a la fuerza de la gravedad. El objeto se denomina proyectil, y su trayectoria se denomina trayecto. El movimiento de los objetos que caen es un tipo simple de movimiento de proyectil unidimensional en el que no hay movimiento horizontal. En el movimiento de proyectil bidimensional, como el de un balón de fútbol u otro objeto lanzado, hay un componente vertical y otro horizontal en el movimiento.
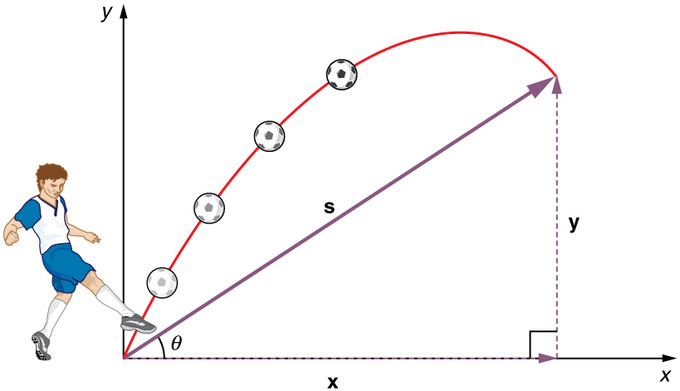
Movimiento de proyectil: Lanzar una piedra o patear una pelota generalmente produce un patrón de movimiento de proyectil que tiene un componente vertical y otro horizontal.
El hecho más importante a recordar es que el movimiento a lo largo de los ejes perpendiculares son independientes y por lo tanto pueden ser analizados por separado. La clave para analizar el movimiento bidimensional del proyectil es dividirlo en dos movimientos, uno a lo largo del eje horizontal y otro a lo largo del vertical. Para describir el movimiento debemos tratar la velocidad y la aceleración, así como el desplazamiento.
Supondremos que todas las fuerzas, excepto la gravedad (como la resistencia del aire y la fricción, por ejemplo) son despreciables. Los componentes de la aceleración son entonces muy simples: \text{a}_\text{y} = -\text{g} = -9,81 \frac{text{m}{\text{s}^2} (suponemos que el movimiento se produce a alturas suficientemente pequeñas cerca de la superficie de la tierra como para que la aceleración debida a la gravedad sea constante). Como la aceleración debida a la gravedad es sólo en la dirección vertical, \text{a}_\text{x} = 0. Por lo tanto, las ecuaciones cinemáticas que describen el movimiento a lo largo de las direcciones \text{x} y \text{y}, respectivamente, se pueden utilizar:
\text{x} = \text{x}_0 + \text{v}_text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
Analizamos el movimiento bidimensional del proyectil dividiéndolo en dos movimientos unidimensionales independientes a lo largo de los ejes vertical y horizontal. El movimiento horizontal es simple, porque \text{a}_\text{x} = 0 y \text{v}_\text{x} es por tanto constante. La velocidad en la dirección vertical comienza a disminuir a medida que un objeto se eleva; en su punto más alto, la velocidad vertical es cero. Cuando un objeto vuelve a caer hacia la Tierra, la velocidad vertical aumenta de nuevo en magnitud, pero apunta en dirección opuesta a la velocidad vertical inicial. Los movimientos \text{x} y \text{y} pueden recombinarse para obtener la velocidad total en cualquier punto de la trayectoria.
