- Objetivos de aprendizaje
- Ejemplo 1. Cálculo de la energía de los fotones y del efecto fotoeléctrico: Una luz violeta
- Estrategia
- Solución para la Parte 1
- Solución de la Parte 2
- Discusión
- PhET Explorations: Efecto fotoeléctrico
- Resumen de la sección
- Preguntas conceptuales
- Problemas & Ejercicios
- Glosario
- Soluciones seleccionadas de problemas &Ejercicios
Objetivos de aprendizaje
Al finalizar esta sección, serás capaz de:
- Describir un experimento típico de efecto fotoeléctrico.
- Determinar la energía cinética máxima de los fotoelectrones expulsados por fotones de una energía o longitud de onda, cuando se da la energía cinética máxima de los fotoelectrones para una energía o longitud de onda de fotones diferente.
Cuando la luz incide en los materiales, puede expulsar electrones de ellos. Esto se llama efecto fotoeléctrico, lo que significa que la luz (foto) produce electricidad. Un uso común del efecto fotoeléctrico es en los medidores de luz, como los que ajustan el iris automático en varios tipos de cámaras. De forma similar, otro uso es en las células solares, como las que probablemente tengas en tu calculadora o hayas visto en un tejado o en una señal de tráfico. Éstas aprovechan el efecto fotoeléctrico para convertir la luz en electricidad para hacer funcionar diferentes dispositivos.

Figura 1. El efecto fotoeléctrico puede observarse dejando caer la luz sobre la placa metálica de este tubo evacuado. Los electrones expulsados por la luz se recogen en el hilo colector y se miden como una corriente. A continuación, se puede ajustar una tensión de retardo entre el hilo colector y la placa para determinar la energía de los electrones expulsados. Por ejemplo, si es lo suficientemente negativa, ningún electrón llegará al cable. (crédito: P.P. Urone)
Este efecto se conoce desde hace más de un siglo y puede estudiarse utilizando un dispositivo como el que se muestra en la figura 1. Esta figura muestra un tubo evacuado con una placa metálica y un hilo colector que están conectados por una fuente de tensión variable, con el colector más negativo que la placa. Cuando la luz (u otra radiación EM) incide en la placa del tubo evacuado, puede expulsar electrones. Si los electrones tienen una energía en electronvoltios (eV) mayor que la diferencia de potencial entre la placa y el cable en voltios, algunos electrones se recogerán en el cable. Como la energía de los electrones en eV es eV, donde q es la carga de los electrones y V es la diferencia de potencial, la energía de los electrones puede medirse ajustando la tensión de retardo entre el hilo y la placa. La tensión que impide que los electrones lleguen al hilo es igual a la energía en eV. Por ejemplo, si -3,00 V apenas detiene los electrones, su energía es de 3,00 eV. El número de electrones expulsados se puede determinar midiendo la corriente entre el cable y la placa. Cuanta más luz, más electrones; un pequeño circuito permite utilizar este dispositivo como medidor de luz.
Lo realmente importante del efecto fotoeléctrico es lo que Albert Einstein dedujo de él. Einstein se dio cuenta de que había varias características del efecto fotoeléctrico que sólo podían explicarse si la radiación EM está cuantificada en sí misma: la corriente aparentemente continua de energía en una onda EM se compone en realidad de cuantos de energía llamados fotones. En su explicación del efecto fotoeléctrico, Einstein definió una unidad cuantificada o quantum de energía EM, que ahora llamamos fotón, con una energía proporcional a la frecuencia de la radiación EM. En forma de ecuación, la energía del fotón es E = hf, donde E es la energía de un fotón de frecuencia f y h es la constante de Planck. Esta idea revolucionaria se parece a la cuantificación de los estados de energía de Planck en los osciladores de cuerpo negro, pero es muy diferente. Es la cuantificación de la propia radiación EM. Las ondas EM están compuestas por fotones y no son ondas continuas y suaves como las descritas en los capítulos anteriores sobre óptica. Su energía se absorbe y se emite en trozos, no de forma continua. Esto es exactamente consistente con la cuantización de Planck de los niveles de energía en los osciladores de cuerpo negro, ya que estos osciladores aumentan y disminuyen su energía en pasos de hf al absorber y emitir fotones que tienen E = hf. No observamos esto con nuestros ojos, porque hay tantos fotones en las fuentes de luz comunes que los fotones individuales pasan desapercibidos. (Véase la figura 2.) La siguiente sección del texto (Energías de los fotones y el espectro electromagnético) está dedicada a la discusión de los fotones y algunas de sus características e implicaciones. Por ahora, utilizaremos el concepto de fotón para explicar el efecto fotoeléctrico, tal y como hizo Einstein.
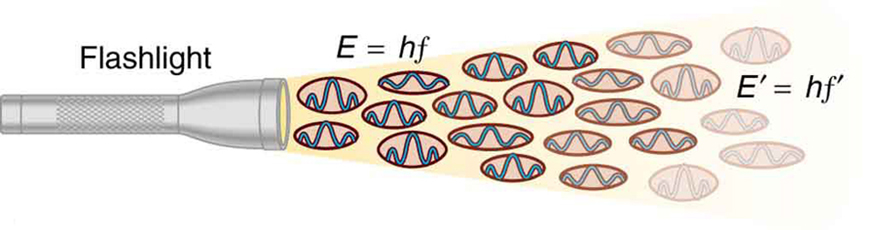
Figura 2. Una onda EM de frecuencia f está compuesta por fotones, o cuantos individuales de radiación EM. La energía de cada fotón es E = hf, donde h es la constante de Planck y f es la frecuencia de la radiación EM. Una mayor intensidad significa más fotones por unidad de superficie. La linterna emite un gran número de fotones de muchas frecuencias diferentes, de ahí que otros tengan energía E′ = hf′, y así sucesivamente.
El efecto fotoeléctrico tiene las propiedades que se comentan a continuación. Todas estas propiedades son consistentes con la idea de que los fotones individuales de la radiación EM son absorbidos por electrones individuales en un material, ganando el electrón la energía del fotón. Algunas de estas propiedades son inconsistentes con la idea de que la radiación EM es una simple onda. Para simplificar, consideremos lo que ocurre con la radiación EM monocromática en la que todos los fotones tienen la misma energía hf.
- Si variamos la frecuencia de la radiación EM que incide sobre un material, encontramos lo siguiente: Para un material dado, existe una frecuencia umbral f0 para la radiación EM por debajo de la cual no se expulsan electrones, independientemente de la intensidad. Los fotones individuales interactúan con electrones individuales. Por tanto, si la energía del fotón es demasiado pequeña para romper un electrón, no se expulsarán electrones. Si la radiación EM fuera una simple onda, se podría obtener suficiente energía aumentando la intensidad.
- Una vez que la radiación EM cae sobre un material, los electrones son expulsados sin demora. Tan pronto como un fotón individual de una frecuencia suficientemente alta es absorbido por un electrón individual, el electrón es expulsado. Si la radiación EM fuera una simple onda, se necesitarían varios minutos para que se depositara suficiente energía en la superficie del metal para expulsar un electrón.
- El número de electrones expulsados por unidad de tiempo es proporcional a la intensidad de la radiación EM y a ninguna otra característica. La radiación EM de alta intensidad consiste en un gran número de fotones por unidad de superficie, teniendo todos los fotones la misma energía característica hf.
- Si variamos la intensidad de la radiación EM y medimos la energía de los electrones expulsados, encontramos lo siguiente: La energía cinética máxima de los electrones expulsados es independiente de la intensidad de la radiación EM. Como hay tantos electrones en un material, es extremadamente improbable que dos fotones interactúen con el mismo electrón al mismo tiempo, aumentando así la energía que se le da. En su lugar (como se indica en el punto 3), el aumento de la intensidad hace que se expulsen más electrones de la misma energía. Si la radiación EM fuera una simple onda, una mayor intensidad podría dar más energía, y se expulsarían electrones de mayor energía.
- La energía cinética de un electrón expulsado es igual a la energía del fotón menos la energía de enlace del electrón en el material específico. Un fotón individual puede dar toda su energía a un electrón. La energía del fotón se utiliza en parte para separar el electrón del material. El resto se destina a la energía cinética del electrón expulsado. En forma de ecuación, esto viene dado por KEe = hf – BE, donde KEe es la energía cinética máxima del electrón expulsado, hf es la energía del fotón y BE es la energía de enlace del electrón con el material concreto. (Esta ecuación, debida a Einstein en 1905, explica cuantitativamente las propiedades del efecto fotoeléctrico. Un fotón individual de radiación EM (no viene de otra manera) interactúa con un electrón individual, suministrando suficiente energía, BE, para romperlo, y el resto va a la energía cinética. La energía de enlace es BE = hf0, donde f0 es la frecuencia umbral para el material concreto. La figura 3 muestra un gráfico de la KEe máxima frente a la frecuencia de la radiación EM incidente que incide sobre un material concreto.
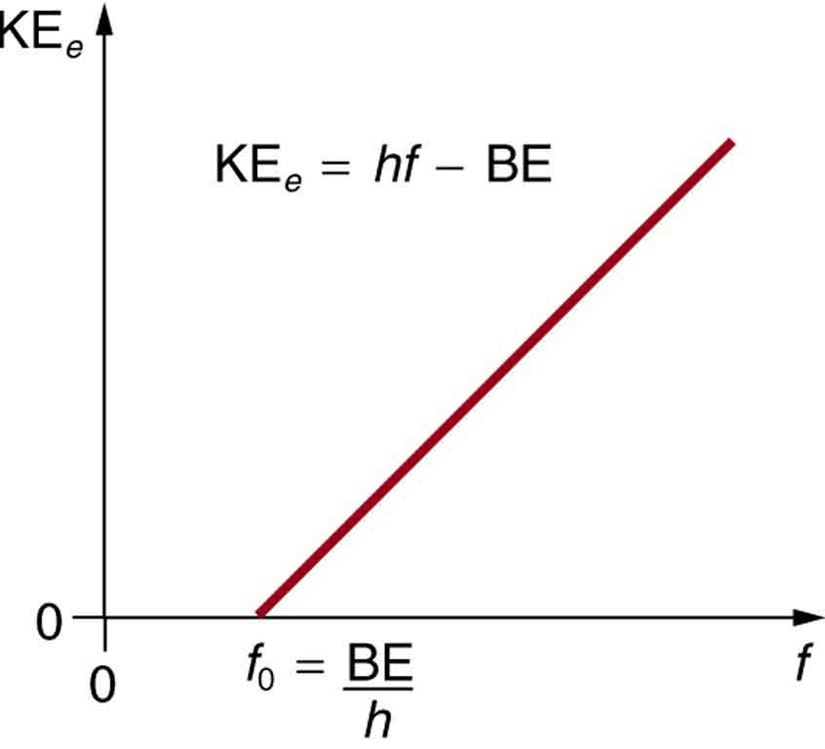
Figura 3. Efecto fotoeléctrico. Gráfico de la energía cinética de un electrón expulsado, KEe, frente a la frecuencia de la radiación EM que incide sobre un determinado material. Existe una frecuencia umbral por debajo de la cual no se expulsan electrones, porque el fotón individual que interactúa con un electrón individual no tiene energía suficiente para romperlo. Por encima del umbral de energía, el KEe aumenta linealmente con f, de acuerdo con KEe = hf – BE. La pendiente de esta línea es h-los datos pueden utilizarse para determinar la constante de Planck experimentalmente. Einstein dio la primera explicación exitosa de tales datos proponiendo la idea de los fotones-cuantos de radiación EM.
La idea de Einstein de que la radiación EM está cuantizada fue crucial para los inicios de la mecánica cuántica. Es un concepto mucho más general de lo que su explicación del efecto fotoeléctrico podría implicar. Toda la radiación EM puede modelarse también en forma de fotones, y las características de la radiación EM son totalmente coherentes con este hecho. (Como veremos en la siguiente sección, muchos aspectos de la radiación EM, como los peligros de la radiación ultravioleta (UV), sólo pueden explicarse por las propiedades de los fotones). Más famoso por la relatividad moderna, Einstein plantó una importante semilla para la mecánica cuántica en 1905, el mismo año en que publicó su primer artículo sobre la relatividad especial. Su explicación del efecto fotoeléctrico fue la base del Premio Nobel que se le concedió en 1921. Aunque sus otras contribuciones a la física teórica también fueron señaladas en ese premio, la relatividad especial y general no fueron plenamente reconocidas a pesar de haber sido parcialmente verificadas por el experimento en 1921. Aunque fue adorado como un héroe, este gran hombre nunca recibió el reconocimiento del Nobel por su obra más famosa: la relatividad.
Ejemplo 1. Cálculo de la energía de los fotones y del efecto fotoeléctrico: Una luz violeta
1. ¿Cuál es la energía en julios y electronvoltios de un fotón de luz violeta de 420 nm?
2. ¿Cuál es la energía cinética máxima de los electrones expulsados del calcio por la luz violeta de 420 nm, dado que la energía de enlace (o función de trabajo) de los electrones para el calcio metal es de 2,71 eV?
Estrategia
Para resolver la Parte 1, observe que la energía de un fotón viene dada por E = hf. Para la Parte 2, una vez calculada la energía del fotón, es una aplicación directa de KEe = hf – BE para encontrar la energía cinética máxima del electrón expulsado, ya que BE está dada.
Solución para la Parte 1
La energía del fotón viene dada por E = hf.
Como se nos da la longitud de onda en lugar de la frecuencia, resolvemos la conocida relación c = fλ para la frecuencia, lo que da como resultado f=\frac{c}{lambda}\\f.
Combinando estas dos ecuaciones se obtiene la útil relación E=\frac{hc}{lambda}\f.
Ahora, sustituyendo los valores conocidos, se obtiene
displaystyle{E}=frac{{i}(6,63 veces10^{-34}{texto{ J}{cdot{texto}{derecho})}(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4,74\times10^{-19}\text{ J}\
Convirtiendo a eV, la energía del fotón es
displaystyle{E}=\left(4.47 veces10^19}\\️ derecha)\️{1\️{ eV}}{1,6 veces10^19}\️{ J}}=2,96\️{ eV}{4478>
Solución de la Parte 2
Hallar la energía cinética del electrón expulsado es ahora una simple aplicación de la ecuación KEe = hf – BE. Sustituyendo la energía del fotón y la energía de enlace se obtiene KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Discusión
La energía de este fotón de 420 nm de luz violeta es una pequeña fracción de un julio, por lo que no es de extrañar que un solo fotón nos resulte difícil de percibir directamente; los humanos estamos más acostumbrados a energías del orden de los julios. Pero si observamos la energía en electronvoltios, podemos ver que este fotón tiene suficiente energía para afectar a átomos y moléculas. Una molécula de ADN puede romperse con aproximadamente 1 eV de energía, por ejemplo, y las energías atómicas y moleculares típicas son del orden de los eV, por lo que el fotón UV de este ejemplo podría tener efectos biológicos. El electrón expulsado (llamado fotoelectrón) tiene una energía bastante baja, y no viajaría lejos, excepto en el vacío. El electrón sería detenido por un potencial de retardo de sólo 0,26 eV. De hecho, si la longitud de onda del fotón fuera mayor y su energía inferior a 2,71 eV, la fórmula daría una energía cinética negativa, algo imposible. Esto significa simplemente que los fotones de 420 nm con su energía de 2,96 eV no están muy por encima del umbral de frecuencia. Puedes demostrar por ti mismo que la longitud de onda umbral es de 459 nm (luz azul). Esto significa que si se utiliza calcio metal en un medidor de luz, éste será insensible a las longitudes de onda más largas que las de la luz azul. Un medidor de luz de este tipo sería completamente insensible a la luz roja, por ejemplo.
PhET Explorations: Efecto fotoeléctrico
Vea cómo la luz desprende electrones de un objetivo metálico y recree el experimento que dio origen al campo de la mecánica cuántica.

Haga clic para descargar la simulación. Ejecutar usando Java.
Resumen de la sección
- El efecto fotoeléctrico es el proceso en el que la radiación EM expulsa electrones de un material.
- Einstein propuso que los fotones son cuantos de radiación EM que tienen energía E = hf, donde f es la frecuencia de la radiación.
- Toda la radiación EM está compuesta por fotones. Como explicó Einstein, todas las características del efecto fotoeléctrico se deben a la interacción de fotones individuales con electrones individuales.
- La energía cinética máxima KEe de los electrones expulsados (fotoelectrones) viene dada por KEe = hf – BE, donde hf es la energía del fotón y BE es la energía de enlace (o función de trabajo) del electrón con el material concreto.
Preguntas conceptuales
- ¿Es la luz visible el único tipo de radiación EM que puede causar el efecto fotoeléctrico?
- ¿Qué aspectos del efecto fotoeléctrico no se pueden explicar sin fotones? Cuáles pueden explicarse sin fotones? Son estos últimos inconsistentes con la existencia de fotones?
- ¿Es el efecto fotoeléctrico una consecuencia directa del carácter ondulatorio de la radiación EM o del carácter de partícula de la radiación EM? Explique brevemente.
- Los aislantes (no metales) tienen un BE mayor que los metales, y es más difícil que los fotones expulsen electrones de los aislantes. Discuta cómo esto se relaciona con las cargas libres en los metales que los hacen buenos conductores.
- Si usted toma y agita un pedazo de metal que tiene electrones libres para moverse como una corriente, no caen electrones. Sin embargo, si calientas el metal, los electrones pueden desprenderse. Explique ambos hechos en relación con la cantidad y la distribución de la energía involucrada con la agitación del objeto en comparación con el calentamiento.
Problemas & Ejercicios
- ¿Cuál es la radiación EM de mayor longitud de onda que puede expulsar un fotoelectrón de la plata, dado que la energía de enlace es de 4,73 eV? ¿Está esto en el rango visible?
- Encuentre el fotón de mayor longitud de onda que puede expulsar un electrón del potasio, dado que la energía de enlace es de 2,24 eV. ¿Es ésta una radiación EM visible?
- ¿Cuál es la energía de enlace en eV de los electrones del magnesio, si el fotón de mayor longitud de onda que puede expulsar electrones es de 337 nm?
- Calcule la energía de enlace en eV de los electrones del aluminio, si el fotón de mayor longitud de onda que puede expulsarlos es de 304 nm.
- ¿Cuál es la máxima energía cinética en eV de los electrones expulsados del metal sodio por una radiación EM de 450 nm, dado que la energía de enlace es de 2,28 eV?
- La radiación UV que tiene una longitud de onda de 120 nm incide sobre el metal oro, al que los electrones están ligados 4,82 eV. ¿Cuál es la energía cinética máxima de los fotoelectrones expulsados?
- La luz violeta de longitud de onda 400 nm expulsa electrones con una energía cinética máxima de 0,860 eV del metal sodio. ¿Cuál es la energía de enlace de los electrones con el sodio metálico?
- Una radiación UV de 300 nm de longitud de onda incide sobre el uranio metálico, expulsando electrones de 0,500 eV. ¿Cuál es la energía de enlace de los electrones con el uranio metálico?
- (a) ¿Cuál es la longitud de onda de la radiación EM que expulsa electrones de 2,00 eV del calcio metálico, dado que la energía de enlace es de 2,71 eV? (b) ¿De qué tipo de radiación EM se trata?
- Encuentra la longitud de onda de los fotones que expulsan electrones de 0,100 eV del potasio, dado que la energía de enlace es de 2,24 eV. ¿Son visibles estos fotones?
- ¿Cuál es la velocidad máxima de los electrones expulsados de un material por fotones de 80-nm, si están ligados al material por 4,73 eV?
- Los fotoelectrones de un material con una energía de enlace de 2,71 eV son expulsados por fotones de 420-nm. Una vez expulsados, ¿cuánto tiempo tardan estos electrones en viajar 2,50 cm hasta un dispositivo de detección?
- Un láser con una potencia de salida de 2,00 mW a una longitud de onda de 400 nm se proyecta sobre calcio metálico. (a) ¿Cuántos electrones por segundo son expulsados? (b) ¿Qué potencia se llevan los electrones, dado que la energía de enlace es de 2,71 eV?
- (a) Calcule el número de fotoelectrones por segundo expulsados de un área de 1,00 mm 2 de metal de sodio por una radiación EM de 500 nm que tiene una intensidad de 1,30 kW/m2 (la intensidad de la luz solar por encima de la atmósfera terrestre). (b) Dado que la energía de enlace es de 2,28 eV, ¿qué potencia se llevan los electrones? (c) Los electrones se llevan menos energía que la aportada por los fotones. ¿A dónde va la otra energía? ¿Cómo se puede recuperar?
- Resultados no razonables. Una luz roja con una longitud de onda de 700 nm se proyecta sobre un metal de magnesio al que los electrones están unidos por 3,68 eV. (a) Utilice KEe = hf – BE para calcular la energía cinética de los electrones expulsados. (b) ¿Qué no es razonable en este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
- Resultados irrazonables. (a) ¿Cuál es la energía de unión de los electrones a un material del que se expulsan electrones de 4,00 eV por radiación EM de 400 nm? (b) ¿Qué es lo irrazonable de este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
Glosario
efecto fotoeléctrico: fenómeno por el que algunos materiales expulsan electrones cuando se les ilumina con luz
fotón: un quantum, o partícula, de radiación electromagnética
energía del fotón: la cantidad de energía que tiene un fotón; E = hf
energía de enlace: también llamada función de trabajo; la cantidad de energía necesaria para expulsar un electrón de un material
Soluciones seleccionadas de problemas &Ejercicios
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm; (b) Ultravioleta
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) Energía cinética negativa; (c) Que los electrones queden libres.
