Konstante Beschleunigung
Die Analyse einer zweidimensionalen Projektilbewegung erfolgt durch Zerlegung in zwei Bewegungen: entlang der horizontalen und vertikalen Achse.
Lernziele
Analysieren Sie eine zweidimensionale Projektilbewegung entlang horizontaler und vertikaler Achsen
Key Takeaways
Key Points
- Konstante Beschleunigung in der Bewegung in zwei Dimensionen folgt im Allgemeinen einem Projektilmuster.
- Projektilbewegung ist die Bewegung eines in die Luft geworfenen oder geschleuderten Objekts, das nur der (vertikalen) Erdbeschleunigung unterliegt.
- Wir analysieren die zweidimensionale Projektilbewegung, indem wir sie in zwei unabhängige eindimensionale Bewegungen entlang der vertikalen und horizontalen Achse zerlegen.
Schlüsselbegriffe
- kinematisch: von oder in Bezug auf Bewegung oder Kinematik
Projektilbewegung ist die Bewegung eines in die Luft geworfenen oder geschleuderten Objekts, das nur der Schwerkraft unterliegt. Das Objekt wird als Projektil bezeichnet, und sein Weg wird als Flugbahn bezeichnet. Die Bewegung fallender Objekte ist eine einfache eindimensionale Form der Projektilbewegung, bei der es keine horizontale Bewegung gibt. Bei zweidimensionalen Projektilbewegungen, wie z. B. bei einem Fußball oder einem anderen geworfenen Gegenstand, gibt es sowohl eine vertikale als auch eine horizontale Komponente der Bewegung.
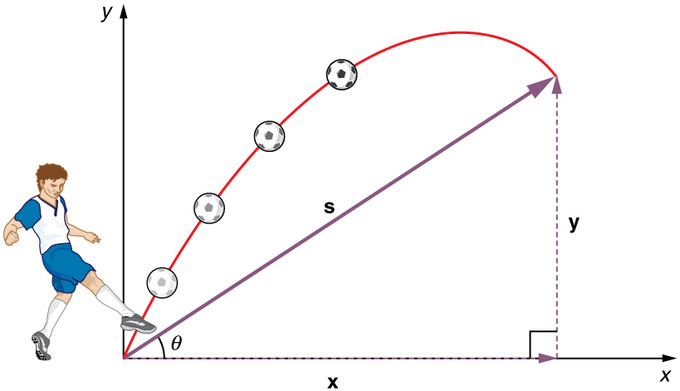
Projektilbewegung: Das Werfen eines Steins oder das Treten eines Balls erzeugt im Allgemeinen ein Projektilbewegungsmuster, das sowohl eine vertikale als auch eine horizontale Komponente hat.
Die wichtigste Tatsache, die man sich merken muss, ist, dass Bewegungen entlang senkrechter Achsen unabhängig sind und daher getrennt analysiert werden können. Der Schlüssel zur Analyse der zweidimensionalen Projektilbewegung besteht darin, sie in zwei Bewegungen aufzuteilen, eine entlang der horizontalen Achse und eine entlang der vertikalen. Um die Bewegung zu beschreiben, müssen wir uns mit der Geschwindigkeit und der Beschleunigung sowie mit der Verschiebung befassen.
Wir nehmen an, dass alle Kräfte außer der Schwerkraft (wie z.B. Luftwiderstand und Reibung) vernachlässigbar sind. Die Komponenten der Beschleunigung sind dann sehr einfach: \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (wir nehmen an, dass die Bewegung in ausreichend kleinen Höhen nahe der Erdoberfläche stattfindet, so dass die Erdbeschleunigung konstant ist). Da die Erdbeschleunigung nur in vertikaler Richtung wirkt, ist \text{a}_\text{x} = 0. Somit können die kinematischen Gleichungen, die die Bewegung entlang der \text{x}- bzw. \text{y}-Richtung beschreiben, verwendet werden:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Wir analysieren die zweidimensionale Projektilbewegung, indem wir sie in zwei unabhängige eindimensionale Bewegungen entlang der vertikalen und horizontalen Achsen zerlegen. Die horizontale Bewegung ist einfach, weil \text{a}_\text{x} = 0 und \text{v}_\text{x} somit konstant ist. Die Geschwindigkeit in vertikaler Richtung nimmt ab, wenn ein Objekt aufsteigt; an seinem höchsten Punkt ist die vertikale Geschwindigkeit gleich Null. Wenn ein Objekt wieder in Richtung Erde fällt, nimmt die Vertikalgeschwindigkeit wieder zu, weist aber in die entgegengesetzte Richtung zur anfänglichen Vertikalgeschwindigkeit. Die Bewegungen \text{x} und \text{y} können rekombiniert werden, um die Gesamtgeschwindigkeit an jedem beliebigen Punkt der Flugbahn zu erhalten.
