Konstant acceleration
Analyse af to-dimensionel projektilbevægelse sker ved at opdele den i to bevægelser: langs den horisontale og den vertikale akse.
Læringsmål
Analyse af en todimensionel projektilbevægelse langs vandrette og lodrette akser
Nøgleudbytte
Nøglepunkter
- Konstant acceleration i bevægelse i to dimensioner følger generelt et projektilmønster.
- Projektilbevægelse er bevægelsen af en genstand, der kastes eller projiceres i luften, og som kun er underlagt den (vertikale) acceleration, der skyldes tyngdekraften.
- Vi analyserer to-dimensionel projektilbevægelse ved at opdele den i to uafhængige endimensionelle bevægelser langs den vertikale og den horisontale akse.
Nøglebegreber
- kinematisk: af eller vedrørende bevægelse eller kinematik
Projektilbevægelse er bevægelsen af et objekt, der kastes, eller projiceres, i luften, kun underlagt tyngdekraften. Genstanden kaldes et projektil, og dens vej kaldes dens bane. Bevægelsen af faldende genstande er en simpel endimensional type projektilbevægelse, hvor der ikke er nogen horisontal bevægelse. I todimensionelle projektilbevægelser, som f.eks. en fodbold eller en anden kastet genstand, er der både en vertikal og en horisontal komponent i bevægelsen.
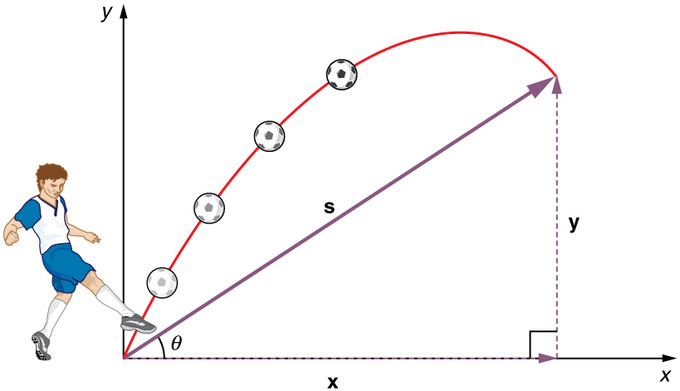
Projektilbevægelse: Når man kaster en sten eller sparker til en bold, opstår der generelt et projektilbevægelsesmønster, som har både en lodret og en vandret komponent.
Det vigtigste faktum at huske er, at bevægelser langs vinkelrette akser er uafhængige og derfor kan analyseres separat. Nøglen til at analysere todimensionel projektilbevægelse er at opdele den i to bevægelser, en langs den vandrette akse og en langs den lodrette. For at beskrive bevægelsen må vi beskæftige os med hastighed og acceleration samt med forskydning.
Vi vil antage, at alle kræfter bortset fra tyngdekraften (som f.eks. luftmodstand og friktion) er ubetydelige. Accelerationens komponenter er så meget enkle: \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (vi antager, at bevægelsen sker i tilstrækkelig lille højde nær jordens overflade, så tyngdeaccelerationen er konstant). Da tyngdeaccelerationen kun er langs den lodrette retning, er \text{a}_\text{x} = 0. Dermed kan de kinematiske ligninger, der beskriver bevægelsen langs henholdsvis \text{x} og \text{y}-retningen, anvendes:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Vi analyserer todimensionel projektilbevægelse ved at opdele den i to uafhængige endimensionelle bevægelser langs den lodrette og den vandrette akse. Den horisontale bevægelse er enkel, fordi \text{a}_\text{x} = 0 og \text{v}_\text{x} er således konstant. Hastigheden i lodret retning begynder at falde, når et objekt stiger; på det højeste punkt er den lodrette hastighed nul. Når et objekt falder mod jorden igen, stiger den lodrette hastighed igen i størrelse, men peger i den modsatte retning af den oprindelige lodrette hastighed. Bevægelserne \text{x} og \text{y} kan kombineres for at give den samlede hastighed i et givet punkt på banen.
