Datové struktury 101: Pole – názorný úvod pro začátečníky

Poznejte datové struktury, které používáte každý den.

👋 Vítejte! Začněme s některými životně důležitými souvislostmi. Dovolte mi, abych se vás na něco zeptal:
✅ Posloucháte hudbu na svém chytrém telefonu?
✅ Vedete si v telefonu seznam kontaktů?
✅ Viděli jste někdy při soutěži žebříček?

Pokud je vaše odpověď na některou z těchto otázek „ano“, pak je téměř jisté, že jste používali pole a ani jste o tom nevěděli! 😃 Pole jsou velmi výkonné datové struktury, které uchovávají seznamy prvků. Mají nekonečně mnoho aplikací. Ve světě informatiky jsou velmi důležité.

V tomto článku se dozvíte výhody a nevýhody polí, jejich strukturu, operace a případy použití.

Začněme! 👍

🔎 Hluboký ponor do základní struktury polí

Abyste pochopili, jak fungují, je velmi užitečné představit si paměť počítače jako mřížku, stejně jako na obrázku níže. Každá informace je uložena v jednom z těchto malých prvků (čtverců), které tvoří mřížku.

Mřížky využívají této „mřížkové“ struktury k ukládání seznamů souvisejících informací na sousedních místech paměti, což zaručuje mimořádnou efektivitu při vyhledávání těchto hodnot. 🔳🔳🔳🔳 🔳

Můžete si pole představit takto:

Jejich prvky jsou v paměti vedle sebe. Pokud potřebujete přistupovat k více než jednomu z nich, je tento proces mimořádně optimalizovaný, protože počítač již ví, kde se daná hodnota nachází.

Úžasné, že? Pojďme se dozvědět, jak to funguje v zákulisí! 😃

📚 Klasifikace

Mřížky se řadí mezi homogenní datové struktury, protože uchovávají prvky stejného typu.

Mohou uchovávat čísla, řetězce, logické hodnoty (true a false), znaky, objekty atd. Jakmile však definujete typ hodnot, které bude pole uchovávat, musí být všechny jeho prvky stejného typu. Nemůžete „míchat“ různé typy dat.

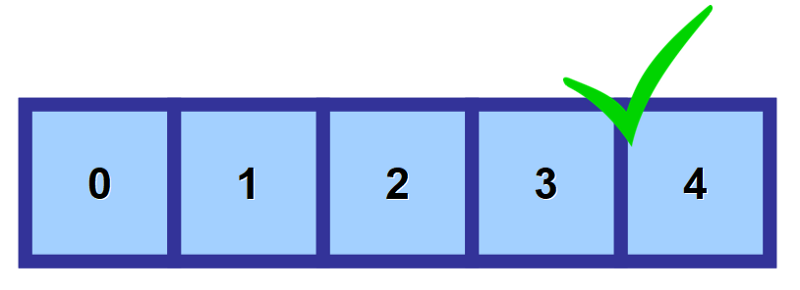
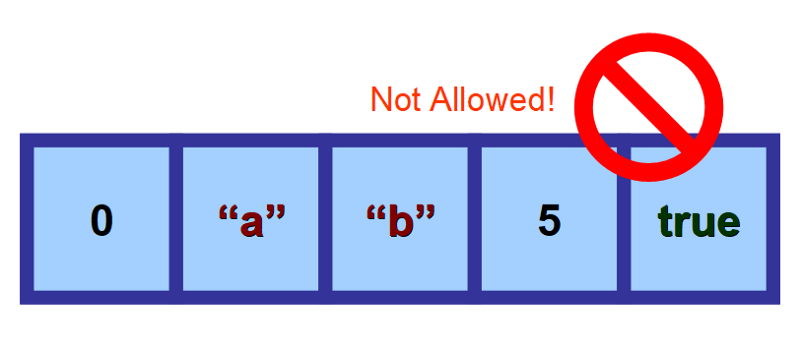
👀 Čtení hodnot – kouzlo začíná!“

Úžasná síla polí vychází z jejich efektivity při přístupu k hodnotám. Toho je dosaženo díky jejich mřížkové struktuře. Pojďme se na ni podívat podrobněji 🔍

Při vytváření pole:
– Přiřadíte jej proměnné. 👈
– Definujete typ prvků, které bude uchovávat. 🎈
– Definujete jeho velikost (maximální počet prvků). 📚

💡 Poznámka: Jméno, které této proměnné přiřadíte, je velmi důležité, protože ho budete později v kódu používat k přístupu k hodnotám a k úpravám pole.

Ale jak počítači řeknete, ke které konkrétní hodnotě chcete přistupovat? Zde hrají důležitou roli indexy!

1️⃣ Indexy

Pro přístup k hodnotě v poli používáte takzvaný „index“ (v množném čísle „indexy“). Jedná se o číslo, které odkazuje na místo, kde je hodnota uložena.

Jak vidíte na obrázku níže, na první prvek v poli se odkazuje pomocí indexu 0. Jak postupujete dále doprava, index se zvyšuje o jedničku pro každé místo v paměti.

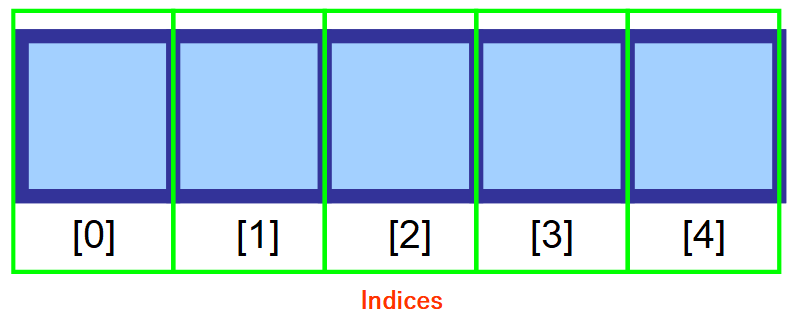
💡 Poznámka: Vím, že se na první pohled zdá divné začínat počítat od 0 místo od 1, ale tomu se říká číslování založené na nule. V informatice je velmi rozšířené.

Obecná syntaxe pro přístup k prvku je následující: <ArrayVariable>

Příklad:
Pokud je vaše pole uloženo v proměnné myArray a vy chcete přistoupit k prvnímu prvku (na indexu 0), použijete myArray

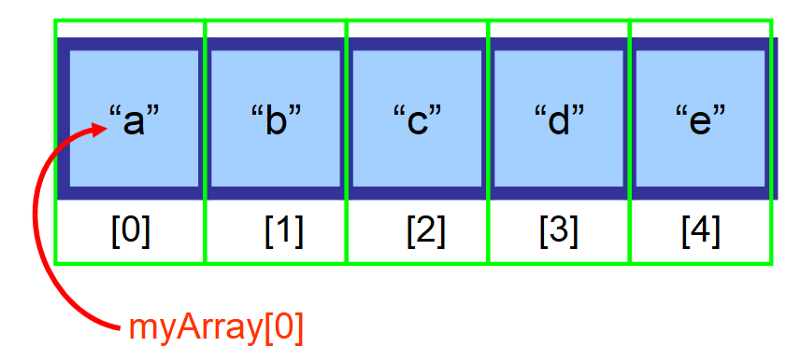
2️⃣ Paměť

Teď, když víte, jak přistupovat k hodnotám, podívejme se, jak jsou pole uložena v paměti počítače. Když definujete velikost pole, celý tento prostor v paměti je od tohoto okamžiku „rezervován“ pro budoucí hodnoty, které budete chtít vložit.

💡 Poznámka: Pokud pole nenaplníte hodnotami, bude tento prostor udržován rezervovaný a prázdný, dokud tak neučiníte.

Pro příklad:
Řekněme, že definujete pole o velikosti 5, ale vložíte pouze jednu hodnotu. Celý tento zbývající prostor bude v paměti prázdný a „rezervovaný“ a bude čekat na budoucí přiřazení.

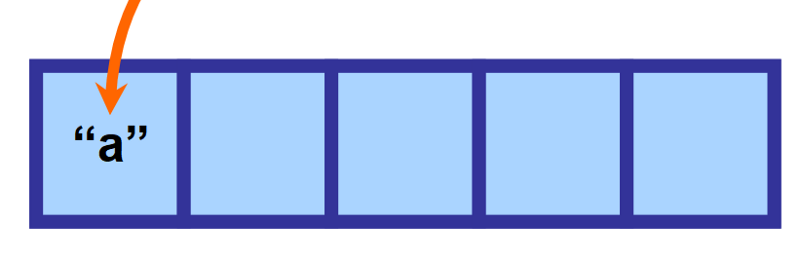
Toto je klíčové, protože pole jsou mimořádně efektivní v přístupu k hodnotám, protože všechny prvky jsou uloženy v souvislých prostorech v paměti. Počítač tak přesně ví, kde má hledat požadované informace.

Ale… má to i svou nevýhodu 😞, protože to není paměťově efektivní. Rezervujete si paměť pro budoucí operace, které nemusí nastat. Proto se pole doporučují v situacích, kdy předem víte, kolik prvků budete ukládat.

🔧 Operace – v zákulisí!

Když už víte, co jsou to pole, když se používají, a jak se v nich ukládají prvky, ponoříme se do jejich operací, jako je vkládání a odstraňování.

1️⃣ Vkládání – vítejte!

Řekněme, že máme pole o velikosti 6 a je v něm ještě prázdné místo. Chceme vložit prvek „e“ na začátek pole (index 0), ale toto místo je již obsazeno prvkem „a“. Co máme dělat?“

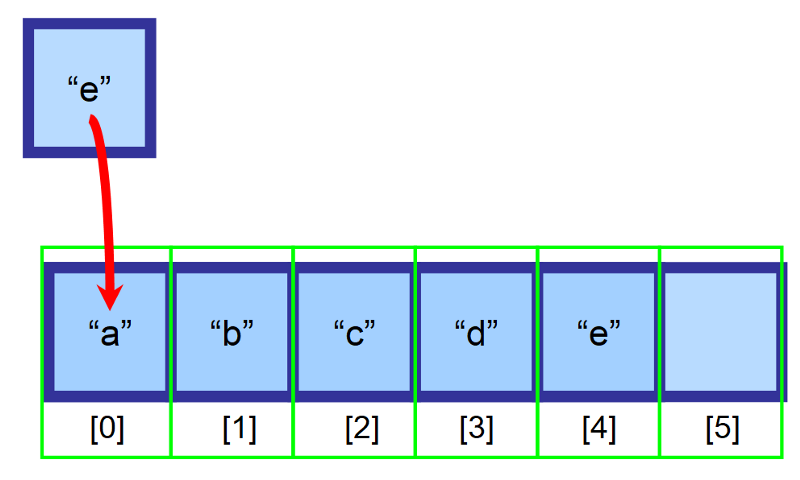
Při vkládání do polí přesuneme všechny prvky, které se nacházejí napravo od místa vložení, o jeden index doprava. Prvek „a“ bude nyní na indexu 1, prvek „b“ bude na indexu 2 a tak dále…

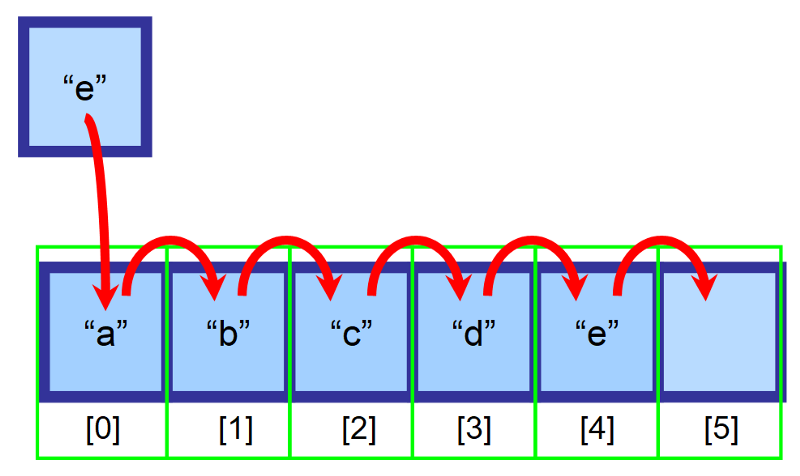
💡 Poznámka: Budete muset vytvořit proměnnou, která bude sledovat poslední index obsahující prvky. Ve výše uvedeném schématu je pole před vložením naplněno až po index 4. Tímto způsobem můžete zjistit, zda je pole plné a jaký index máte použít pro vložení prvku na konec.

Po provedení tohoto úkonu je náš prvek úspěšně vložen. 👏

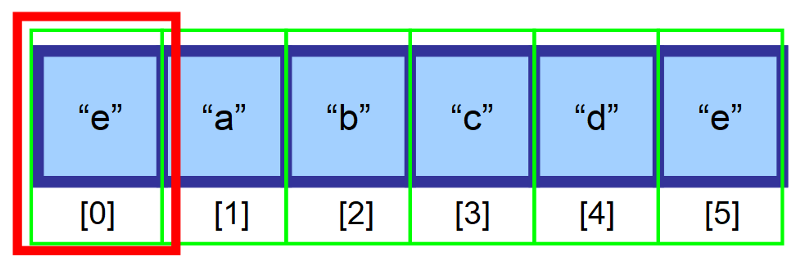
⚠️ Počkat! Co se stane, když je pole plné?“

Co myslíte, že se stane, když je pole plné a vy se pokusíte vložit prvek? 😱

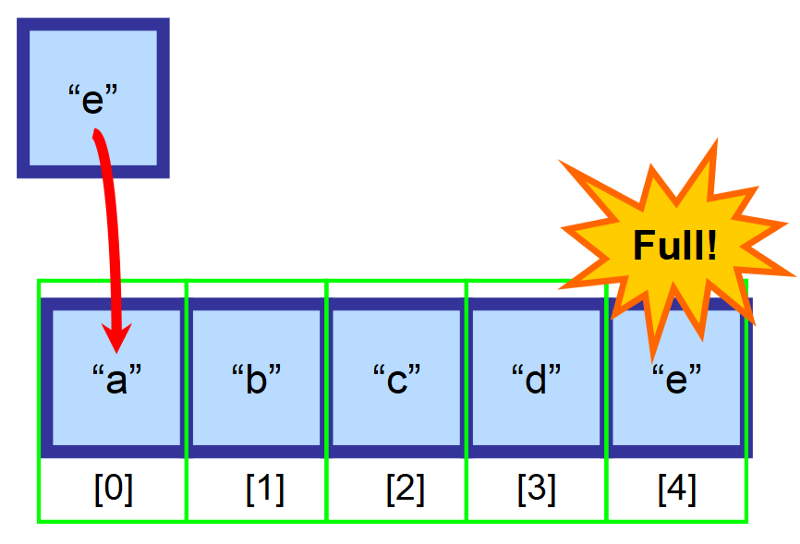
V takovém případě musíte vytvořit nové, větší pole a všechny prvky do něj ručně zkopírovat. Tato operace je časově velmi náročná. Představte si, co by se stalo, kdybyste měli pole s miliony prvků! To by mohlo trvat velmi dlouho. ⏳

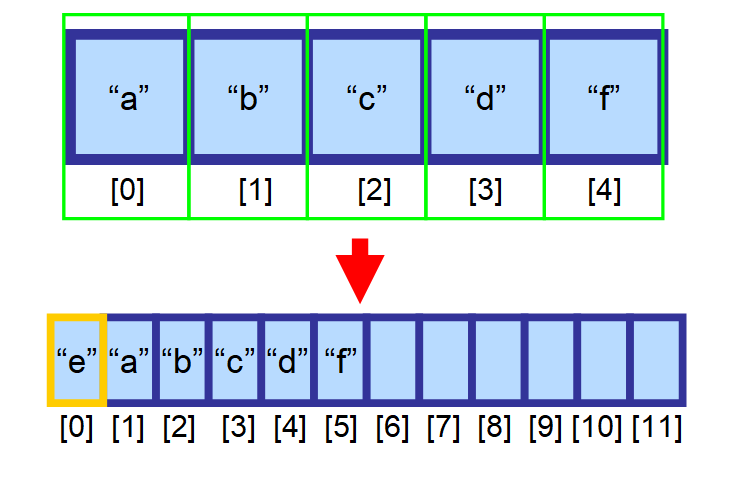
💡 Poznámka: Jedinou výjimkou z tohoto pravidla, kdy je vkládání velmi rychlé, je situace, kdy vložíte prvek na konec pole (na index umístěný vpravo od posledního prvku) a je ještě volné místo. To se provádí v konstantním čase O(1).

2️⃣ Vymazání – sbohem, sbohem!“

Teď řekněme, že chcete vymazat prvek z pole.

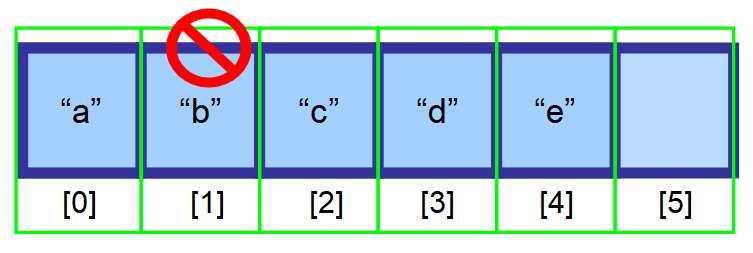
Pro zachování efektivity náhodného přístupu (možnost přistupovat k poli přes index extrémně rychle) musí být prvky uloženy v sousedních prostorech paměti. Nemůžete prostě vymazat prvek a nechat tento prostor prázdný.

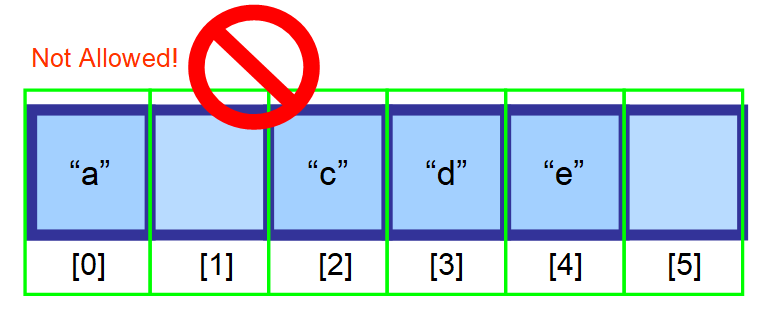
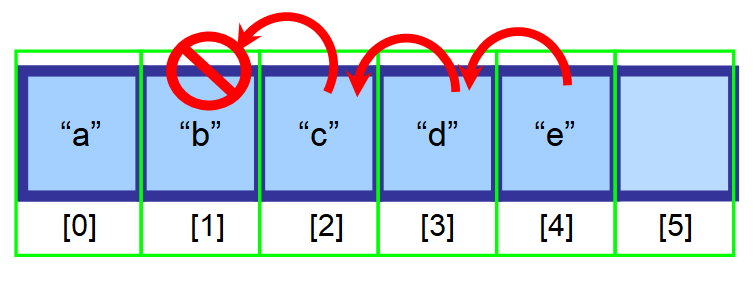
Prvky, které následují za prvkem, který chcete vymazat, byste měli přesunout o jeden index doleva.

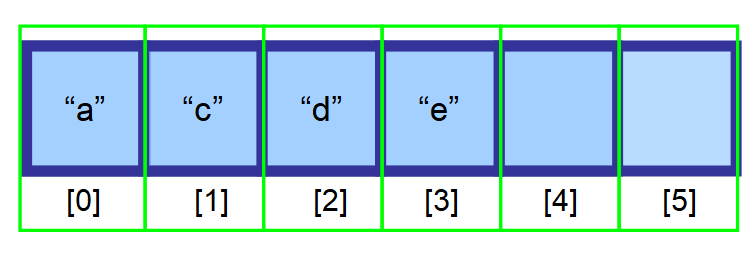
A nakonec máte toto výsledné pole 👇. Jak vidíte, prvek „b“ byl úspěšně odstraněn.

💡 Poznámka: Odstranění je velmi efektivní, pokud odstraníte poslední prvek. Protože je třeba vytvořit proměnnou pro sledování posledního indexu, který obsahuje prvky (ve výše uvedeném diagramu index 3), můžete tento prvek přímo odstranit pomocí indexu.

3️⃣ Vyhledání prvku

Pro vyhledání prvku v poli máte tři možnosti:

• Pokud víte, kde se nachází, použijte index.
• Pokud nevíte, kde se nachází, a vaše data jsou setříděná, můžete použít algoritmy pro optimalizaci vyhledávání, například binární vyhledávání.
• Pokud nevíte, kde se nachází, a vaše data nejsou setříděná, budete muset prohledat každý prvek v poli a zkontrolovat, zda je aktuální prvek hledaným prvkem (viz posloupnost diagramů níže).

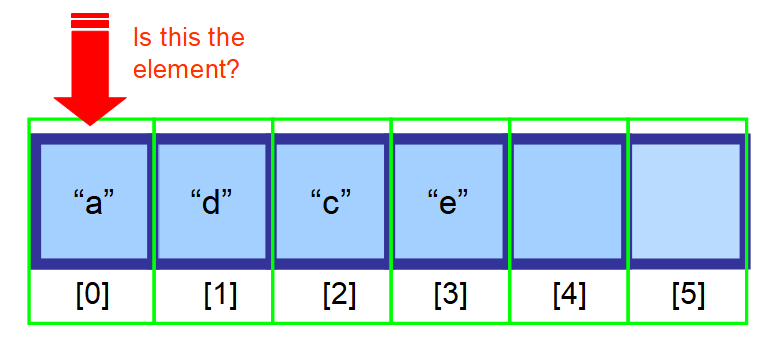
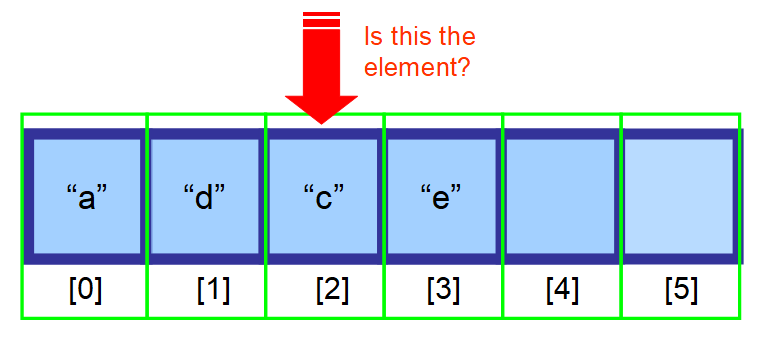
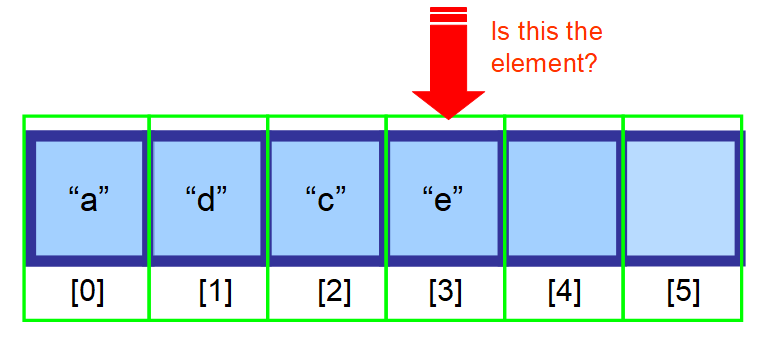
👋 Shrnutí…

• Pole jsou mimořádně výkonné datové struktury, které uchovávají prvky stejného typu. Typ prvků a velikost pole jsou pevně stanoveny a definovány při jeho vytvoření.
• Paměť je alokována ihned po vytvoření pole a je prázdná, dokud nepřiřadíte hodnoty.
• Prvky jsou umístěny na souvislých místech v paměti, takže k nim lze přistupovat velmi efektivně (náhodný přístup, O(1) = konstantní čas) pomocí indexů.
• Indexy začínají od 0, ne od 1, jak jsme zvyklí.
• Vkládání prvků na začátek nebo doprostřed pole zahrnuje přesun prvků doprava. Pokud je pole plné, vytvoří se nové, větší pole (což není příliš efektivní). Vložení na konec pole je velmi efektivní, konstantní čas O(1).
• Odstranění prvků ze začátku nebo ze středu pole zahrnuje přesunutí všech prvků doleva, aby v paměti nezůstalo prázdné místo. Tím je zaručeno, že prvky jsou uloženy v souvislých místech v paměti. Odstranění na konci pole je velmi efektivní, protože odstraníte pouze poslední prvek.
• Chcete-li najít prvek, musíte prohledat celé pole, dokud ho nenajdete. Pokud jsou data setříděná, můžete k optimalizaci procesu použít algoritmy, jako je binární vyhledávání.

„Uč se ze včerejška, žij pro dnešek, doufej v zítřek. Důležité je nepřestat se ptát.“
– Albert Einstein

👋 Děkuji vám!“

Pravdu doufám, že se vám můj článek líbil. ❤️
Sledujte mě na Twitteru, kde najdete další podobné články. 😃