Konstantní zrychlení
Analýza dvourozměrného pohybu projektilu se provádí rozdělením na dva pohyby: podél vodorovné a svislé osy.
Cíle učení
Analýza dvourozměrného pohybu projektilu podél vodorovné a svislé osy
Klíčové poznatky
Klíčové body
- Konstantní zrychlení při dvourozměrném pohybu má obecně podobu projektilu.
- Projektilní pohyb je pohyb předmětu vrženého nebo vymrštěného do vzduchu, na který působí pouze (svislé) tíhové zrychlení.
- Dvourozměrný projektilní pohyb analyzujeme tak, že jej rozložíme na dva nezávislé jednorozměrné pohyby podél svislé a vodorovné osy.
Klíčové pojmy
- kinematický: z pohybu nebo týkající se pohybu nebo kinematiky
Projekční pohyb je pohyb předmětu vrženého nebo vymrštěného do vzduchu, na který působí pouze gravitační síla. Objekt se nazývá projektil a jeho dráha se nazývá trajektorie. Pohyb padajících předmětů je jednoduchým jednorozměrným typem pohybu projektilu, při kterém nedochází k horizontálnímu pohybu. U dvourozměrného pohybu projektilu, jako je pohyb fotbalového míče nebo jiného hozeného předmětu, existuje jak vertikální, tak horizontální složka pohybu.
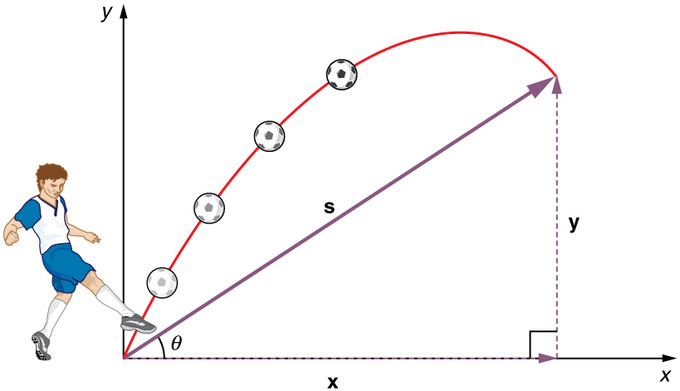
Projekční pohyb: Při házení kamenem nebo kopání do míče obecně vzniká vrhací pohyb, který má jak svislou, tak vodorovnou složku.
Nejdůležitějším faktem, který je třeba si zapamatovat, je, že pohyb podél kolmých os je nezávislý, a proto jej lze analyzovat samostatně. Klíčem k analýze dvourozměrného pohybu projektilu je rozdělit jej na dva pohyby, jeden podél vodorovné osy a druhý podél svislé. Abychom mohli popsat pohyb, musíme se zabývat rychlostí a zrychlením a také posunem.
Předpokládáme, že všechny síly kromě gravitační (jako je například odpor vzduchu a tření) jsou zanedbatelné. Složky zrychlení jsou pak velmi jednoduché: \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (předpokládáme, že k pohybu dochází v dostatečně malých výškách u povrchu Země, takže gravitační zrychlení je konstantní). Protože gravitační zrychlení působí pouze ve svislém směru, je \text{a}_\text{x} = 0. Lze tedy použít kinematické rovnice popisující pohyb ve směru \text{x}, respektive \text{y}:
\text{x} = \text{x}_0 + \text{v}_\text{x}. \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Dvourozměrný pohyb projektilu analyzujeme tak, že jej rozložíme na dva nezávislé jednorozměrné pohyby podél svislé a vodorovné osy. Horizontální pohyb je jednoduchý, protože \text{a}_\text{x} = 0 a \text{v}_\text{x} je tedy konstantní. Rychlost ve svislém směru začíná klesat, jak objekt stoupá; v nejvyšším bodě je svislá rychlost nulová. Když objekt opět klesá směrem k Zemi, vertikální rychlost se opět zvětšuje, ale směřuje opačným směrem než počáteční vertikální rychlost. Pohyby \text{x} a \text{y} lze překombinovat a získat tak celkovou rychlost v daném bodě trajektorie.
.
