
Pitagora din Samos (c.570-495) î.Hr.)
Biografie – Cine a fost Pitagora
Se afirmă uneori că datorăm matematica pură lui Pitagora, iar el este adesea numit primul matematician „adevărat”. Dar, deși contribuția sa a fost în mod clar importantă, el rămâne totuși o figură controversată.
Nu a lăsat el însuși nicio scriere matematică, iar mare parte din ceea ce știm despre gândirea pitagoreică ne vine din scrierile lui Philolaus și ale altor învățați pitagoreici de mai târziu. Într-adevăr, nu este deloc clar dacă multe (sau chiar niciuna) dintre teoremele atribuite lui Pitagora au fost de fapt rezolvate de Pitagora personal sau de adepții săi.
Școala pe care a înființat-o la Croton, în sudul Italiei, în jurul anului 530 î.Hr. a fost nucleul unei secte pitagoreice destul de bizare. Deși gândirea pitagoreică era dominată în mare măsură de matematică, ea era, de asemenea, profund mistică, iar Pitagora a impus filozofiile sale cvasi-religioase, vegetarianismul strict, viața în comun, riturile secrete și regulile sale ciudate tuturor membrilor școlii sale (inclusiv edicte bizare și aparent aleatorii despre a nu urina niciodată spre soare, a nu se căsători niciodată cu o femeie care poartă bijuterii de aur, a nu trece niciodată pe lângă un măgar întins pe stradă, a nu mânca și nici măcar a nu atinge fasolea fava neagră, etc) .
Membrii erau împărțiți în „mathematikoi” (sau „învățăcei”), care extindeau și dezvoltau munca mai mult matematică și științifică pe care Pitagora însuși a început-o, și „akousmatikoi” (sau „ascultători”), care se concentrau pe aspectele mai religioase și ritualice ale învățăturilor sale. Între cele două grupuri a existat întotdeauna o oarecare fricțiune și, în cele din urmă, secta a fost prinsă în niște lupte locale acerbe și, în cele din urmă, s-a dispersat. A crescut resentimentul față de caracterul secret și exclusivist al pitagorienilor și, în anul 460 î.Hr., toate locurile lor de întâlnire au fost arse și distruse, cel puțin 50 de membri fiind uciși numai în Croton.
Dictonul dominant al școlii lui Pitagora era „Totul este număr” sau „Dumnezeu este număr”, iar pitagorienii practicau efectiv un fel de numerologie sau cultul numerelor și considerau că fiecare număr are propriul caracter și semnificație. De exemplu, numărul unu era generatorul tuturor numerelor; doi reprezenta opinia; trei, armonia; patru, dreptatea; cinci, căsătoria; șase, creația; șapte, cele șapte planete sau „stelele rătăcitoare”; etc. Numerele impare erau considerate ca fiind feminine, iar cele pare ca fiind masculine.
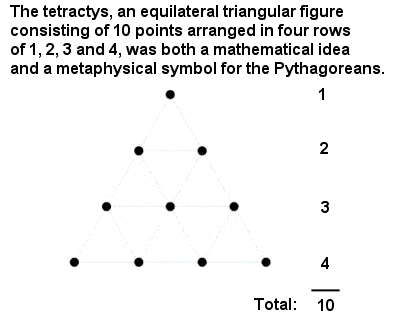
Tetractys pitagoreic
Cel mai sfânt număr dintre toate era „Tetractys” sau zece, un număr triunghiular compus din suma lui unu, doi, trei și patru. Este un mare omagiu adus realizărilor intelectuale ale pitagoreicilor faptul că au dedus locul special al numărului 10 dintr-un argument matematic abstract, mai degrabă decât din ceva atât de banal precum numărarea degetelor de la două mâini.
Cu toate acestea, Pitagora și școala sa – precum și o mână de alți matematicieni din Grecia antică – a fost în mare măsură responsabil pentru introducerea unei matematici mai riguroase decât ceea ce se întâmplase înainte, construind de la primele principii folosind axiome și logică. Înainte de Pitagora, de exemplu, geometria fusese doar o colecție de reguli derivate din măsurători empirice.
Pitagora a descoperit că se putea construi un sistem complet de matematică, în care elementele geometrice corespundeau cu numere și în care numerele întregi și raporturile lor erau tot ce era necesar pentru a stabili un întreg sistem de logică și adevăr.
Teorema lui Pitagora
Este amintit în principal pentru ceea ce a devenit cunoscut sub numele de Teorema lui Pitagora (sau Teorema lui Pitagora): că, pentru orice triunghi dreptunghic, pătratul lungimii ipotenuzei (cea mai lungă latură, opusă unghiului drept) este egal cu suma pătratelor celorlalte două laturi (sau „picioare”).
Scrisă sub forma unei ecuații: a2 + b2 = c2.
Ceea ce Pitagora și adepții săi nu au realizat este că acest lucru funcționează și pentru orice formă: astfel, aria unui pentagon de pe ipotenuză este egală cu suma pentagonelor de pe celelalte două laturi, la fel ca și în cazul unui semicerc sau al oricărei alte forme regulate (sau chiar neregulate(.
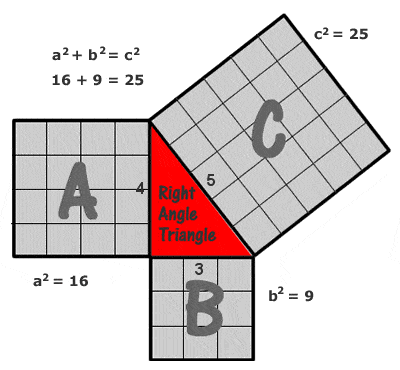
Teorema lui Pitagora (Pitagora)
Cel mai simplu și cel mai des citat exemplu de triunghi pitagoreic este cel cu laturile de 3, 4 și 5 unități (32 + 42 = 52, după cum se poate vedea desenând o grilă de pătrate de unități pe fiecare latură, ca în diagrama din dreapta), dar există un număr potențial infinit de alte „triple pitagoreice” cu numere întregi, începând cu (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. Trebuie remarcat, totuși, că (6, 8, 10) nu este ceea ce se numește o triplă pitagoreică „primitivă”, deoarece este doar un multiplu al lui (3, 4, 5).
Teorema lui Pitagora și proprietățile triunghiurilor dreptunghice pare să fie cea mai veche și mai răspândită dezvoltare matematică după aritmetica și geometria de bază, fiind abordată în unele dintre cele mai vechi texte matematice din Babilon și Egipt, datând de peste o mie de ani. Una dintre cele mai simple demonstrații provine din China antică și datează probabil cu mult înainte de nașterea lui Pitagora. Cu toate acestea, Pitagora a fost cel care a dat teoremei forma sa definitivă, deși nu este clar dacă Pitagora însuși a demonstrat-o definitiv sau doar a descris-o. Oricum ar fi, ea a devenit una dintre cele mai cunoscute teoreme matematice, existând în prezent până la 400 de demonstrații diferite, unele geometrice, altele algebrice, unele implicând ecuații diferențiale avansate etc.
A devenit însă curând evident că sunt posibile și soluții neintegrale, astfel încât un triunghi isoscel cu laturile 1, 1 și √2, de exemplu, are și un unghi drept, așa cum descoperiseră babilonienii cu secole înainte. Cu toate acestea, atunci când Hippasus, elevul lui Pitagora, a încercat să calculeze valoarea lui √2, a constatat că nu era posibil să o exprime sub formă de fracție, indicând astfel existența potențială a unei lumi cu totul noi de numere, numerele iraționale (numere care nu pot fi exprimate ca fracții simple de numere întregi). Această descoperire a spulberat mai degrabă lumea matematică elegantă construită de Pitagora și de adepții săi, iar existența unui număr care nu putea fi exprimat ca raport între două dintre creațiile lui Dumnezeu (care este modul în care ei gândeau despre numerele întregi) a pus în pericol întregul sistem de credință al cultului.
Primarul Hippasus a fost aparent înecat de către pitagorienii secretoși pentru că a difuzat această descoperire importantă în lumea exterioară. Dar înlocuirea ideii de divinitate a numerelor întregi cu conceptul mai bogat de continuum, a fost o evoluție esențială în matematică. Ea a marcat adevărata naștere a geometriei grecești, care se ocupă de linii, planuri și unghiuri, toate acestea fiind continue și nu discrete.
Printre alte realizări ale sale în geometrie, Pitagora (sau cel puțin urmașii săi, pitagorienii) a realizat și faptul că suma unghiurilor unui triunghi este egală cu două unghiuri drepte (180°) și, probabil, și generalizarea care afirmă că suma unghiurilor interioare ale unui poligon cu n laturi este egală cu (2n – 4) unghiuri drepte, iar suma unghiurilor sale exterioare este egală cu 4 unghiuri drepte. Ei au fost capabili să construiască figuri cu o anumită arie și să folosească algebra geometrică simplă, de exemplu să rezolve ecuații precum a(a – x) = x2 prin mijloace geometrice.
Pitagorienii au pus, de asemenea, bazele teoriei numerelor, cu cercetările lor asupra numerelor triunghiulare, pătrate și, de asemenea, perfecte (numere care sunt suma divizorilor lor). Ei au descoperit câteva proprietăți noi ale numerelor pătrate, cum ar fi faptul că pătratul unui număr n este egal cu suma primelor n numere impare (de exemplu, 42 = 16 = 1 + 3 + 5 + 7). De asemenea, au descoperit cel puțin prima pereche de numere amiabile, 220 și 284 (numerele amiabile sunt perechi de numere pentru care suma divizorilor unui număr este egală cu celălalt număr; de exemplu, divizorii proprii ai lui 220 sunt 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 și 110, a căror sumă este 284; iar divizorii proprii ai lui 284 sunt 1, 2, 4, 71 și 142, a căror sumă este 220).
Teorie muzicală
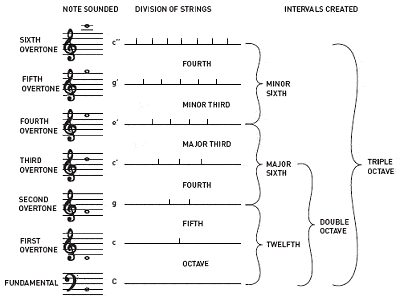
Pitagora este creditat cu descoperirea rapoartelor dintre tonurile muzicale armonioase
Pitagora este creditat și cu descoperirea faptului că intervalele dintre notele muzicale armonioase au întotdeauna rapoarte de numere întregi. De exemplu, dacă se cântă o jumătate de lungime a unei coarde de chitară se obține aceeași notă ca și coarda deschisă, dar cu o octavă mai sus; o treime de lungime dă o notă diferită, dar armonioasă; etc.
Pe de altă parte, raporturile care nu sunt numere întregi au tendința de a da sunete disonante. În acest fel, Pitagora a descris primele patru supratonuri care creează intervalele comune care au devenit elementele de bază ale armoniei muzicale: octava (1:1), cvintă perfectă (3:2), cvartă perfectă (4:3) și terță majoră (5:4). Cel mai vechi mod de acordaj al scalei cromatice de 12 note este cunoscut sub numele de acordaj pitagoreic și se bazează pe un teanc de cvinte perfecte, fiecare acordată în raportul 3:2.
Misticul Pitagora a fost atât de entuziasmat de această descoperire încât a fost convins că întregul univers se bazează pe numere și că planetele și stelele se mișcă în conformitate cu ecuații matematice, care corespund notelor muzicale, producând astfel un fel de simfonie, „Musical Universalis” sau „Muzica Sferelor”.
| << Înapoi la Matematica greacă | Înapoi la Platon >> |
.
