Știm cum să găsim rădăcina pătrată a oricărui număr real pozitiv. În mod similar, putem găsi rădăcina pătrată a unui număr negativ. Diferența constă în faptul că rădăcina nu este reală. Dacă valoarea din radicand este negativă, se spune că rădăcina este un număr imaginar. Numărul imaginar i este definit ca fiind rădăcina pătrată a lui 1 negativ.
Atunci, folosind proprietățile radicalilor,
Potem scrie rădăcina pătrată a oricărui număr negativ ca multiplu al lui i. Să luăm în considerare rădăcina pătrată a lui -25.
Utilizăm 5i și nu -\text{5}i\\\ deoarece rădăcina principală a lui 25 este rădăcina pozitivă.
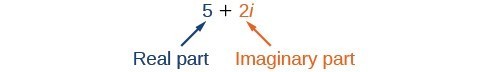
Figura 1
Un număr complex este suma unui număr real și a unui număr imaginar. Un număr complex se exprimă în formă standard când se scrie a + bi unde a este partea reală și bi este partea imaginară. De exemplu, 5+2i\\\\ este un număr complex. La fel este și 3+4\sqrt{3}i\\\\.
Numerele imaginare se disting de numerele reale deoarece un număr imaginar la pătrat produce un număr real negativ. Reamintim că, atunci când un număr real pozitiv este ridicat la pătrat, rezultatul este un număr real pozitiv, iar atunci când un număr real negativ este ridicat la pătrat, din nou, rezultatul este un număr real pozitiv. Numerele complexe sunt o combinație de numere reale și numere imaginare.
O notă generală: Numere imaginare și complexe
Un număr complex este un număr de forma a+bi\\\ unde
- a este partea reală a numărului complex.
- bi este partea imaginară a numărului complex.
Dacă b=0\\\\, atunci a+bi\\\\ este un număr real. Dacă a=0\\\ și b nu este egal cu 0, numărul complex se numește număr imaginar. Un număr imaginar este o rădăcină pară a unui număr negativ.
Cum se procedează: Dat fiind un număr imaginar, exprimați-l în formă standard.
- Scrieți \sqrt{-a}\\\ sub forma \sqrt{a}\sqrt{-1}\\\\\.
- Exprimați \sqrt{-1}\\\ sub forma i.
- Scrieți \sqrt{a}\cdot i\\ sub forma cea mai simplă.
Exemplul 1: Exprimarea unui număr imaginar în forma standard
Exprimați \sqrt{-9}\\ sub forma standard.
Soluție
\sqrt{-9}=\sqrt{9}\sqrt{-1}=3i\\\
În forma standard, acesta este 0+3i\\\.
Încercați 1
Exprimați \sqrt{-24}\\ în forma standard.
Soluția
.
