În această secțiune, ne vom familiariza cu operațiile și notațiile cu seturi, astfel încât să putem aplica aceste concepte atât la probleme de numărare, cât și de probabilitate. Începem prin a defini câțiva termeni.
Un set este o colecție de obiecte, iar membrii săi se numesc elemente ale setului. Numim setul folosind litere majuscule, iar membrii săi îi cuprindem între paranteze curbe. Să presupunem că trebuie să enumerăm membrii clubului de șah. Folosim următoarea notație a seturilor.
C ={Ken, Bob, Tran, Shanti, Eric}
Un set care nu are membri se numește set gol. Setul gol este notat cu simbolul Ø.
Două seturi sunt egale dacă au aceleași elemente.
Un set A este un subset al unui set B dacă fiecare membru al lui A este, de asemenea, membru al lui B.
Supunem că C = {Al, Bob, Chris, David, Ed} și A = {Bob, David}. Atunci A este un subansamblu al lui C, scris ca 
.
Care ansamblu este un subansamblu al lui însuși, iar ansamblul gol este un subansamblu al oricărui ansamblu.
Unirea a două ansambluri
După ce A și B sunt două ansambluri, atunci uniunea lui A și B, scrisă ca 
, este ansamblul tuturor elementelor care sunt fie în A, fie în B, fie în ambele A și B.
Intersecția a două ansambluri
Să fie A și B două ansambluri, atunci intersecția lui A și B, scrisă sub forma 
, este ansamblul tuturor elementelor care sunt comune ambelor ansambluri A și B.
Un ansamblu universal U este ansamblul format din toate elementele luate în considerare.
Complementul unui ansamblu
Dacă A este un ansamblu oarecare, atunci complementul ansamblului A, scris cu 
, este ansamblul format din elementele din ansamblul universal U care nu se află în A.
Seturi disjuncte
Două seturi A și B se numesc seturi disjuncte dacă intersecția lor este un set gol.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {portocaliu, verde, indigo, violet}Pentru a obține o mai bună înțelegere, să presupunem că ansamblul universal U reprezintă culorile din spectru, iar P culorile primare, atunci reprezintă acele culori din spectru care nu sunt culori primare.
.
= {roșu, galben, albastru, verde}
= {oranj, indigo, violet}
= {roșu, galben, albastru, violet} = {violet}Diagrame Venn
Acum vom folosi diagramele Venn pentru a ilustra relațiile dintre seturi. La sfârșitul anilor 1800, un logician englez pe nume John Venn a dezvoltat o metodă de reprezentare a relațiilor dintre seturi. El a reprezentat aceste relații folosind diagrame, care sunt cunoscute acum sub numele de diagrame Venn. O diagramă Venn reprezintă un set ca interiorul unui cerc. Adesea, două sau mai multe cercuri sunt închise într-un dreptunghi în care dreptunghiul reprezintă setul universal. Pentru a vizualiza o intersecție sau o uniune a unui set este ușor de vizualizat. În această secțiune, vom folosi în principal diagramele Venn pentru a sorta diverse populații și pentru a număra obiecte.
|
(a) |
(b) |
(c) |
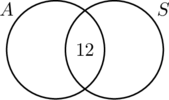
Pentru că 30 de persoane conduceau mașini cu transmisie automată, cercul A trebuie să conțină 30 de elemente. Aceasta înseamnă că x + 12 = 30, sau x = 18. În mod similar, deoarece 20 de persoane au condus mașini cu transmisie standard, cercul B trebuie să conțină 20 de elemente, sau y +12 = 20, ceea ce la rândul său face ca y = 8.
Acum că toate informațiile sunt ordonate, este ușor de citit din diagramă că 18 persoane au condus mașini doar cu transmisie automată, 12 persoane au condus ambele tipuri de mașini, iar 8 persoane au condus mașini doar cu transmisie standard. Prin urmare, 18 + 12 + 8 = 38 de persoane au participat la sondaj.
|
(a) |
(b) |
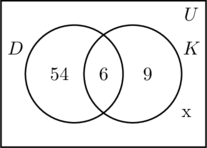
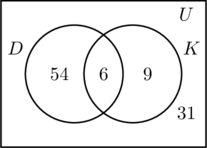
Completăm cele trei regiuni asociate cu seturile D și K în același mod ca înainte. Deoarece 100 de persoane au participat la sondaj, dreptunghiul care reprezintă ansamblul universal U trebuie să conțină 100 de obiecte. Fie ca x să reprezinte acele persoane din ansamblul universal care nu se află nici în ansamblul D, nici în K. Aceasta înseamnă că 54 + 6 + 6 + 9 + x = 100, sau x = 31.
Prin urmare, există 31 de persoane participante la sondaj care nu au vizitat niciun loc.
- 50 aleargă, 30 înoată și 35 merg pe bicicletă
- 14 aleargă și înoată
- 7 înoată și merge pe bicicletă
- 9 aleargă și merge pe bicicletă
- 3 persoane participă la toate cele trei activități
Soluție
|
(a) |
(b) |
(c) . |
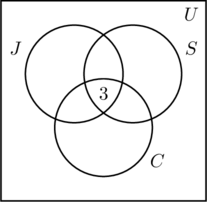
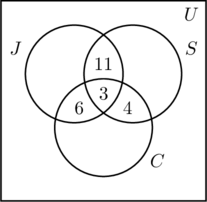
Punem un 3 în regiunea cea mai interioară a figurii (a) deoarece reprezintă numărul de persoane care participă la toate cele trei activități. În continuare calculăm x, y și z.
- Deoarece 14 persoane aleargă și înoată, x +3 = 14, sau x = 11.
- După faptul că 9 persoane aleargă și merg pe bicicletă rezultă y + 3 = 9, sau y = 6.
- Din moment ce 7 persoane înoată și merg cu bicicleta, z + 3 = 7, sau z = 4.
- Aceste informații sunt reprezentate în figura (b).
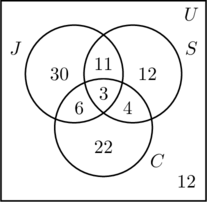
- Din moment ce 50 de persoane aleargă, m + 11 + 6 + 3 = 50, sau m = 30.
- 30 de persoane înoată, prin urmare, n + 11 + 4 + 3 = 30, sau n = 12.
- 35 de persoane merg cu bicicleta, prin urmare, p + 6 + 4 + 3 = 35, sau p = 22.
- Însumând toate intrările din cele trei seturi, obținem suma de 88. Deoarece au fost intervievate 100 de persoane, numărul din interiorul setului universal, dar din afara tuturor celor trei seturi este 100 – 88, sau 12.
- În figura (c), informațiile sunt ordonate, iar întrebările pot fi ușor de răspuns.
Întrebări practice
1. Fie setul universal U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, și W = {a, c, e, g, i}. Enumerați membrii următoarelor seturi:
a. 
b. 
2. Se consideră următoarele seturi: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Gripă, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, și C = {SARS, Listeria, Tuberculoză, H5N1, Salmonella, HIV, COVID-19}. Enumerați membrii următoarelor seturi:
a. 
b. 
3. Un sondaj efectuat în rândul sportivilor a arătat că, pentru durerile minore, 30 foloseau aspirină, 50 foloseau ibuprofen, iar 15 le foloseau pe amândouă. Toți sportivii chestionați au folosit cel puțin unul dintre cele două analgezice. Câți sportivi au fost intervievați?
4. Un studiu efectuat pe 150 de elevi de liceu a arătat că 25 au raportat că au suferit anterior o comoție sau un traumatism cranian, 52 au raportat că s-au confruntat cu boli psihice, iar 15 au raportat ambele rezultate. Câți elevi nu au raportat niciunul dintre rezultate?
5. Un sondaj efectuat în rândul a 100 de studenți de la Universitatea Ryerson a constatat că 50 sunt abonați la Netflix, 40 la Amazon Prime și 30 la Disney+. Dintre aceștia, 15 sunt abonați atât la Netflix, cât și la Amazon Prime, 10 atât la Amazon Prime, cât și la Disney+, 10 atât la Netflix, cât și la Disney+, iar 5 au toate cele trei servicii de abonament. Desenați o diagramă Venn și determinați următoarele:
a. Numărul de studenți care sunt abonați la Amazon Prime, dar nu și la celelalte două servicii de streaming.
b. Numărul de studenți abonați la Netflix sau Amazon Prime, dar nu și la Disney+.
c. Numărul de studenți care nu sunt abonați la niciunul dintre aceste servicii.
.