Un grup 
este un ansamblu finit sau infinit de elemente împreună cu o operație binară (numită operație de grup) care îndeplinesc împreună cele patru proprietăți fundamentale de închidere, asociativitate, proprietatea identității și proprietatea inversă. Operația în raport cu care se definește un grup este adesea numită „operație de grup”, iar despre un ansamblu se spune că este un grup „sub” această operație. Elementele 
, 
, 
, … cu operația binară între 
și 
notată 
formează un grup dacă
1. Închidere: Dacă 
și 
sunt două elemente în 
, atunci produsul 
este de asemenea în 
.
2. Asociativitate: Înmulțirea definită este asociativă, adică, pentru toate 
, 
.
3. Identitate: Există un element de identitate 
(cunoscut și ca 1, 
sau 
) astfel încât 
pentru fiecare element 
.
4. Inversa: Trebuie să existe un invers (alias reciproca) al fiecărui element. Prin urmare, pentru fiecare element 
din 
, setul conține un element 
astfel încât 
.
Un grup este un monoid, fiecare dintre elementele căruia este inversabil.
Un grup trebuie să conțină cel puțin un element, grupul unic (până la izomorfism) cu un singur element fiind cunoscut sub numele de grupul trivial.
Studiul grupurilor este cunoscut sub numele de teoria grupurilor. Dacă există un număr finit de elemente, grupul se numește grup finit, iar numărul de elemente se numește ordinul de grup al grupului. Un subansamblu al unui grup care este închis sub operația de grup și operația inversă se numește subgrup. Subgrupurile sunt, de asemenea, grupuri și multe grupuri întâlnite în mod obișnuit sunt, de fapt, subgrupuri speciale ale unui grup mai general mai mare.
Un exemplu de bază de grup finit este grupul simetric 
, care este grupul permutărilor (sau „sub permutare”) a 
obiecte. Cel mai simplu grup infinit este ansamblul numerelor întregi sub adunare obișnuită. Pentru grupurile continue, se pot lua în considerare numerele reale sau ansamblul matricelor 
inversabile. Aceste două din urmă sunt exemple de grupuri Lie.
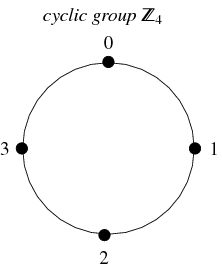
Un tip foarte comun de grup este reprezentat de grupurile ciclice. Acest grup este izomorf cu grupul numerelor întregi (modulo 
), se notează 
, 
sau 
și este definit pentru fiecare număr întreg 
. Este închis la adunare, asociativ și are inverse unice. Numerele de la 0 la 
reprezintă elementele sale, elementul identitate fiind reprezentat de 0, iar inversul lui 
este reprezentat de 
.
O hartă între două grupuri care păstrează identitatea și operația de grup se numește homomorfism. Dacă un homomorfism are un invers care este tot un homomorfism, atunci se numește izomorfism și cele două grupuri se numesc izomorfe. Două grupuri care sunt izomorfe unul față de celălalt sunt considerate „identice” atunci când sunt privite ca grupuri abstracte. De exemplu, grupul rotațiilor unui pătrat, ilustrat mai jos, este grupul ciclic 
.
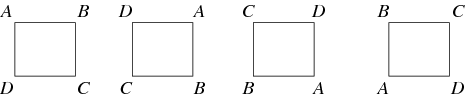
În general, o acțiune de grup este atunci când un grup acționează asupra unui ansamblu, permutându-i elementele, astfel încât harta de la grup la grupul de permutare al ansamblului să fie un homomorfism. De exemplu, rotațiile unui pătrat sunt un subgrup al permutărilor colțurilor sale. O acțiune de grup importantă pentru orice grup 
este acțiunea sa asupra lui însuși prin conjugare. Acestea sunt doar câteva dintre automorfismele de grup posibile. Un alt tip important de acțiune de grup este o reprezentare de grup, în care grupul acționează asupra unui spațiu vectorial prin intermediul unor hărți liniare inversabile. Atunci când câmpul spațiului vectorial este reprezentat de numerele complexe, uneori o reprezentare se numește modul CG.
Acțiunile de grup, și în special reprezentările, sunt foarte importante în aplicații, nu numai în teoria grupurilor, ci și în fizică și chimie. Deoarece un grup poate fi gândit ca un obiect matematic abstract, același grup poate apărea în contexte diferite. Prin urmare, este util să ne gândim la o reprezentare a grupului ca la o întruchipare particulară a grupului, care poate avea și alte reprezentări. O reprezentare ireductibilă a unui grup este o reprezentare pentru care nu există nicio transformare unitară care să transforme matricea de reprezentare în formă de diagonală bloc. Reprezentările ireductibile au o serie de proprietăți remarcabile, așa cum sunt formalizate în teorema ortogonalității grupului.
.