- Obiective de învățare
- Exemplu 1. Calcularea energiei fotonilor și a efectului fotoelectric: O lumină violetă
- Strategie
- Soluție pentru partea 1
- Soluția pentru partea 2
- Discuție
- Explorări PhET: Efectul fotoelectric
- Rezumat al secțiunii
- Întrebări conceptuale
- Probleme & Exerciții
- Glosar
- Soluții alese la probleme & Exerciții
Obiective de învățare
Până la sfârșitul acestei secțiuni, veți fi capabili să:
- Descrieți un experiment tipic de efect fotoelectric.
- Determinați energia cinetică maximă a fotoelectronilor ejectați de fotoni de o anumită energie sau lungime de undă, atunci când vi se dă energia cinetică maximă a fotoelectronilor pentru o energie sau o lungime de undă diferită a fotonilor.
Când lumina lovește materiale, poate ejecta electroni din acestea. Acest lucru se numește efect fotoelectric, ceea ce înseamnă că lumina (foto) produce electricitate. O utilizare obișnuită a efectului fotoelectric este în cazul aparatelor de măsurat lumina, cum ar fi cele care reglează diafragma automată la diferite tipuri de aparate foto. În mod similar, o altă utilizare este în cazul celulelor solare, așa cum probabil aveți în calculatorul dumneavoastră sau ați văzut pe un acoperiș sau pe un indicator rutier. Acestea se folosesc de efectul fotoelectric pentru a transforma lumina în energie electrică pentru funcționarea diferitelor dispozitive.

Figura 1. Efectul fotoelectric poate fi observat lăsând lumina să cadă pe placa metalică din acest tub vidat. Electronii ejectați de lumină sunt colectați pe firul colector și măsurați sub formă de curent. O tensiune de întârziere între firul colector și placă poate fi apoi reglată astfel încât să se determine energia electronilor ejectați. De exemplu, dacă este suficient de negativă, niciun electron nu va ajunge pe fir. (credit: P.P. Urone)
Acest efect este cunoscut de mai bine de un secol și poate fi studiat cu ajutorul unui dispozitiv precum cel prezentat în figura 1. Această figură prezintă un tub vidat cu o placă metalică și un fir colector care sunt conectate de o sursă de tensiune variabilă, cu colectorul mai negativ decât placa. Atunci când lumina (sau alte radiații EM) lovește placa din tubul vidat, aceasta poate ejecta electroni. În cazul în care electronii au o energie în electronvolți (eV) mai mare decât diferența de potențial dintre placă și firul în volți, unii electroni vor fi colectați pe fir. Deoarece energia electronilor în eV este eV, unde q este sarcina electronică și V este diferența de potențial, energia electronilor poate fi măsurată prin reglarea tensiunii de întârziere dintre fir și placă. Tensiunea care împiedică electronii să ajungă pe fir este egală cu energia în eV. De exemplu, dacă -3,00 V abia oprește electronii, energia lor este de 3,00 eV. Numărul de electroni expulzați poate fi determinat prin măsurarea curentului dintre fir și placă. Cu cât mai multă lumină, cu atât mai mulți electroni; un mic circuit permite ca acest dispozitiv să fie folosit ca un aparat de măsurat lumina.
Ceea ce este cu adevărat important despre efectul fotoelectric este ceea ce a dedus Albert Einstein din el. Einstein și-a dat seama că există câteva caracteristici ale efectului fotoelectric care pot fi explicate numai dacă radiația EM este ea însăși cuantificată: fluxul aparent continuu de energie dintr-o undă EM este de fapt compus din cuante de energie numite fotoni. În explicația sa privind efectul fotoelectric, Einstein a definit o unitate cuantificată sau o cuantă de energie EM, pe care noi o numim acum foton, cu o energie proporțională cu frecvența radiației EM. Sub formă de ecuație, energia fotonului este E = hf, unde E este energia unui foton de frecvență f și h este constanta lui Planck. Această idee revoluționară seamănă cu cuantificarea de către Planck a stărilor de energie în oscilațiile corpului negru, dar este foarte diferită. Este vorba de cuantificarea radiației EM în sine. Undele EM sunt compuse din fotoni și nu sunt unde netede și continue, așa cum au fost descrise în capitolele anterioare despre optică. Energia lor este absorbită și emisă în blocuri, nu continuu. Acest lucru este exact în concordanță cu cuantificarea de către Planck a nivelurilor de energie în oscilatoarele corpului negru, deoarece aceste oscilatoare își cresc și scad energia în trepte de hf prin absorbția și emiterea de fotoni având E = hf. Noi nu observăm acest lucru cu ochii noștri, deoarece există atât de mulți fotoni în sursele obișnuite de lumină încât fotonii individuali trec neobservați. (A se vedea figura 2.) Următoarea secțiune a textului (Energiile fotonice și spectrul electromagnetic) este dedicată unei discuții despre fotoni și despre unele dintre caracteristicile și implicațiile acestora. Deocamdată, vom folosi conceptul de foton pentru a explica efectul fotoelectric, așa cum a făcut Einstein.
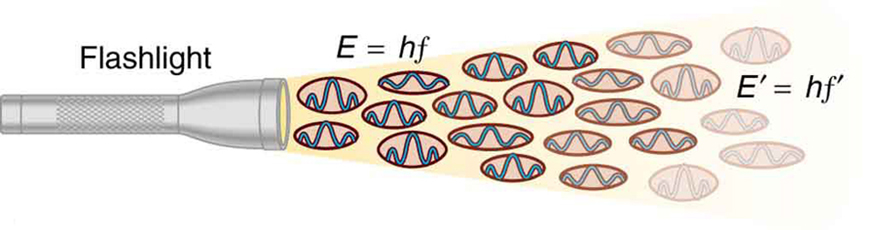
Figura 2. O undă EM de frecvență f este compusă din fotoni, sau cuante individuale de radiație EM. Energia fiecărui foton este E = hf, unde h este constanta lui Planck și f este frecvența radiației EM. O intensitate mai mare înseamnă mai mulți fotoni pe unitatea de suprafață. Lanterna emite un număr mare de fotoni de mai multe frecvențe diferite, prin urmare alții au energia E′ = hf′, și așa mai departe.
Efectul fotoelectric are proprietățile discutate mai jos. Toate aceste proprietăți sunt în concordanță cu ideea că fotonii individuali ai radiației EM sunt absorbiți de electronii individuali dintr-un material, electronul căpătând energia fotonului. Unele dintre aceste proprietăți nu sunt în concordanță cu ideea că radiația EM este o undă simplă. Pentru simplificare, să luăm în considerare ce se întâmplă cu radiația EM monocromatică în care toți fotonii au aceeași energie hf.
- Dacă variem frecvența radiației EM care cade pe un material, constatăm următoarele: Pentru un anumit material, există o frecvență de prag f0 pentru radiația EM sub care nu sunt expulzați electroni, indiferent de intensitate. Fotonii individuali interacționează cu electronii individuali. Astfel, dacă energia fotonului este prea mică pentru a desprinde un electron, niciun electron nu va fi expulzat. Dacă radiația EM ar fi o simplă undă, s-ar putea obține suficientă energie prin creșterea intensității.
- Odată ce radiația EM cade pe un material, electronii sunt ejectați fără întârziere. De îndată ce un foton individual de o frecvență suficient de mare este absorbit de un electron individual, electronul este ejectat. Dacă radiația EM ar fi o simplă undă, ar fi necesare câteva minute pentru ca pe suprafața metalului să se depună suficientă energie pentru a ejecta un electron.
- Numărul de electroni ejectați pe unitate de timp este proporțional cu intensitatea radiației EM și cu nicio altă caracteristică. Radiația EM de intensitate mare constă dintr-un număr mare de fotoni pe unitatea de suprafață, toți fotonii având aceeași energie caracteristică hf.
- Dacă variem intensitatea radiației EM și măsurăm energia electronilor ejectați, vom găsi următoarele: Energia cinetică maximă a electronilor ejectați este independentă de intensitatea radiației EM. Deoarece există atât de mulți electroni într-un material, este extrem de puțin probabil ca doi fotoni să interacționeze cu același electron în același timp, crescând astfel energia dată acestuia. În schimb (așa cum s-a menționat la punctul 3 de mai sus), creșterea intensității are ca rezultat mai mulți electroni de aceeași energie care sunt ejectați. Dacă radiația EM ar fi o undă simplă, o intensitate mai mare ar putea da mai multă energie, iar electronii cu energie mai mare ar fi ejectați.
- Energia cinetică a unui electron ejectat este egală cu energia fotonului minus energia de legătură a electronului în materialul specific. Un foton individual poate da toată energia sa unui electron. Energia fotonului este parțial utilizată pentru a rupe electronul din material. Restul intră în energia cinetică a electronului ejectat. În formă de ecuație, aceasta este dată de KEe = hf – BE, unde KEe este energia cinetică maximă a electronului ejectat, hf este energia fotonului, iar BE este energia de legătură a electronului cu materialul respectiv. (BE este uneori numită funcția de lucru a materialului.) Această ecuație, datorată lui Einstein în 1905, explică cantitativ proprietățile efectului fotoelectric. Un foton individual de radiație EM (nu vine altfel) interacționează cu un electron individual, furnizând suficientă energie, BE, pentru a-l desprinde, iar restul se transformă în energie cinetică. Energia de legătură este BE = hf0, unde f0 este frecvența de prag pentru materialul respectiv. Figura 3 prezintă un grafic al valorii maxime a KEe în funcție de frecvența radiației EM incidente care cade pe un anumit material.
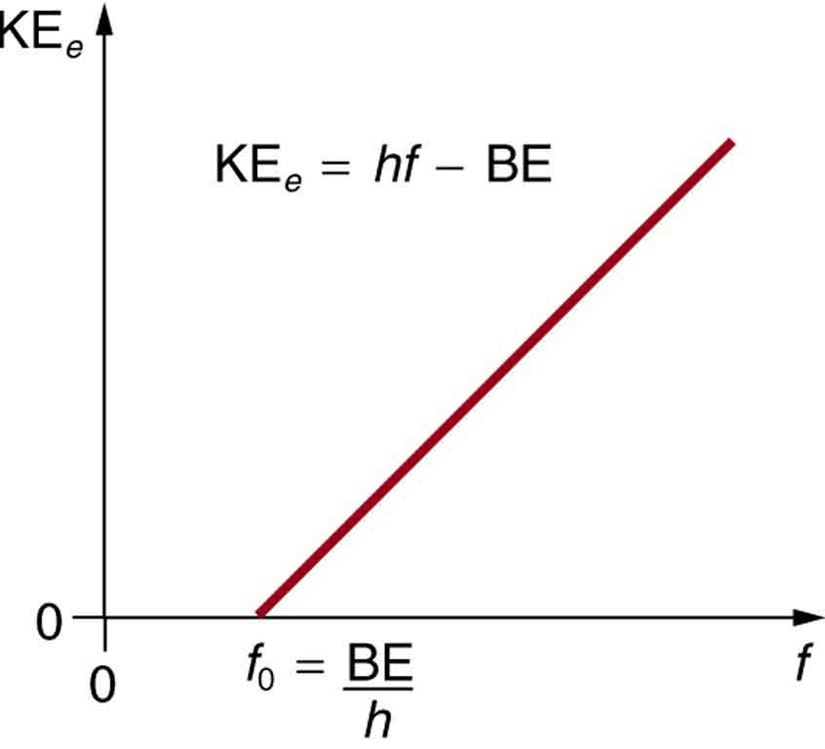
Figura 3. Efectul fotoelectric. Graficul energiei cinetice a unui electron ejectat, KEe, în funcție de frecvența radiației EM care cade pe un anumit material. Există o frecvență de prag sub care niciun electron nu este ejectat, deoarece fotonul individual care interacționează cu un electron individual nu are suficientă energie pentru a-l desprinde. Peste energia de prag, KEe crește liniar cu f, în concordanță cu KEe = hf – BE. Panta acestei drepte este h – datele pot fi utilizate pentru a determina experimental constanta lui Planck. Einstein a dat prima explicație reușită a acestor date, propunând ideea de fotoni – cuante de radiație EM.
Ideea lui Einstein că radiația EM este cuantificată a fost crucială pentru începuturile mecanicii cuantice. Este un concept mult mai general decât ar putea implica explicația sa asupra efectului fotoelectric. Toată radiația EM poate fi, de asemenea, modelată sub formă de fotoni, iar caracteristicile radiației EM sunt în întregime în concordanță cu acest fapt. (După cum vom vedea în secțiunea următoare, multe aspecte ale radiației EM, cum ar fi pericolele pe care le prezintă radiația ultravioletă (UV), pot fi explicate doar prin proprietățile fotonilor). Mai faimos pentru relativitatea modernă, Einstein a plantat o sămânță importantă pentru mecanica cuantică în 1905, în același an în care a publicat prima sa lucrare despre relativitatea specială. Explicația sa privind efectul fotoelectric a stat la baza Premiului Nobel care i-a fost acordat în 1921. Deși alte contribuții ale sale la fizica teoretică au fost, de asemenea, remarcate în cadrul acelui premiu, relativitatea specială și generală nu au fost recunoscute pe deplin, în ciuda faptului că au fost parțial verificate prin experiment până în 1921. Deși venerat ca erou, acest mare om nu a primit niciodată recunoașterea Nobel pentru cea mai faimoasă lucrare a sa – relativitatea.
Exemplu 1. Calcularea energiei fotonilor și a efectului fotoelectric: O lumină violetă
1. Care este energia în jouli și electroni-volți a unui foton de lumină violetă de 420 nm?
2. Care este energia cinetică maximă a electronilor ejectați din calciu de lumina violetă de 420 nm, având în vedere că energia de legătură (sau funcția de lucru) a electronilor pentru calciul metalic este de 2,71 eV?
Strategie
Pentru a rezolva partea 1, rețineți că energia unui foton este dată de E = hf. Pentru partea 2, odată calculată energia fotonului, este o aplicație directă a formulei KEe = hf – BE pentru a găsi energia cinetică maximă a electronului ejectat, deoarece BE este dată.
Soluție pentru partea 1
Energia fotonului este dată de E = hf.
Din moment ce ne este dată lungimea de undă și nu frecvența, rezolvăm relația familiară c = fλ pentru frecvență, obținând f=\frac{c}{\lambda}\\\\.
Combinând aceste două ecuații se obține relația utilă E=\frac{hc}{\lambda}\\\\.
Înlocuind acum valorile cunoscute rezultă
\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4.74\times10^{-19}\text{ J}\\
Convertind în eV, energia fotonului este
\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}{1,6\times10^{-19}\text{ J}}=2,96\text{ eV}\\\
Soluția pentru partea 2
Căutarea energiei cinetice a electronului ejectat este acum o simplă aplicare a ecuației KEe = hf – BE. Înlocuind energia fotonului și energia de legătură se obține KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Discuție
Energia acestui foton de lumină violetă de 420 nm este o fracțiune minusculă de joule și, prin urmare, nu este de mirare că un singur foton ar fi dificil de perceput direct de către noi – oamenii sunt mai mult adaptați la energii de ordinul joulelor. Dar dacă ne uităm la energia în electronvolți, putem vedea că acest foton are suficientă energie pentru a afecta atomii și moleculele. O moleculă de ADN poate fi ruptă cu aproximativ 1 eV de energie, de exemplu, iar energiile atomice și moleculare tipice sunt de ordinul eV, astfel încât fotonul UV din acest exemplu ar putea avea efecte biologice. Electronul ejectat (numit fotoelectron) are o energie destul de mică și nu ar călători prea departe, cu excepția vidului. Electronul ar fi oprit de un potențial de întârziere de numai 0,26 eV. De fapt, dacă lungimea de undă a fotonului ar fi mai mare, iar energia sa ar fi mai mică de 2,71 eV, atunci formula ar da o energie cinetică negativă, ceea ce este imposibil. Acest lucru înseamnă pur și simplu că fotonii de 420 nm, cu energia lor de 2,96 eV, nu sunt cu mult peste pragul de frecvență. Puteți demonstra singuri că lungimea de undă de prag este de 459 nm (lumină albastră). Acest lucru înseamnă că, dacă calciul metalic este utilizat într-un contor de lumină, contorul va fi insensibil la lungimi de undă mai mari decât cele ale luminii albastre. Un astfel de contor de lumină ar fi complet insensibil la lumina roșie, de exemplu.
Explorări PhET: Efectul fotoelectric
Vezi cum lumina izbește electronii de pe o țintă metalică și recreezi experimentul care a dat naștere domeniului mecanicii cuantice.

Click pentru a descărca simularea. Rulați folosind Java.
Rezumat al secțiunii
- Efectul fotoelectric este procesul prin care radiația EM ejectează electroni dintr-un material.
- Einstein a propus ca fotonii să fie cuante de radiație EM având energia E = hf, unde f este frecvența radiației.
- Toată radiația EM este compusă din fotoni. După cum a explicat Einstein, toate caracteristicile efectului fotoelectric se datorează interacțiunii fotonilor individuali cu electronii individuali.
- Energia cinetică maximă KEe a electronilor ejectați (fotoelectroni) este dată de KEe = hf – BE, unde hf este energia fotonului și BE este energia de legătură (sau funcția de lucru) a electronului cu materialul respectiv.
Întrebări conceptuale
- Este lumina vizibilă singurul tip de radiație EM care poate provoca efectul fotoelectric?
- Ce aspecte ale efectului fotoelectric nu pot fi explicate fără fotoni? Care pot fi explicate fără fotoni? Sunt acestea din urmă incompatibile cu existența fotonilor?
- Efectul fotoelectric este o consecință directă a caracterului ondulatoriu al radiației EM sau a caracterului de particulă al radiației EM? Explicați pe scurt.
- Insulatorii (nemetalii) au un BE mai mare decât metalele și este mai dificil pentru fotoni să ejecteze electroni din izolatori. Discutați cum se leagă acest lucru de sarcinile libere din metale care le fac bune conductoare.
- Dacă ridicați și scuturați o bucată de metal care are în ea electroni liberi să se deplaseze sub formă de curent, niciun electron nu cade afară. Totuși, dacă încălziți metalul, electronii pot fi scoși prin fierbere. Explicați aceste două fapte în ceea ce privește cantitatea și distribuția energiei implicate de scuturarea obiectului în comparație cu încălzirea acestuia.
Probleme & Exerciții
- Care este cea mai mare lungime de undă a radiației EM care poate ejecta un fotoelectron din argint, având în vedere că energia de legătură este de 4,73 eV? Este aceasta în domeniul vizibil?
- Căutați cea mai mare lungime de undă a fotonului care poate ejecta un electron din potasiu, având în vedere că energia de legătură este de 2,24 eV. Este aceasta o radiație EM vizibilă?
- Care este energia de legătură în eV a electronilor din magneziu, dacă fotonul cu cea mai mare lungime de undă care poate ejecta electroni este de 337 nm?
- Calculați energia de legătură în eV a electronilor din aluminiu, dacă fotonul cu cea mai mare lungime de undă care îi poate ejecta este de 304 nm.
- Care este energia cinetică maximă în eV a electronilor ejectați din metalul de sodiu de către radiația EM de 450 nm, având în vedere că energia de legătură este de 2,28 eV?
- Radiația UV cu lungimea de undă de 120 nm cade pe metalul de aur, la care electronii sunt legați cu 4,82 eV. Care este energia cinetică maximă a fotoelectronilor ejectați?
- Lumina violetă cu lungimea de undă de 400 nm ejectează electroni cu o energie cinetică maximă de 0,860 eV din metalul de sodiu. Care este energia de legătură a electronilor cu metalul de sodiu?
- Radiația UV cu lungimea de undă de 300 nm cade pe metalul de uraniu, proiectând electroni de 0,500 eV. Care este energia de legătură a electronilor cu uraniul metalic?
- (a) Care este lungimea de undă a radiației EM care ejectează electroni de 2,00-eV din metalul calciu, având în vedere că energia de legătură este de 2,71 eV? (b) Ce tip de radiație EM este aceasta?
- Căutați lungimea de undă a fotonilor care ejectează electroni de 0,100-eV din potasiu, având în vedere că energia de legătură este de 2,24 eV. Sunt acești fotoni vizibili?
- Care este viteza maximă a electronilor ejectați dintr-un material de către fotoni de 80 nm, dacă aceștia sunt legați de material cu 4,73 eV?
- Fotoelectronii dintr-un material cu o energie de legătură de 2,71 eV sunt ejectați de către fotoni de 420 nm. Odată ejectați, cât timp le ia acestor electroni să parcurgă 2,50 cm până la un dispozitiv de detecție?
- Un laser cu o putere de ieșire de 2,00 mW la o lungime de undă de 400 nm este proiectat pe calciu metalic. (a) Câți electroni pe secundă sunt ejectați? (b) Ce putere este antrenată de electroni, având în vedere că energia de legătură este de 2,71 eV?
- (a) Calculați numărul de fotoelectroni pe secundă ejectați de pe o suprafață de 1,00 mm 2 de metal de sodiu de către o radiație EM de 500 nm cu o intensitate de 1,30 kW/m2 (intensitatea luminii solare deasupra atmosferei terestre). (b) Având în vedere că energia de legătură este de 2,28 eV, ce putere este antrenată de electroni? (c) Electronii transportă mai puțină energie decât cea adusă de fotoni. Unde se duce cealaltă energie? Cum poate fi recuperată?
- Rezultate nerezonabile. Lumina roșie având lungimea de undă de 700 nm este proiectată asupra magneziului metalic la care electronii sunt legați cu 3,68 eV. (a) Folosiți KEe = hf – BE pentru a calcula energia cinetică a electronilor ejectați. (b) Ce este nerezonabil la acest rezultat? (c) Ce ipoteze sunt nerezonabile sau incoerente?
- Rezultate nerezonabile. (a) Care este energia de legătură a electronilor cu un material din care electronii de 4,00-eV sunt ejectați de o radiație EM de 400 nm? (b) Ce este nerezonabil în acest rezultat? (c) Ce ipoteze sunt nerezonabile sau incoerente?
Glosar
efectul fotoelectric: fenomenul prin care unele materiale ejectează electroni atunci când sunt luminate
foton: cuantă sau particulă de radiație electromagnetică
energie fotonică: cantitatea de energie pe care o are un foton; E = hf
energia de legare: numită și funcția de lucru; cantitatea de energie necesară pentru a ejecta un electron dintr-un material
Soluții alese la probleme & Exerciții
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
7. 2,25 eV
9. (a) 264 nm; (b) Ultraviolet
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) Energie cinetică negativă; (c) Faptul că electronii ar fi fost eliberați.
.
