Știință > Fizică > Efectul fotoelectric >Ecuația fotoelectrică a lui Einstein
În acest articol, vom deriva ecuația fotoelectrică a lui Einstein și vom studia utilizarea ei pentru a verifica caracteristicile efectului fotoelectric al luminii.
Natura ondulatorie a luminii:
Cristian Huygen a propus că lumina se propagă sub forma unei unde. Dar această teorie are un dezavantaj serios. Ea nu a fost capabilă să explice propagarea luminii în vid. Acest inconvenient a fost înlăturat de Maxwell care a propus că lumina este o undă electromagnetică și pentru propagarea undelor electromagnetice nu este necesar un mediu material. Astfel a fost stabilită natura ondulatorie a luminii.
Teoria undelor a fost capabilă să explice toate fenomenele asociate cu propagarea luminii. Dar nu a reușit să explice distribuția energiei și fenomenele moderne precum efectul fotoelectric, efectul Crompton etc.
Natura de particulă a luminii:
Max Planck a demonstrat că propagarea luminii sau a energiei are loc sub formă de pachete de energie numite cuante. Cuanta de lumină se numește foton și astfel a stabilit natura de particulă a luminii. Folosind natura particulară sau cuantică a radiației putem explica fenomenul efectului fotoelectric și efectul Crompton.
Teoria cuantică a lui Planck:
Teoria cuantică a fost propusă de Max Planck. Conform acestei teorii, radiația de la o sursă nu este emisă continuu, ci este emisă în pachete sau fascicule de energie. Aceste pachete se numesc cuante sau fotoni. Dacă radiația are frecvența ν, fiecare cuantă are energie, unde h este constanta lui Planck.
Atunci energia fotonului = E = hν
Energia este emisă în mod discontinuu. Acest lucru este contrar teoriei clasice care presupune că emisia de energie este un proces continuu.
Natura de particulă a radiațiilor electromagnetice:
Îninteracțiunea radiației cu materia, radiația se comportă ca și cum ar fi alcătuită din particule. Aceste particule se numesc fotoni. Fiecare foton are o energie care este dată de
E = hν = hc/λ
Toți fotonii de lumină de o anumită frecvență (lungime de undă) au aceeași cantitate de energie asociată cu ei. Creșterea intensității luminii mărește numărul de fotoni pe secundă care traversează o anumită suprafață, dar energia fiecărui foton va fi aceeași. Fotonii sunt neutri din punct de vedere electric și nu sunt afectați de câmpuri electrice sau magnetice. Fotonii se deplasează în linie dreaptă cu viteza luminii „c”, dar prezintă difracție în anumite condiții.
Primul moment al fiecărui foton este dat de
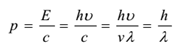
Lungimea de undă a fotonului se modifică în funcție de mediu, de aceea ei au viteze diferite în medii diferite. Masa de repaus a unui foton este zero. Masa sa cinetică este dată de
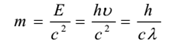
În coliziunea dintre fotoni și particule (cum ar fi coliziunea foton-electron), energia totală și impulsul se conservă. Cu toate acestea, este posibil ca numărul de fotoni să nu fie conservat într-o coliziune. Fotonul poate fi absorbit sau poate fi creat un nou foton.
Ecuația fotoelectrică a lui Einstein:
Pe baza teoriei cuantice a lui Planck, Einstein a derivat o ecuație pentru efectul fotoelectricei cunoscută sub numele de ecuația fotoelectrică a lui Einstein. Einstein a presupus că
- Lumina este formată din fotoni sau cuante de energie, energia din fiecare foton este hν. Unde h este constanta lui Planck și ν este frecvența luminii
- Care foton incident se ciocnește cu un electron din interiorul unui atom și cedează toată energia sa electronului.
- O parte din această energie este folosită de electron pentru a ieși de pe suprafața metalului, iar partea rămasă este energia cinetică cu care este emis electronul.
- Energia minimă necesară unui electron pentru a ieși de pe suprafața metalului se numește funcția de lucru fotoelectric (∅o) a metalului.
- Energia rămasă (hν – ∅o) este energia cinetică maximă a electronului cu care va fi ejectat un fotoelectron.
Astfel, Energia cinetică maximă a electronului = energia fotonului – funcția de lucru
Să fie „m” masa electronului și vmax viteza maximă a fotoelectronului cu care acesta va fi ejectat.

Această ecuație este cunoscută sub numele de ecuația fotoelectrică a lui Einstein
Funcția de lucru fotoelectric:
În efectul fotoelectric, electronul cel mai slab atașat de un atom de material fotosensibil este eliminat. Energia minimă necesară pentru a elibera un electron de pe o suprafață dată se numește funcția de lucru fotoelectric (∅o) a materialului suprafeței respective. Funcția de lucru este o proprietate caracteristică a suprafeței metalice.
Matematic, funcția de lucru este dată de
∅o = h νo
Unde νo = frecvența de prag și h =constanta lui Planck.
Explicarea existenței frecvenței de prag pe baza ecuației fotoelectrice a lui Einstein:
Pentru o anumită suprafață metalică, fotoelectronii sunt emiși numai atunci când frecvența luminii incidente este mai mare sau egală cu o anumită frecvență minimă (no)cunoscută sub numele de frecvență de prag. Frecvența de prag este diferită pentrudiferite substanțe,
Pe baza ecuației fotoelectrice a lui Einstein

Unde νo = frecvența de pragși h = constanta lui Planck și
ν = frecvența radiației incidente
Energia cinetică este întotdeauna o mărime nenegativă i.adică poate fi fie pozitivă, fie zero, astfel

Ceea ce indică faptul că, pentru efectul fotoelectric, frecvența radiației incidente sau a fotonului incident trebuie să fie egală sau mai mare decât frecvența de prag. Forța de atracție care acționează asupra fotoelectronilor probabili în diferiți atomi este diferită. Prin urmare, frecvența de prag este diferită pentru diferite substanțe.
Explicarea efectului intensității pe baza ecuației fotoelectrice a lui Einstein:
Dacă frecvența luminii incidente este mai mică decât frecvența de prag,fotoelectronii nu sunt emiși, oricât de mare ar fi intensitatea luminii incidente.
Numărul de fotoelectroni emiși pe secundă este direct proporțional cu intensitatea luminii incidente. Astfel, curentul fotoelectric este directproporțional cu intensitatea luminii incidente. Dacă intensitatea luminii este mai mare, numărul de fotoni incidente pe suprafață este mai mare. Datorită numărului mai mare de fotoelectroni, rata de fotoemisiune crește, ceea ce face ca intensitatea curentului fotoelectric să crească. Astfel, putem concluziona că efectul (curentul) fotoelectric este direct proporțional cu intensitatea radiației incidente.
Explicarea energiei cinetice maxime posibile pe baza ecuației fotoelectrice a lui Einstein:
Pe baza ecuației fotoelectrice a lui Einstein

Unde νo = frecvența de pragși h = constanta lui Planck și
ν = frecvența radiației incidente
această ecuație nu conține termenul de intensitate, astfel putem spune că energia cinetică maximă a fotoelectronului este independentă de intensitatea radiației incidente, dar depinde de frecvența radiației incidente. Această ecuație indică faptul că energia cinetică maximă a electronului depinde de frecvența radiației incidente. Și dacă frecvența radiației incidente crește, energia cinetică a fotoelectronului crește și ea.
Explicarea instantaneității efectului fotoelectric pe baza ecuației fotoelectrice a lui Einstein:
Efectul fotoelectric este un proces instantaneu. Nu există un decalaj de timp între incidența luminii și emisia de fotoelectroni, cu alte cuvinte, suprafața începe să emită fotoelectroni imediat ce lumina cade pe ea. De asemenea, emisia de foto-electroni se oprește în momentul în care lumina incidentă este întreruptă.
Când radiația este incidentă pe suprafața fotoemisoare în acel moment, întreaga energie a fotonului este transferată unui singur electron dintr-o singură dată. Astfel, electronul este emis fără nici un decalaj de timp, iar efectul fotoelectric este procesul instantaneu.
Subiectul anterior: Probleme numerice privind efectul fotoelectric
Subiectul următor: Efectul fotoelectric: Probleme numerice privind ecuația fotoelectrică
Știință > Fizică > Efectul fotoelectric >Ecuația fotoelectrică a lui Einstein
.
