Prueba de Wald: Definición, ejemplos, ejecución de la prueba

Pruebas de hipótesis > Prueba de Wald

¿Qué es la prueba de Wald?

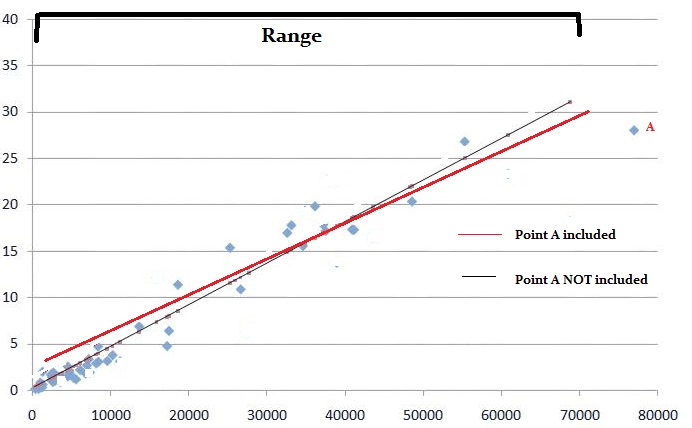
La prueba de Wald puede indicarle qué variables del modelo están aportando algo significativo.

La prueba de Wald (también llamada prueba de Chi-Cuadrado de Wald) es una forma de averiguar si las variables explicativas de un modelo son significativas. «Significativo» significa que añaden algo al modelo; las variables que no añaden nada pueden eliminarse sin afectar al modelo de forma significativa. La prueba puede utilizarse para una multitud de modelos diferentes, incluidos aquellos con variables binarias o continuas.
La hipótesis nula para la prueba es: algún parámetro = algún valor. Por ejemplo, podría estar estudiando si el peso se ve afectado por comer comida basura dos veces por semana. «Peso» sería su parámetro. El valor podría ser cero (indicando que no crees que el peso se ve afectado por comer comida basura). Si se rechaza la hipótesis nula, sugiere que las variables en cuestión pueden ser eliminadas sin mucho daño para el ajuste del modelo.

• Si la prueba de Wald muestra que los parámetros de ciertas variables explicativas son cero, puede eliminar las variables del modelo.
• Si la prueba muestra que los parámetros no son cero, debe incluir las variables en el modelo.

Se suele hablar de la prueba de Wald en términos de chi-cuadrado, porque la distribución de muestreo (a medida que n se acerca al infinito) suele ser conocida. Esta variante de la prueba se denomina a veces prueba de chi-cuadrado de Wald para diferenciarla de la prueba de chi-cuadrado logarítmica de Wald, que es una variante no paramétrica basada en los logaritmos de las probabilidades.

Comparación con otras pruebas

La prueba de Wald es una aproximación a la prueba de razón de verosimilitud. Sin embargo, se puede ejecutar con un solo modelo (la prueba LR requiere al menos dos). También es más ampliamente aplicable que la LRT: a menudo, se puede ejecutar un Wald en situaciones en las que no se puede ejecutar ninguna otra prueba.

Para valores grandes de n, la prueba de Wald es aproximadamente equivalente a la prueba t; ambas pruebas rechazarán los mismos valores para tamaños de muestra grandes. Las pruebas de Wald, LRT y del multiplicador de Lagrange son todas equivalentes a medida que el tamaño de las muestras se acerca al infinito (lo que se denomina «asintóticamente equivalente»). Sin embargo, es probable que las muestras de tamaño finito, especialmente las más pequeñas, den resultados muy diferentes.

Agresti (1990) sugiere que se utilice la LRT en lugar de la prueba de Wald para tamaños de muestra pequeños o si los parámetros son grandes. Un tamaño de muestra «pequeño» es inferior a unos 30.

Ejecución de la prueba

¿Necesita ayuda con una pregunta de los deberes? Consulte nuestra página de tutorías.

La fórmula del test de Wald es: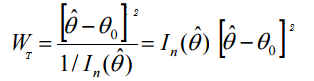

Donde:

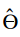• = Estimador de Máxima Verosimilitud (MLE),
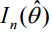• = información esperada de Fisher (evaluada en el MLE).

Básicamente, el test busca diferencias: Θ0 – Θ. Los pasos generales son:

1. Encontrar el MLE.
2. Encontrar la información de Fisher esperada.
3. Evaluar la información de Fisher en el MLE.

Con la combinación del MLE y la información de Fisher, la prueba de Wald es muy compleja de trabajar y no se suele calcular a mano. Muchas aplicaciones de software pueden ejecutar la prueba.

• Stata: use el comando test.
• R: vea las instrucciones de la prueba WALD para R (descargue un PDF) de la Universidad de Toronto.
• SAS: use la sentencia TEST. WALD es el valor por defecto si no se especifica ninguna prueba.

Referencia:
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, New York.

——————————————————————————

¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!