
Pitágoras de Samos (c.570-495 A.C.)
Biografía – Quién fue Pitágoras
A veces se afirma que debemos las matemáticas puras a Pitágoras, y a menudo se le llama el primer «verdadero» matemático. Pero, aunque su contribución fue claramente importante, sigue siendo una figura controvertida.
No dejó escritos matemáticos, y gran parte de lo que sabemos sobre el pensamiento pitagórico nos llega a través de los escritos de Filolao y otros eruditos pitagóricos posteriores. De hecho, no está nada claro si muchos (o ninguno) de los teoremas que se le atribuyen fueron resueltos por Pitágoras personalmente o por sus seguidores.
La escuela que estableció en Croton, en el sur de Italia, alrededor del año 530 a.C., fue el núcleo de una secta pitagórica bastante extraña. Aunque el pensamiento pitagórico estaba dominado en gran medida por las matemáticas, también era profundamente místico, y Pitágoras impuso sus filosofías casi religiosas, el vegetarianismo estricto, la vida en común, los ritos secretos y las reglas extrañas a todos los miembros de su escuela (incluyendo edictos extraños y aparentemente aleatorios sobre no orinar nunca hacia el sol, no casarse nunca con una mujer que lleve joyas de oro, no pasar nunca por delante de un asno tumbado en la calle, no comer ni tocar nunca las habas negras, etc) .
Los miembros se dividían en los «mathematikoi» (o «aprendices»), que ampliaban y desarrollaban el trabajo más matemático y científico que inició el propio Pitágoras, y los «akousmatikoi» (o «oyentes»), que se centraban en los aspectos más religiosos y rituales de sus enseñanzas. Siempre hubo una cierta fricción entre los dos grupos y, finalmente, la secta se vio envuelta en una feroz lucha local y acabó dispersándose. El resentimiento contra el secretismo y la exclusividad de los pitagóricos creció y, en el año 460 a.C., todos sus lugares de reunión fueron quemados y destruidos, y al menos 50 miembros fueron asesinados sólo en Croton.
La máxima de la escuela de Pitágoras era «Todo es número» o «Dios es número», y los pitagóricos practicaban efectivamente una especie de numerología o culto a los números, y consideraban que cada número tenía su propio carácter y significado. Por ejemplo, el número uno era el generador de todos los números; el dos representaba la opinión; el tres, la armonía; el cuatro, la justicia; el cinco, el matrimonio; el seis, la creación; el siete, los siete planetas o «estrellas errantes»; etc. Los números impares se consideraban femeninos y los pares masculinos.
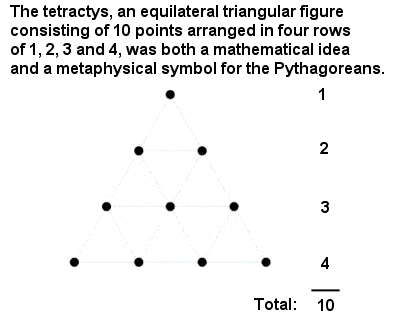
La Tetractys pitagórica
El número más sagrado de todos era la «Tetractys» o decena, un número triangular compuesto por la suma de uno, dos, tres y cuatro. Es un gran tributo a los logros intelectuales de los pitagóricos el hecho de que dedujeran el lugar especial del número 10 a partir de un argumento matemático abstracto y no de algo tan mundano como contar los dedos de las dos manos.
Sin embargo, Pitágoras y su escuela -así como un puñado de otros matemáticos de la antigua Grecia- fue en gran medida responsable de la introducción de una matemática más rigurosa que la anterior, construyendo a partir de los primeros principios utilizando axiomas y lógica. Antes de Pitágoras, por ejemplo, la geometría había sido una mera colección de reglas derivadas de la medición empírica.
Pitágoras descubrió que se podía construir un sistema completo de matemáticas, en el que los elementos geométricos se correspondían con los números, y en el que los enteros y sus proporciones eran todo lo necesario para establecer todo un sistema de lógica y verdad.
El Teorema de Pitágoras
Se le recuerda principalmente por lo que se ha conocido como el Teorema de Pitágoras (o el Teorema de Pitágoras): que, para cualquier triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado más largo, opuesto al ángulo recto) es igual a la suma del cuadrado de los otros dos lados (o «catetos»).
Escrito como una ecuación: a2 + b2 = c2.
Lo que Pitágoras y sus seguidores no se dieron cuenta es que esto también funciona para cualquier forma: así, el área de un pentágono en la hipotenusa es igual a la suma de los pentágonos de los otros dos lados, al igual que para un semicírculo o cualquier otra forma regular (o incluso irregular(.
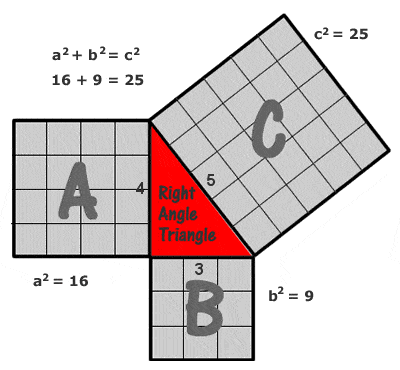
Teorema de Pitágoras
El ejemplo más sencillo y más citado de triángulo pitagórico es uno con lados de 3, 4 y 5 unidades (32 + 42 = 52, como puede verse dibujando una cuadrícula de cuadrados unitarios en cada lado como en el diagrama de la derecha), pero hay un número potencialmente infinito de otros «triángulos pitagóricos» enteros, empezando por (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. Hay que señalar, sin embargo, que (6, 8, 10) no es lo que se conoce como un triple pitagórico «primitivo», ya que no es más que un múltiplo de (3, 4, 5).
El Teorema de Pitágoras y las propiedades de los triángulos rectángulos parece ser el desarrollo matemático más antiguo y extendido después de la aritmética y la geometría básicas, y fue tocado en algunos de los textos matemáticos más antiguos de Babilonia y Egipto, que datan de más de mil años antes. Una de las pruebas más sencillas procede de la antigua China, y probablemente data de mucho antes del nacimiento de Pitágoras. Sin embargo, fue Pitágoras quien dio al teorema su forma definitiva, aunque no está claro si el propio Pitágoras lo demostró definitivamente o simplemente lo describió. En cualquier caso, se ha convertido en uno de los teoremas matemáticos más conocidos, y en la actualidad existen hasta 400 demostraciones diferentes, algunas geométricas, otras algebraicas, otras que implican ecuaciones diferenciales avanzadas, etc.
Pronto se hizo evidente, sin embargo, que también eran posibles soluciones no enteras, de modo que un triángulo isósceles con lados 1, 1 y √2, por ejemplo, también tiene un ángulo recto, como los babilonios habían descubierto siglos antes. Sin embargo, cuando el alumno de Pitágoras, Hipaso, intentó calcular el valor de √2, descubrió que no era posible expresarlo como una fracción, indicando así la existencia potencial de todo un nuevo mundo de números, los números irracionales (números que no pueden expresarse como simples fracciones de enteros). Este descubrimiento destrozó bastante el elegante mundo matemático construido por Pitágoras y sus seguidores, y la existencia de un número que no podía expresarse como el cociente de dos creaciones de Dios (que es como pensaban en los enteros) puso en peligro todo el sistema de creencias del culto.
El pobre Hipaso fue aparentemente ahogado por los reservados pitagóricos por difundir este importante descubrimiento al mundo exterior. Pero la sustitución de la idea de la divinidad de los enteros por el concepto más rico del continuo, fue un desarrollo esencial en las matemáticas. Marcó el verdadero nacimiento de la geometría griega, que se ocupa de líneas y planos y ángulos, todos ellos continuos y no discretos.
Entre sus otros logros en geometría, Pitágoras (o al menos sus seguidores, los pitagóricos) también se dio cuenta de que la suma de los ángulos de un triángulo es igual a dos ángulos rectos (180°), y probablemente también la generalización que afirma que la suma de los ángulos interiores de un polígono con n lados es igual a (2n – 4) ángulos rectos, y que la suma de sus ángulos exteriores es igual a 4 ángulos rectos. Fueron capaces de construir figuras de un área determinada, y de utilizar el álgebra geométrica simple, por ejemplo para resolver ecuaciones como a(a – x) = x2 por medios geométricos.
Los pitagóricos también establecieron los fundamentos de la teoría de los números, con sus investigaciones sobre los números triangulares, cuadrados y también perfectos (números que son la suma de sus divisores). Descubrieron varias propiedades nuevas de los números cuadrados, como que el cuadrado de un número n es igual a la suma de los n primeros números impares (por ejemplo, 42 = 16 = 1 + 3 + 5 + 7). También descubrieron al menos el primer par de números amigables, 220 y 284 (los números amigables son pares de números para los que la suma de los divisores de un número es igual al otro número, por ejemplo, los divisores propios de 220 son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, cuya suma es 284; y los divisores propios de 284 son 1, 2, 4, 71 y 142, cuya suma es 220).
Teoría de la música
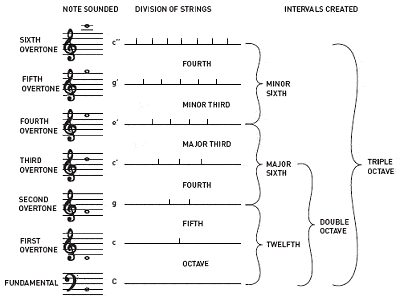
Se atribuye a Pitágoras el descubrimiento de las relaciones entre los tonos musicales armoniosos
También se atribuye a Pitágoras el descubrimiento de que los intervalos entre las notas musicales armoniosas tienen siempre relaciones de números enteros. Por ejemplo, al tocar la mitad de una cuerda de guitarra se obtiene la misma nota que la cuerda abierta, pero una octava más alta; un tercio de una longitud da una nota diferente pero armoniosa; etc.
Las relaciones de números no enteros, por el contrario, tienden a dar sonidos disonantes. De este modo, Pitágoras describió los cuatro primeros sobretonos que crean los intervalos comunes que se han convertido en los principales bloques de construcción de la armonía musical: la octava (1:1), la quinta perfecta (3:2), la cuarta perfecta (4:3) y la tercera mayor (5:4). La forma más antigua de afinar la escala cromática de 12 notas se conoce como afinación pitagórica, y se basa en una pila de quintas perfectas, cada una de ellas afinada en la proporción 3:2.
El místico Pitágoras se entusiasmó tanto con este descubrimiento que se convenció de que todo el universo se basaba en números, y que los planetas y las estrellas se movían según ecuaciones matemáticas, que se correspondían con notas musicales, y así produjo una especie de sinfonía, la «Musical Universalis» o «Música de las Esferas».
| << Volver a las matemáticas griegas | Adelante con Platón >> |
